Assertion : The field strength at the centre of a ring is zero
Reason : At the centre of the ring, slope of V-r graph is zero.\
If both Assertin and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:A
To solve the question, we need to analyze the assertion and the reason provided.
1. Understanding the Assertion:
The assertion states that "The field strength at the center of a ring is zero."
- A ring of mass exerts gravitational force on a point located at its center. Due to symmetry, the gravitational forces exerted by all the mass elements of the ring cancel each other out at the center. Therefore, the net gravitational field strength at the center of the ring is indeed zero.
2. Understanding the Reason:
The reason states that "At the center of the ring, the slope of the V-r graph is zero."
- In gravitational terms, V represents the gravitational potential, and r represents the distance from the center of the ring. The gravitational field strength (E) is related to the gravitational potential (V) by the equation:
E=−dVdr
- If the gravitational field strength (E) is zero (as established in the assertion), then:
E=0⟹−dVdr=0⟹dVdr=0
- This means that the slope of the V-r graph, which represents the rate of change of gravitational potential with respect to distance, is indeed zero at the center of the ring.
3. Conclusion:
- Since both the assertion and the reason are true, and the reason correctly explains the assertion, we can conclude that both statements are valid.
Final Answer:
- The assertion is true, and the reason is also true, with the reason correctly explaining the assertion.
The assertion states that "The field strength at the center of a ring is zero."
- A ring of mass exerts gravitational force on a point located at its center. Due to symmetry, the gravitational forces exerted by all the mass elements of the ring cancel each other out at the center. Therefore, the net gravitational field strength at the center of the ring is indeed zero.
The reason states that "At the center of the ring, the slope of the V-r graph is zero."
- In gravitational terms, V represents the gravitational potential, and r represents the distance from the center of the ring. The gravitational field strength (E) is related to the gravitational potential (V) by the equation:
E=−dVdr
- If the gravitational field strength (E) is zero (as established in the assertion), then:
E=0⟹−dVdr=0⟹dVdr=0
- This means that the slope of the V-r graph, which represents the rate of change of gravitational potential with respect to distance, is indeed zero at the center of the ring.
- Since both the assertion and the reason are true, and the reason correctly explains the assertion, we can conclude that both statements are valid.
- The assertion is true, and the reason is also true, with the reason correctly explaining the assertion.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionAssertion : Half of the ring is uniformly positively charged and other half uniformly negatively charged. Then, electric field is zero at centre. Then , electric field is zero at centre.
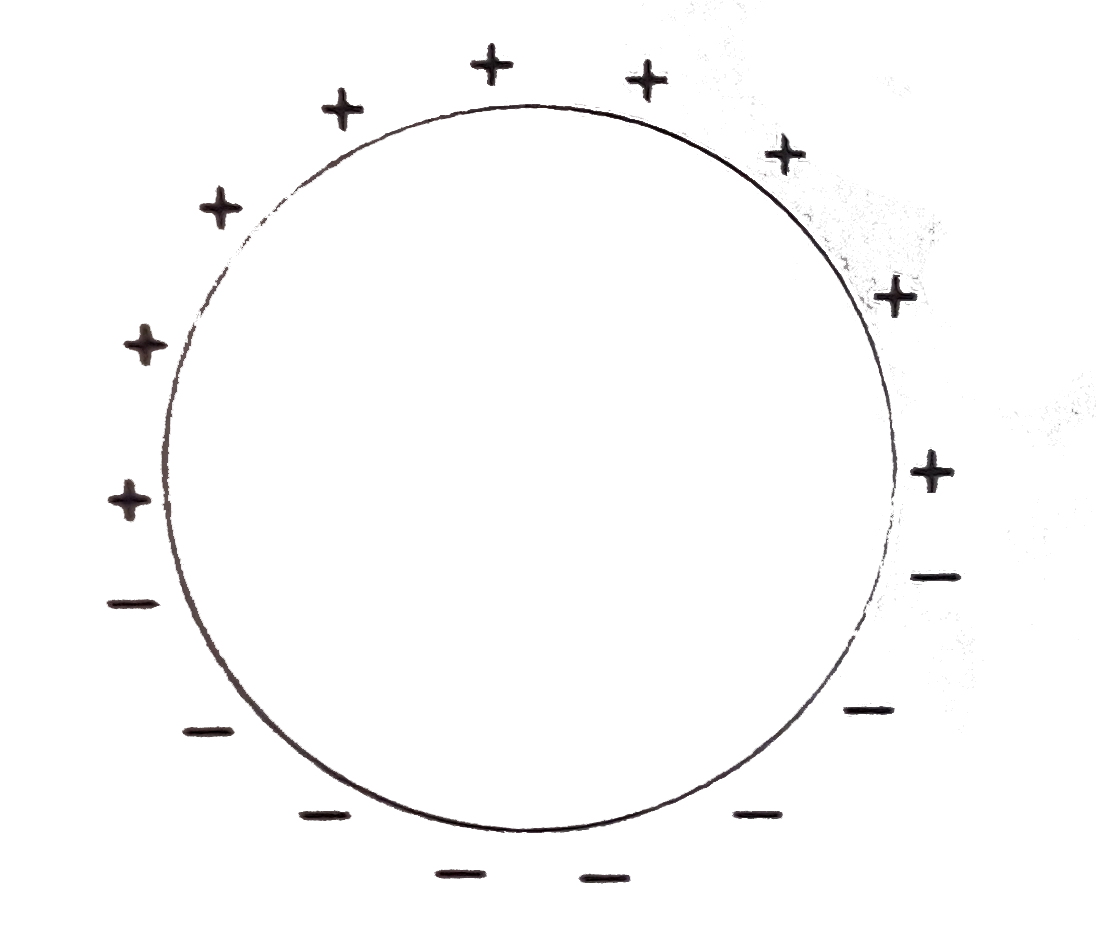
Reason : At the centre of uniformly charged ring, electric field is zero. 1)If both Assertion and Reason are correct and Reason is the correct explanation of Assertion 2)If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion 3)If Assertion is true but Reason is false 4)If Assertion is false but Reason is true
View Solution
Knowledge Check
A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A : If an object is taken to the centre of earth, then its centre of gravity cannot be defined.
R : At the centre of earth acceleration due to gravity is zero.
View SolutionAssertion : If we plot potential versus x- coordinate graph along the x-axis, then field strength is zero where slope of V−x graph is zero.
Reason : If potential is function of x- only then
E=−dVdx
View SolutionCentre of mass of a ring will be at a position:
View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
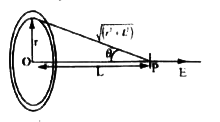
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionAssertion : Electric field outside the conducting wire which carreis a constant is zero.
Reason : Net charge on conducting wire is zero.
View Solution
