The Gauss' theorem for gravitational field may be written as
∮g⋅dS=mG
−∮g⋅dS=4πmG
∮g⋅dS=m4πG
−∮g⋅dS=mG
The correct Answer is:B
To rewrite Gauss' theorem for the gravitational field, we start by recalling the form of Gauss' theorem for electric fields and then adapt it to gravitational fields.
1. Understanding Gauss' Theorem for Electric Fields:
Gauss' theorem for electric fields states that:
∮E⋅ds=Qencϵ0
where E is the electric field, ds is a differential area vector on a closed surface, Qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
2. Comparing Electric and Gravitational Fields:
In the case of gravitational fields, we denote the gravitational field intensity as g and the mass enclosed as M. The gravitational field intensity due to a mass M at a distance r is given by:
g=GMr2
where G is the gravitational constant.
3. Rewriting Gauss' Theorem for Gravitational Fields:
By analogy, we can write Gauss' theorem for gravitational fields as:
∮g⋅ds=MencG
where Menc is the mass enclosed by the surface.
4. Relating to the Electric Field Equation:
From the electric field equation, we can relate the constants:
ϵ0=14πG
Thus, substituting this into our gravitational Gauss' theorem gives:
∮g⋅ds=4πGMenc
5. Including the Direction of Gravitational Field:
Since the gravitational field is always attractive, we include a negative sign to indicate this nature:
∮g⋅ds=−4πGMenc
Final Expression:
Thus, the Gauss' theorem for the gravitational field can be written as:
∮g⋅ds=−4πGMenc
Gauss' theorem for electric fields states that:
∮E⋅ds=Qencϵ0
where E is the electric field, ds is a differential area vector on a closed surface, Qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
In the case of gravitational fields, we denote the gravitational field intensity as g and the mass enclosed as M. The gravitational field intensity due to a mass M at a distance r is given by:
g=GMr2
where G is the gravitational constant.
By analogy, we can write Gauss' theorem for gravitational fields as:
∮g⋅ds=MencG
where Menc is the mass enclosed by the surface.
From the electric field equation, we can relate the constants:
ϵ0=14πG
Thus, substituting this into our gravitational Gauss' theorem gives:
∮g⋅ds=4πGMenc
Since the gravitational field is always attractive, we include a negative sign to indicate this nature:
∮g⋅ds=−4πGMenc
Thus, the Gauss' theorem for the gravitational field can be written as:
∮g⋅ds=−4πGMenc
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Assertion And Reason
11 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Gravitational field due to a solid sphere
View SolutionA particle of mass m and charge q is thrown from a point in space where uniform gravitational field & electric field are present.The particle
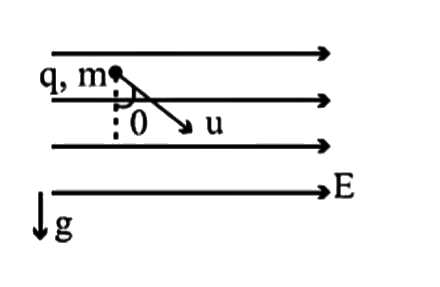
(1) may follow a straight line
( 2) may follow a circular path
( 3) may follow a parabolic apth
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionIf gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
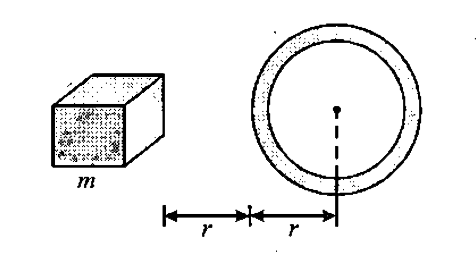
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View SolutionThe intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is 6N/kg. The gravitational potential at that point is -(in joule /kg)
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
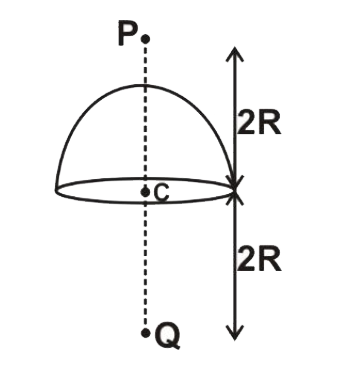
View SolutionIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
View SolutionA particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View SolutionFigure show a hemispherical shell having uniform mass density The direction of gravitational field at point P will be along
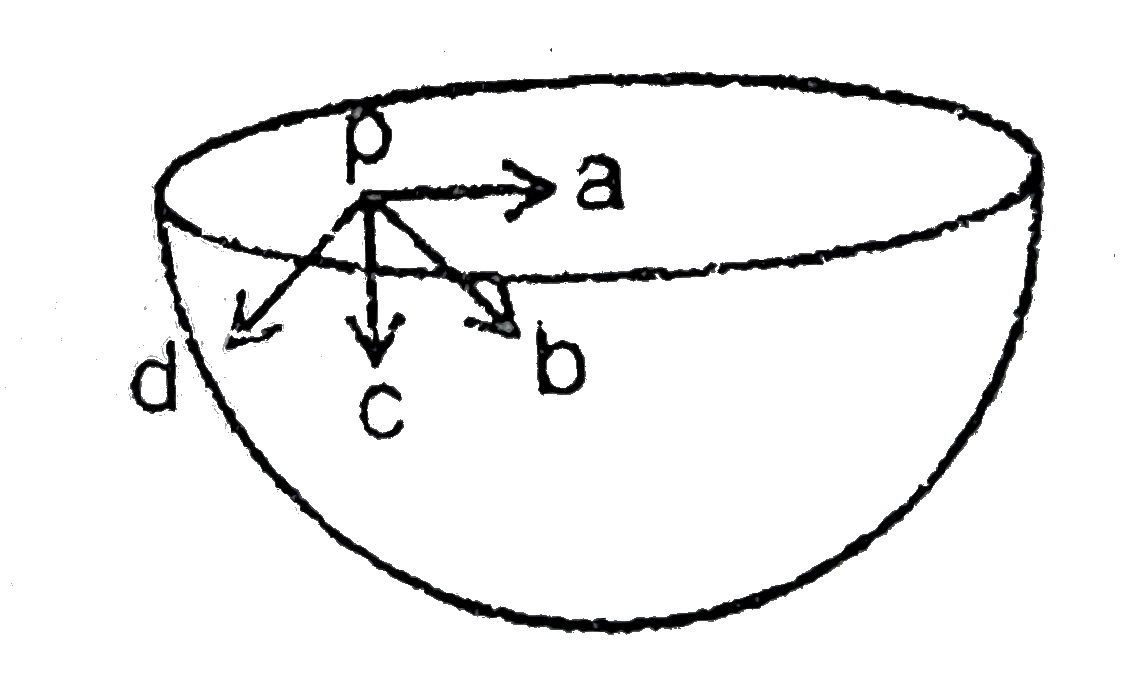 .
.
View Solution
