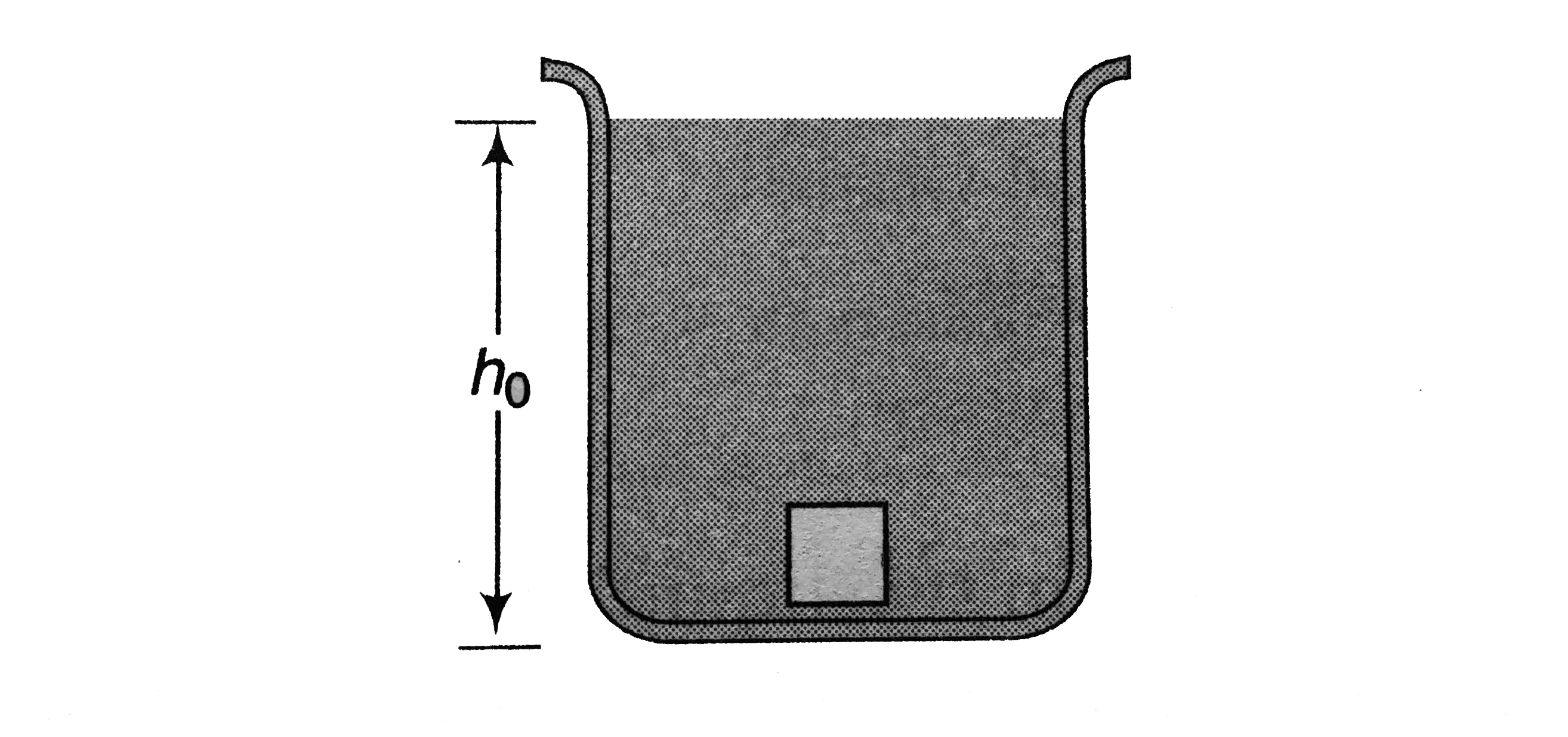
Figure shown a container having liquid of variable density. The density of liquid veriesas ρ=ρ0(4−3hh0). Here, h0 and ρ0 are constants and h is measured from bottom of the container. A solid block of small dimensions whose density is 52ρ0 and mass m is released from bottom of the tank. Prove that the block will execute simple harmonic motion. Find the frequency of oscillation.
 .
.
The correct Answer is:A, B
Net force on the block at a height h from the bottom is
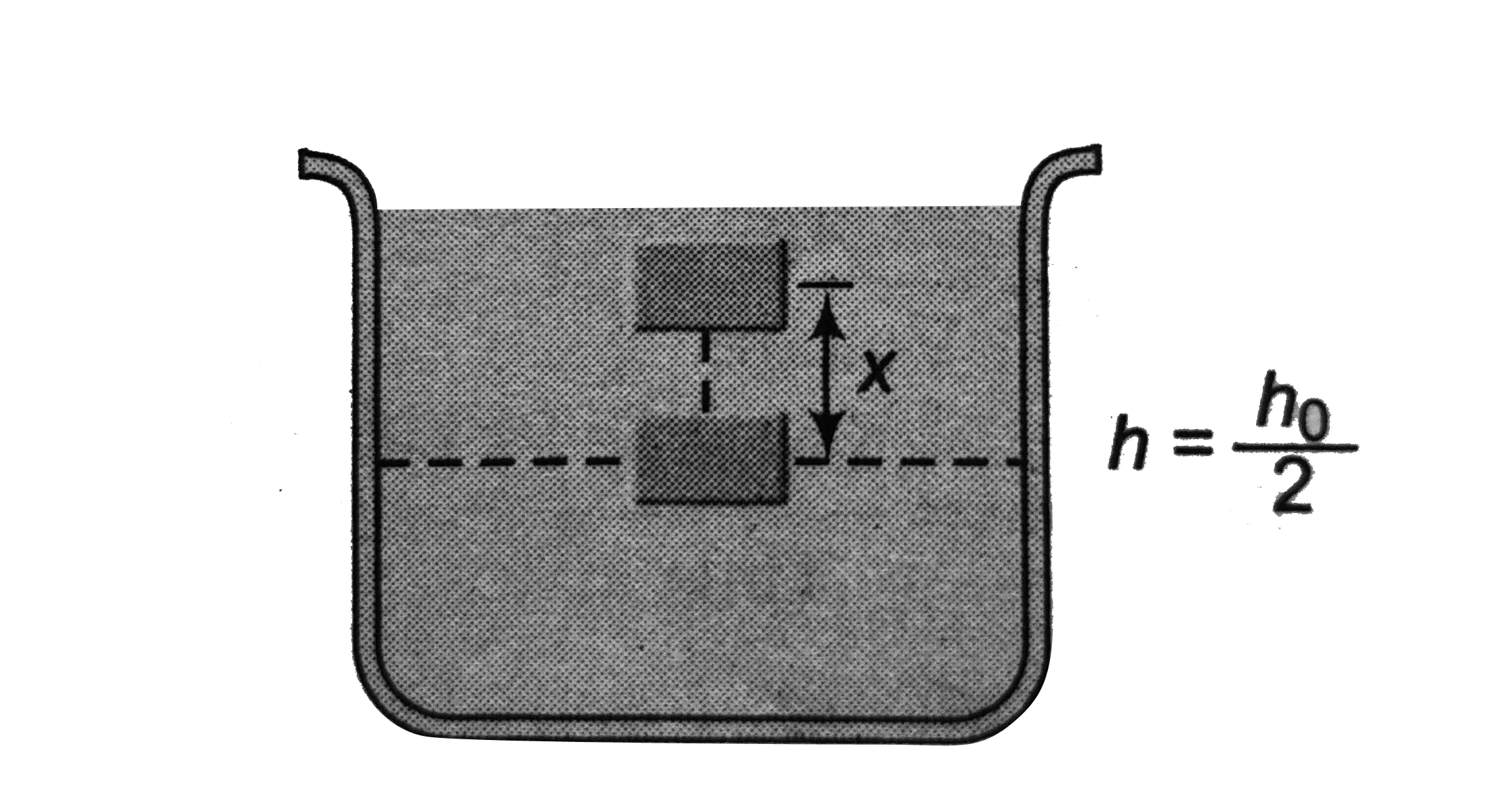
Fnet=upthrust-weight (upwards)
=⎛⎝m52ρ0⎞⎠ρ0(4−3hh0)g−mg
Fnet=0ath=h02
so, h=h02 is the equilibrium positive of the block.
For h>h02 weightgtuupthrust
i.e. net force is downwards and for h<h02
weight lt upthrust
i.e. net force is upwards
For upward displacement x from mean position, net downward force is
F=−⎡⎣⎛⎝m52ρ0⎞⎠ρ0{4−3(h−x)h0}g−mg⎤⎦(h=h02)
∴F=−6mg5h0x ....(i)
(because at h=h02 upthrust and weight are equal)
since, F∝−x
Oscillations are simple harmonic in nature Rewriting Eq. (i)
ma=−6mgx5h0
or, a=−6g5h0x
∴f=12π√∣∣ax∣∣
f=12π√6g5h0.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
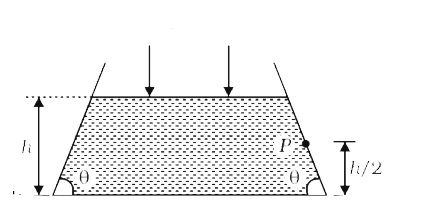
A container (see figure) contains a liquid upto a height h. The density of the liquid is The gauge pressure at point P is ρghx. Find the value of x
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
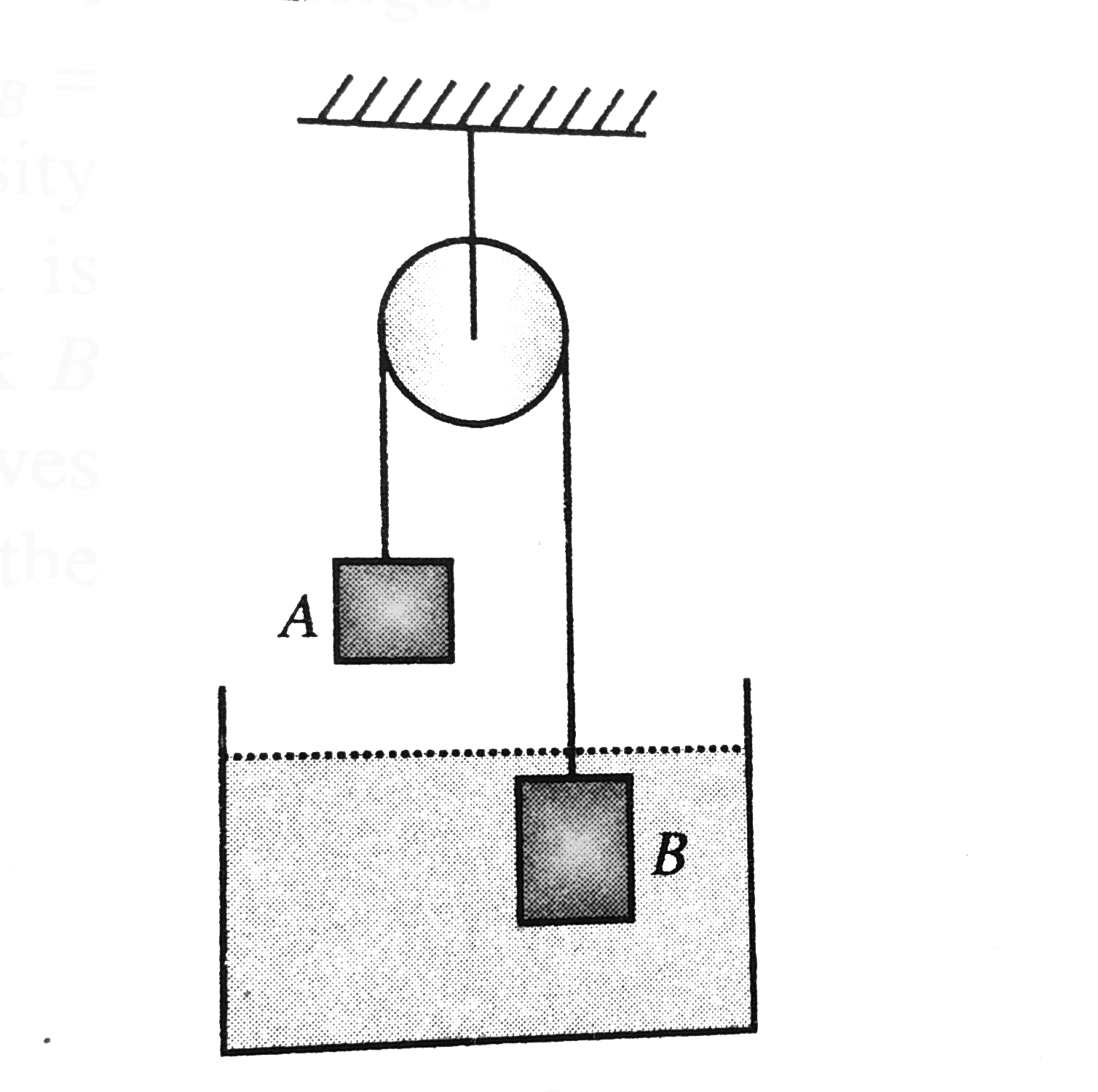
View SolutionIn the arrangement as shown, mB=3m, density of liquid is ρ and density of block B is 2ρ. The system is released from rest so that block B moves up when in liquid and moves down when out of liquid with the same acceleration. Find the mass of block A.
View SolutionA uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
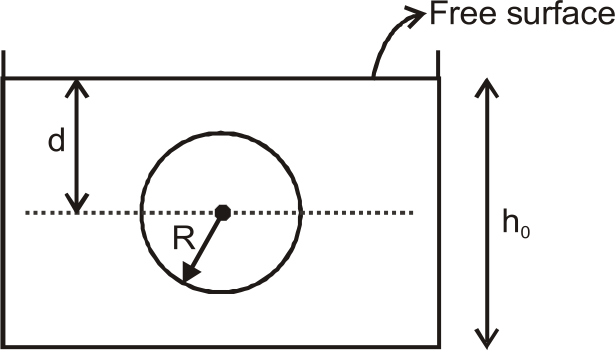
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View SolutionA ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
View Solution
