The shape of an ancient water clock jug is such that water level descends at a constant rate at all time. If the water level falls by 4cm every hour, determine the shape of the jar, i.e. specify x as a function of y. The radius of drain hole in 2mm and can be assumed to be very small compared to x.
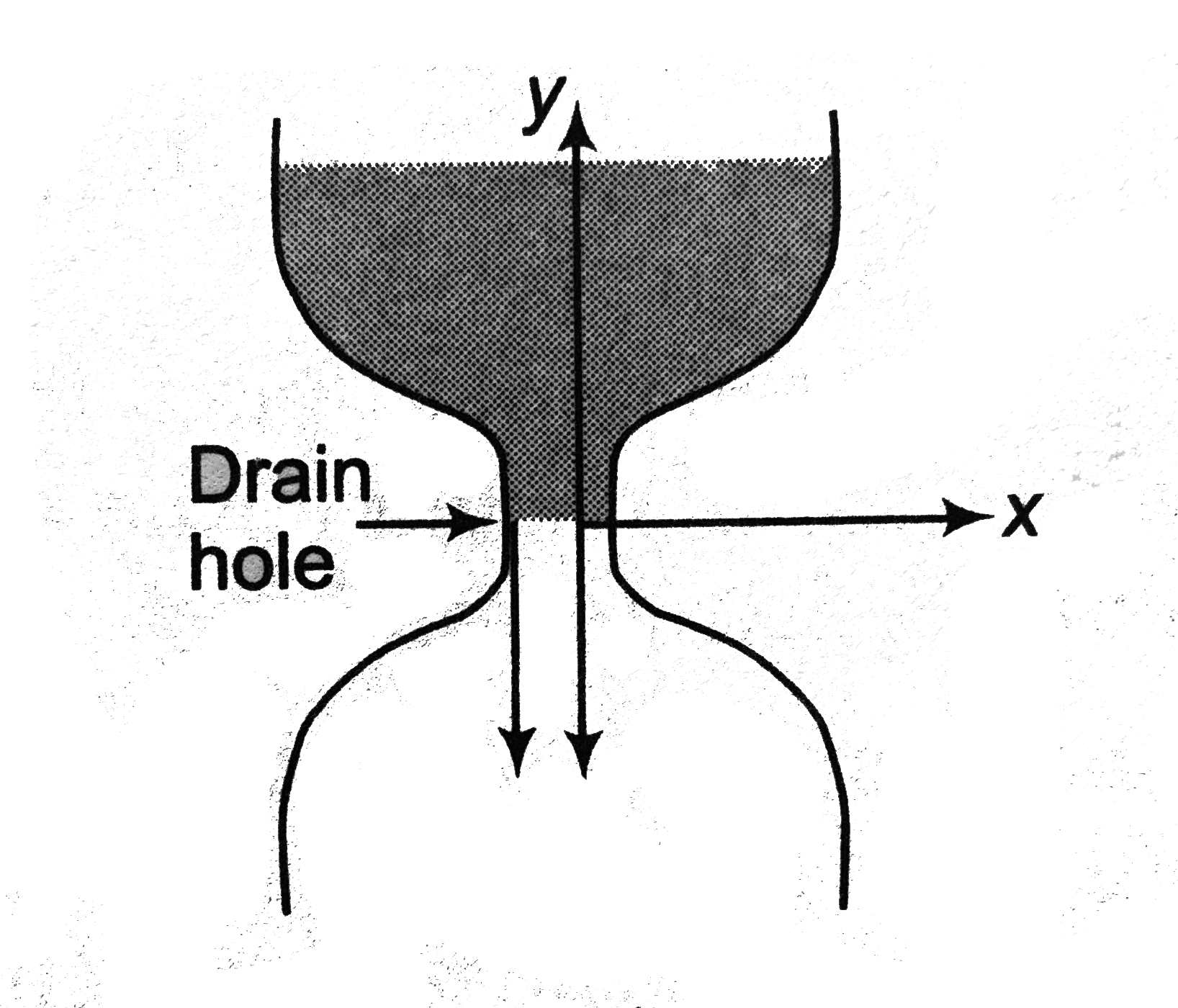
The correct Answer is:D
a√2gy=πx2(−dydt)
Here, −dydt=4×10−23600=1.11×10−5m/s
a=πr2=π(2×10−3)2
=1.26×10−5m2
substituting these values in Eq, (i) we have
(1.26×10−5)√2×9.8×y=π(1.11×10−5)x2
or, y=0.4x4
This is the desired x-y relation.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct36videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct10videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective36videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A vessel in the shape of a cuboid contains some water. If three indentical spheres are immersed in the water, the level of water is increased by 2cm. If the area of the base of the cuboid is 160 cm2 and its height 12cm, determine the radius of any of the spheres.
View SolutionA 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.
View SolutionIf the velocity of flow of water through a small hole is 0.6√2gy, where g is the acceleration due to gravity and y is the height of water level above the hole, find the time required to empty a tank having the shape of a right circular cone of base radius a and height h filled completely with water and having a hole of area A0 in the base.
View Solution_E01_079_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_079_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q. The wavefrot of a light beam is given by the equation x+2y+3z=c (where c is arbitrary constant) then the angle made by the direction of light with the y-axis isView SolutionPath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-View SolutionWater is drained from a vertical cylindrical tank by opening a valve at the base of the tank. It is known that the rate at which the water level drops is proportional to the square root of water depth y, where the constant of proportionality k>0 depends on the acceleration due to gravity and the geometry of the hole. If t is measured in minutes and k=115, then the time to drain the tank if the water is 4 m deep to start with is (a) 30 min (b) 45 min (c) 60 min (d) 80 min
View SolutionA water tank has the shape of an inverted righ circular cone with its axis vertical and vertex lowermost . Its semi-vertical angle is tan−1(0.5) . Water is poured into it at a constant rate of 4 cubic meter per hour . Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 2 m.
View SolutionA water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan−1(0.5). Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4m.
View SolutionWater is filled to a height of 2.5m in a container lying rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side √3 and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than 4×104 pascal
a, What minimum acceleration can be given to the container in the positive x-direction so that the cap will come out of the hole? Assume water does not spill out of container when the container accelerates.
Find the velocity of efflux as soon as the container starts moving with the acceleration calculated in part a. of the question.
 View Solution
View SolutionA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
if work function of the metal of the foil is 2.2 eV, the time taken by electron to come out is nearlyView Solution

