Four sources of sound each of sound level 10dB are sounded together in phase , the resultant intensity level will be (log102=0.3)
40dB
26dB
22dB
13dB
The correct Answer is:C
To solve the problem of finding the resultant intensity level when four sources of sound, each at a sound level of 10 dB, are sounded together in phase, we can follow these steps:
1. Understanding Sound Levels:
Each sound source has a sound level of 10 dB. The sound level in decibels (dB) is related to the intensity of sound.
2. Intensity Relationship:
The intensity level L in dB is given by the formula:
L=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity.
3. Calculating Intensity for One Source:
For one source at 10 dB:
10=10log10(I1I0)
Dividing both sides by 10:
1=log10(I1I0)
Therefore,
I1I0=10⇒I1=10I0
4. Calculating Total Intensity for Four Sources:
Since the sources are in phase, the intensities add up. Thus, the total intensity Itotal from four sources is:
Itotal=4I1=4×10I0=40I0
5. Finding Resultant Sound Level:
Now we can find the resultant sound level Ltotal:
Ltotal=10log10(ItotalI0)=10log10(40I0I0)=10log10(40)
6. Using Logarithm Properties:
We can express 40 as 10×4:
log10(40)=log10(10)+log10(4)=1+log10(4)
Using the approximation log10(4)=2log10(2) and given log10(2)=0.3:
log10(4)=2×0.3=0.6
Thus,
log10(40)=1+0.6=1.6
7. Calculating Final Sound Level:
Therefore,
Ltotal=10×1.6=16 dB
Since we need to add the original sound level of 10 dB:
Lfinal=10+16=26 dB
Final Answer:
The resultant intensity level when four sources of sound each at 10 dB are sounded together in phase is 26 dB.
Each sound source has a sound level of 10 dB. The sound level in decibels (dB) is related to the intensity of sound.
The intensity level L in dB is given by the formula:
L=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity.
For one source at 10 dB:
10=10log10(I1I0)
Dividing both sides by 10:
1=log10(I1I0)
Therefore,
I1I0=10⇒I1=10I0
Since the sources are in phase, the intensities add up. Thus, the total intensity Itotal from four sources is:
Itotal=4I1=4×10I0=40I0
Now we can find the resultant sound level Ltotal:
Ltotal=10log10(ItotalI0)=10log10(40I0I0)=10log10(40)
We can express 40 as 10×4:
log10(40)=log10(10)+log10(4)=1+log10(4)
Using the approximation log10(4)=2log10(2) and given log10(2)=0.3:
log10(4)=2×0.3=0.6
Thus,
log10(40)=1+0.6=1.6
Therefore,
Ltotal=10×1.6=16 dB
Since we need to add the original sound level of 10 dB:
Lfinal=10+16=26 dB
The resultant intensity level when four sources of sound each at 10 dB are sounded together in phase is 26 dB.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Subjective45videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Subjective Questions1videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Assertion And Reason10videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective8videos
SUPERPOSITION OF WAVES
Similar Questions
Four souces of sound each of sound level 10dB are sounded together in phase, the resultant intensity level will be (110/n) dB. Find value of n (log102=0.3).
View SolutionDay time sound level in silent zone is
View SolutionThe intensity level of two sounds are 100 dB and 50 dB. What is the ratio of their intensities?
View Solution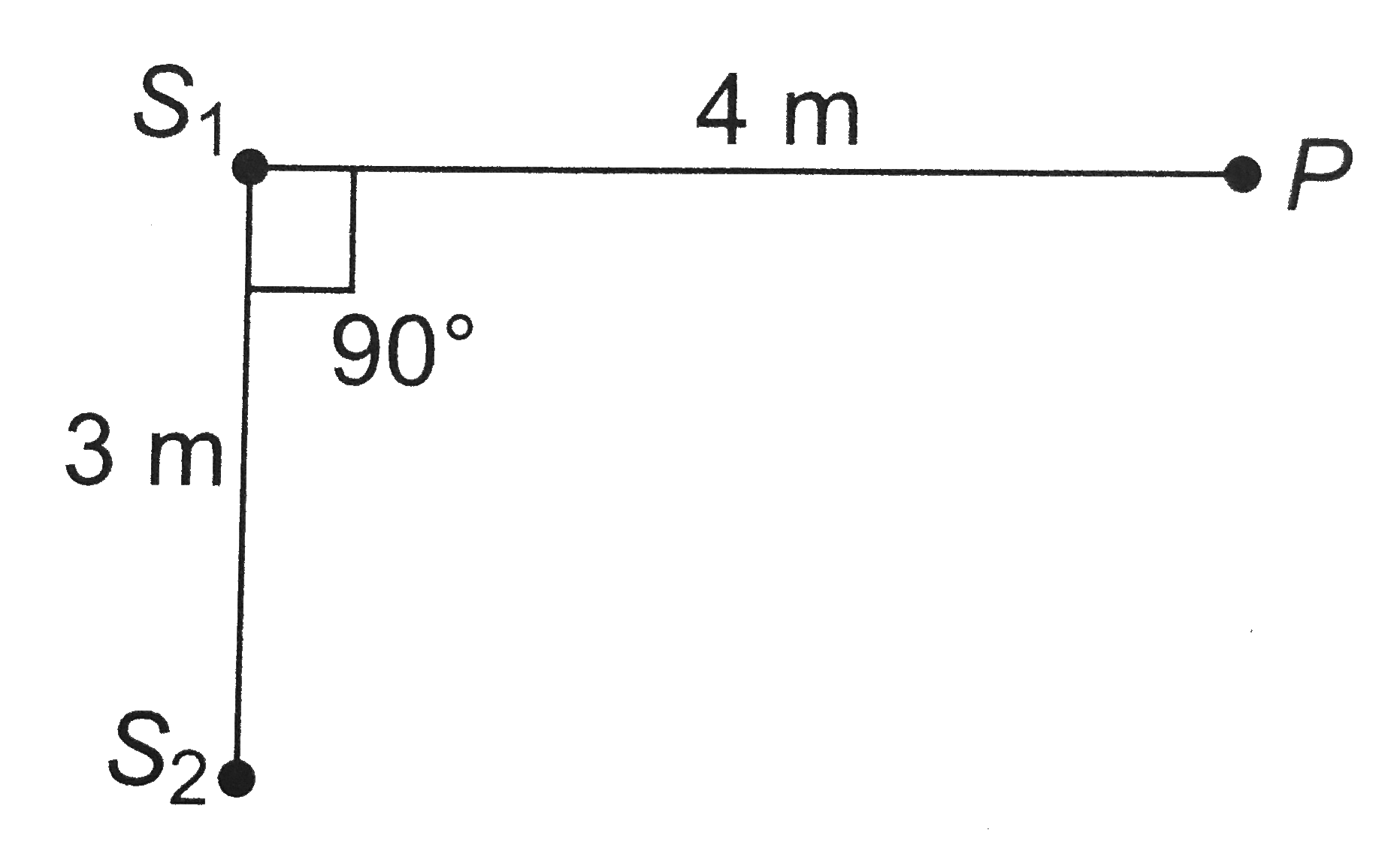
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P isView SolutionTwo sound sources of frequency 9Hz and 11Hz are sounded together then which plot is correct after superposition of sound waves.
View SolutionTwo sound sources of frequency 9Hz and 11Hz are sounded together then which plot is correct after superposition of sound waves.
View SolutionFind the sound level in decibel of a sound wave which has an intensity of 10−4Wm−2 if I0=10−12Wm−2.
View SolutionCalculate the sound level (in decibels) of a sound wave that has an intensity of 4.00μWm2.
View SolutionName the unit used for measuring the sound level.
View SolutionWhen a person wears a hearing aid, the sound intensity level increases by 30 dB. The sound intensity increases by
View Solution

