Four souces of sound each of sound level 10dB are sounded together in phase, the resultant intensity level will be (110/n) dB. Find value of n (log102=0.3).
The correct Answer is:5
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have four sound sources, each with a sound level of 10 dB. When they are sounded together in phase, we need to find the resultant intensity level in the form of 110n dB and determine the value of n.
Step 2: Convert Decibels to Intensity
The sound level in decibels (dB) is given by the formula:
L=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity (usually 10−12W/m2).
For each source:
10=10log10(II0)
Dividing both sides by 10:
1=log10(II0)
Taking the antilogarithm:
II0=10⟹I=10I0
Step 3: Calculate the Total Intensity
Since we have four sources, the total intensity when they are in phase is:
Itotal=4I=4×10I0=40I0
Step 4: Convert Total Intensity Back to Decibels
Now, we convert the total intensity back to decibels:
Ltotal=10log10(ItotalI0)=10log10(40I0I0)=10log10(40)
Step 5: Simplify log10(40)
We can express 40 as 23×5:
log10(40)=log10(23)+log10(5)=3log10(2)+log10(5)
Using the approximation log10(2)≈0.3 and log10(5)≈0.7 (since log10(10)=1):
log10(40)≈3(0.3)+0.7=0.9+0.7=1.6
Step 6: Calculate the Total Loudness
Now substituting back into the loudness equation:
Ltotal=10×1.6=16dB
Step 7: Find the Resultant Intensity Level
The total intensity level is:
Ltotal=10+16=26dB
Step 8: Set Up the Equation
According to the problem, we have:
110n=26
Multiplying both sides by n:
110=26n
Dividing both sides by 26:
n=11026≈4.23
Step 9: Final Calculation
Since n must be a whole number, we round it to the nearest integer, which gives n=5.
Final Answer
The value of n is 5.
---
We have four sound sources, each with a sound level of 10 dB. When they are sounded together in phase, we need to find the resultant intensity level in the form of 110n dB and determine the value of n.
The sound level in decibels (dB) is given by the formula:
L=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity (usually 10−12W/m2).
10=10log10(II0)
Dividing both sides by 10:
1=log10(II0)
Taking the antilogarithm:
II0=10⟹I=10I0
Since we have four sources, the total intensity when they are in phase is:
Itotal=4I=4×10I0=40I0
Now, we convert the total intensity back to decibels:
Ltotal=10log10(ItotalI0)=10log10(40I0I0)=10log10(40)
We can express 40 as 23×5:
log10(40)=log10(23)+log10(5)=3log10(2)+log10(5)
Using the approximation log10(2)≈0.3 and log10(5)≈0.7 (since log10(10)=1):
log10(40)≈3(0.3)+0.7=0.9+0.7=1.6
Now substituting back into the loudness equation:
Ltotal=10×1.6=16dB
The total intensity level is:
Ltotal=10+16=26dB
According to the problem, we have:
110n=26
Multiplying both sides by n:
110=26n
Dividing both sides by 26:
n=11026≈4.23
Since n must be a whole number, we round it to the nearest integer, which gives n=5.
The value of n is 5.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Four sources of sound each of sound level 10dB are sounded together in phase , the resultant intensity level will be (log102=0.3)
View SolutionWhen a person wears a hearing aid, the sound intensity level increases by 30 dB. The sound intensity increases by
View SolutionA person standing at distance r from a point source listen the sound emitted by the source. When person move to another point having distance r10 from the point source, then increase in sound intensity level is n×101 decibles value of n is ?
View SolutionThe intensity level of two sounds are 100 dB and 50 dB. What is the ratio of their intensities?
View SolutionCalculate the sound level (in decibels) of a sound wave that has an intensity of 4.00μWm2.
View SolutionAn increase in intensity level of 1 dB implies an increase in intensity of (given anti log100.1=1.2589)
View Solution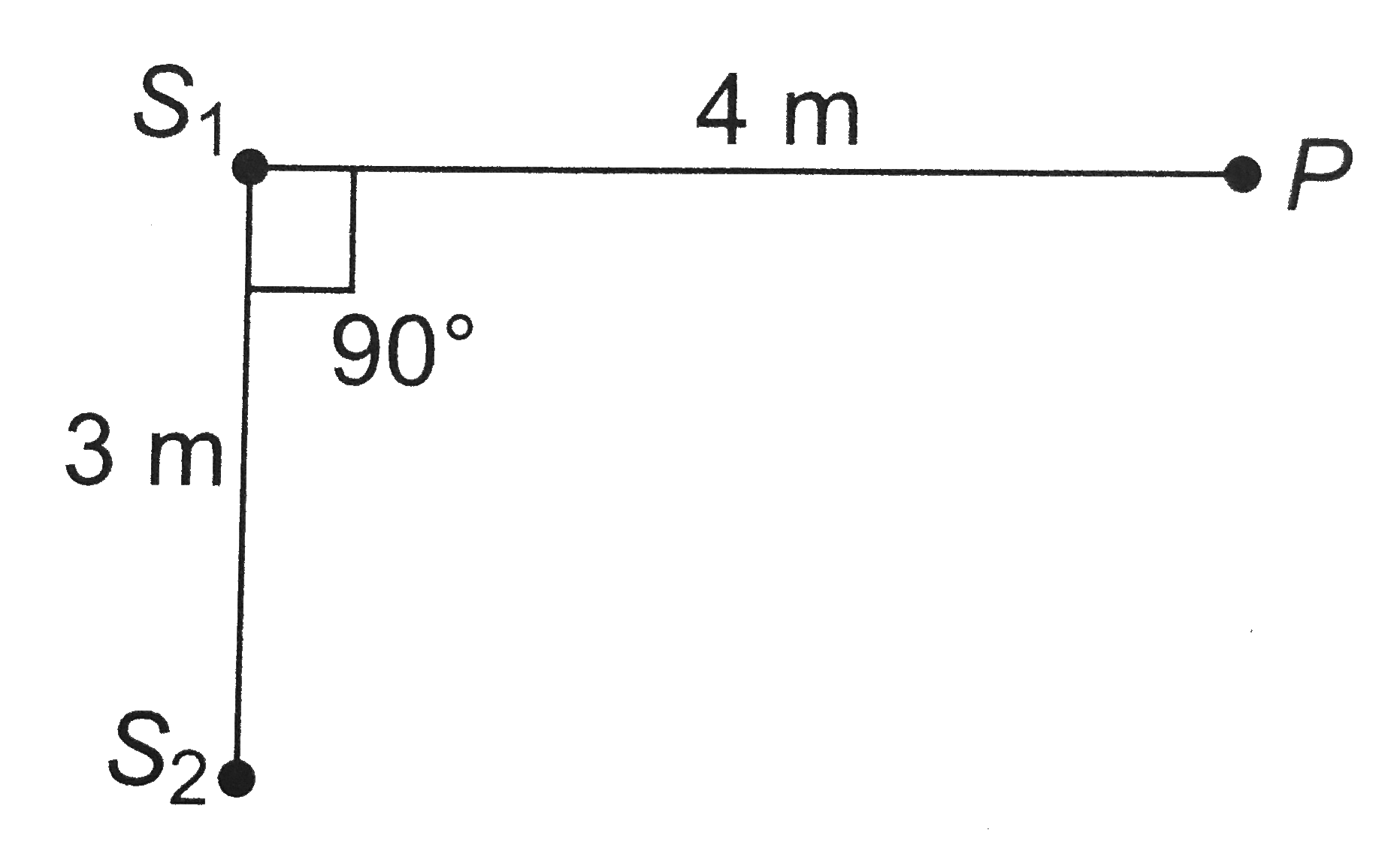
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionStatement I: A 80 dB sound has twice the intensity of a 40 dB sound.
Statement II: Loudness of a sound of a certain intensity I is defined as
L(in dB)=10log10(II0)
View SolutionThe sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be (a) 100 dB and (b) 10.0 dB?
View SolutionThe sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be (a) 100 dB and (b) 10.0 dB?
View Solution
