What are the maximum and minimum values of unknown resistance X, which can be determined using the post office box shown in the figure?
To determine the maximum and minimum values of the unknown resistance X using the post office box, we can follow these steps:
Step 1: Understand the Balancing Condition
The balancing condition for a Wheatstone bridge (post office box) is given by the formula:
PQ=RX
From this, we can rearrange the equation to find X:
X=Q⋅RP
Step 2: Identify the Maximum and Minimum Values
To find the maximum value of X, we need to maximize Q and R while minimizing P. Conversely, to find the minimum value of X, we need to minimize Q and R while maximizing P.
Step 3: Determine the Values of P, Q, and R
- For P:
- Maximum Pmax=1000+100+10=1110Ω
- Minimum Pmin=10Ω
- For Q:
- Maximum Qmax=10+100+1000=1110Ω
- Minimum Qmin=10Ω
- For R:
- Maximum Rmax=5000+2000+2000+500+200+200+100=9000Ω
- Minimum Rmin=100Ω
Step 4: Calculate the Maximum Value of X
Using the values for maximum Q and R and minimum P:
Xmax=Qmax⋅RmaxPmin=1110⋅900010
Calculating this gives:
Xmax=999000010=999000Ω=0.99MΩ
Step 5: Calculate the Minimum Value of X
Using the values for minimum Q and R and maximum P:
Xmin=Qmin⋅RminPmax=10⋅1001110
Calculating this gives:
Xmin=10001110≈0.900Ω
Final Results
- Maximum value of X: 0.99MΩ
- Minimum value of X: 0.9Ω
The balancing condition for a Wheatstone bridge (post office box) is given by the formula:
PQ=RX
From this, we can rearrange the equation to find X:
X=Q⋅RP
To find the maximum value of X, we need to maximize Q and R while minimizing P. Conversely, to find the minimum value of X, we need to minimize Q and R while maximizing P.
- For P:
- Maximum Pmax=1000+100+10=1110Ω
- Minimum Pmin=10Ω
- Maximum Qmax=10+100+1000=1110Ω
- Minimum Qmin=10Ω
- Maximum Rmax=5000+2000+2000+500+200+200+100=9000Ω
- Minimum Rmin=100Ω
Using the values for maximum Q and R and minimum P:
Xmax=Qmax⋅RmaxPmin=1110⋅900010
Calculating this gives:
Xmax=999000010=999000Ω=0.99MΩ
Using the values for minimum Q and R and maximum P:
Xmin=Qmin⋅RminPmax=10⋅1001110
Calculating this gives:
Xmin=10001110≈0.900Ω
- Maximum value of X: 0.99MΩ
- Minimum value of X: 0.9Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Example Type 1
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Example Type 2
Explore 1 Video
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
In the figure shown below, the maximum and the minimum possible unknown resistance (X), that can be measured by the post office box are Xmax and Xmin respectively. Then the ratio of these two resistances is : (In this experiment we take out only one plug in arm AB and only one plug in arm BC, but in arm AD we can take out any no. of plugs) :
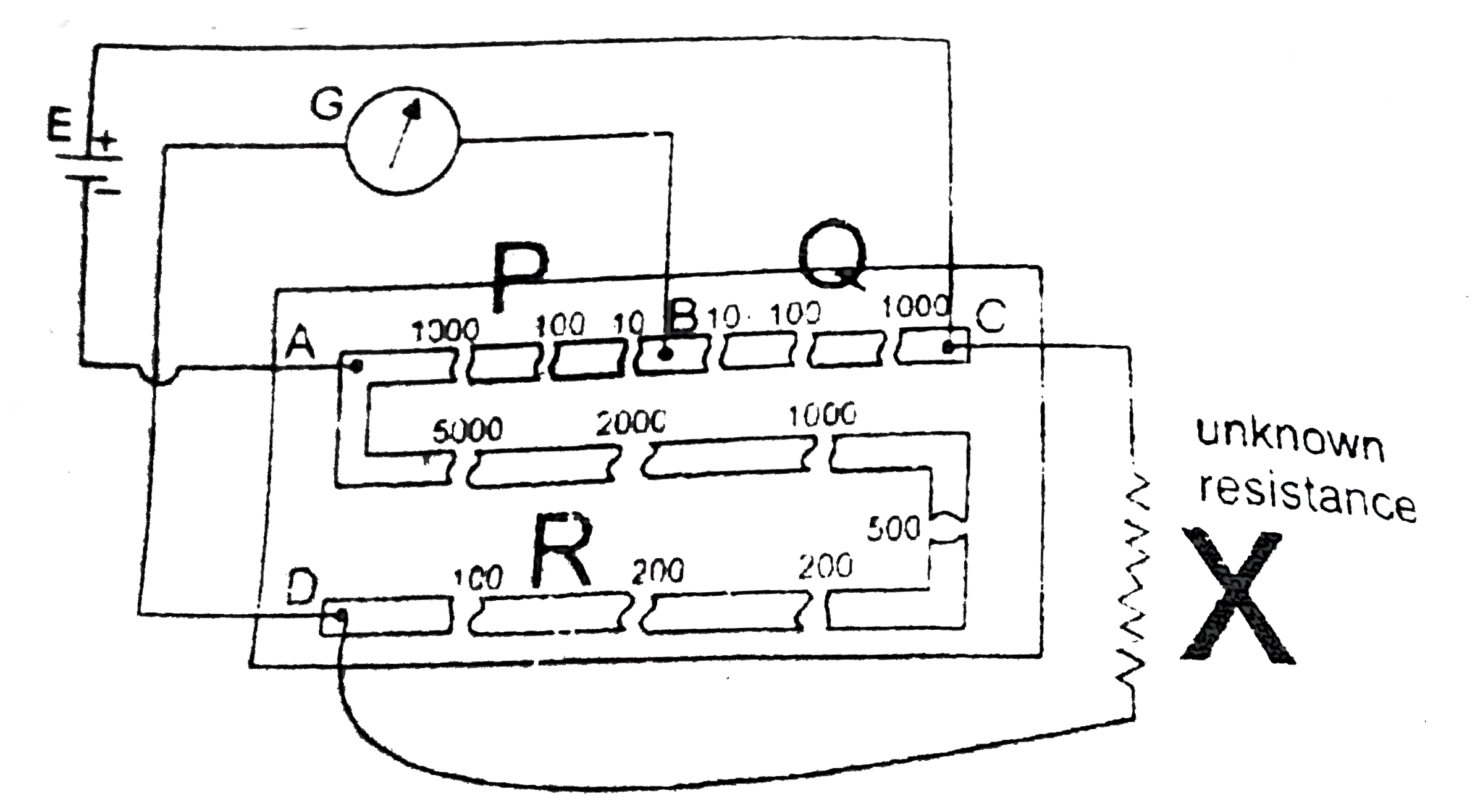
View SolutionFor what value of unknown resistance X, the potential difference between B and D will be zero in the circuit shown in the figure ?
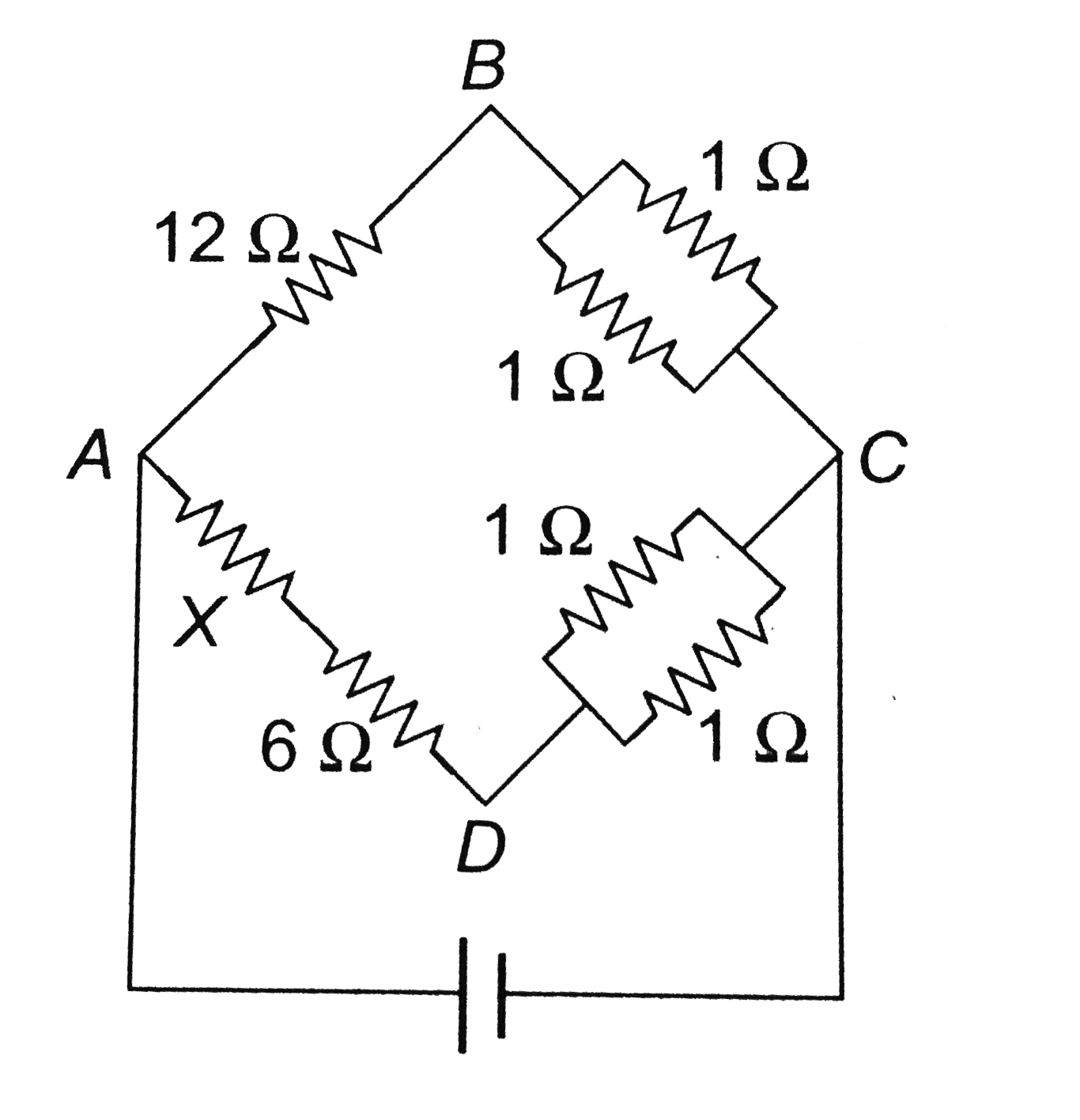
View SolutionFind the maximum and minimum values of f(x)=2x3+5 on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=x3−1 on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=|x+2| on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=sin2x+5 on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=|sin4x+3| on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=−|x+1|+3 on R , if any, without using derivatives.
View SolutionFind the maximum and minimum values of f(x)=−(x−1)2+2 on R , if any, without using derivatives.
View SolutionIn Figure, determine the value of x
View Solution
