For a cell, the terminal potential difference is 2.2V, when circuit is open and reduces to 1.8V. When cell is connected to a resistance R=5Ω, the internal resistance of cell (R) is
109Ω
910Ω
119Ω
59Ω
The correct Answer is:A
To find the internal resistance of the cell, we can follow these steps:
Step 1: Identify the given values
- Terminal potential difference when the circuit is open (E) = 2.2 V
- Terminal potential difference when the circuit is closed (V) = 1.8 V
- External resistance (R) = 5 Ω
Step 2: Understand the relationship between EMF, terminal voltage, and internal resistance
When the circuit is closed, the terminal voltage (V) is given by the formula:
V=E−I⋅r
Where:
- E is the EMF of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
Step 3: Calculate the current (I) when the circuit is closed
Using Ohm's law, the current I can be calculated as:
I=ER+r
Substituting E=2.2V and R=5Ω:
I=2.25+r
Step 4: Substitute the current into the terminal voltage equation
We know that when the circuit is closed, the terminal voltage is 1.8 V:
1.8=2.2−I⋅r
Substituting I from Step 3:
1.8=2.2−(2.25+r)⋅r
Step 5: Rearranging the equation
Rearranging gives:
1.8=2.2−2.2r5+r
2.2−1.8=2.2r5+r
0.4=2.2r5+r
Step 6: Cross-multiply to eliminate the fraction
Cross-multiplying gives:
0.4(5+r)=2.2r
2+0.4r=2.2r
Step 7: Solve for r
Rearranging the equation:
2=2.2r−0.4r
2=1.8r
r=21.8=2018=109Ω
Final Result
The internal resistance of the cell r is:
r=109Ω
---
- Terminal potential difference when the circuit is open (E) = 2.2 V
- Terminal potential difference when the circuit is closed (V) = 1.8 V
- External resistance (R) = 5 Ω
When the circuit is closed, the terminal voltage (V) is given by the formula:
V=E−I⋅r
Where:
- E is the EMF of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
Using Ohm's law, the current I can be calculated as:
I=ER+r
Substituting E=2.2V and R=5Ω:
I=2.25+r
We know that when the circuit is closed, the terminal voltage is 1.8 V:
1.8=2.2−I⋅r
Substituting I from Step 3:
1.8=2.2−(2.25+r)⋅r
Rearranging gives:
1.8=2.2−2.2r5+r
2.2−1.8=2.2r5+r
0.4=2.2r5+r
Cross-multiplying gives:
0.4(5+r)=2.2r
2+0.4r=2.2r
Rearranging the equation:
2=2.2r−0.4r
2=1.8r
r=21.8=2018=109Ω
The internal resistance of the cell r is:
r=109Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Subjective
53 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Assertion And Reason
11 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The poten tial difference between the terminals of a cells is found to be 3 volts when it is connected to a resistance equal to its internal resistance. The e.m.f. of the cell is:-
View SolutionWhen current supplied by a cell to a circuit is 0.3A, its terminal potential difference is 0.9 A. When the current supplied becomes 0.2 A, its terminal potential difference becomes 1.0 V . The internal resistance of the cell is
View SolutionThe terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionA standerd cell emf 1.08Vis balance by the potential difference across 91cm of a meter long wire applied by a cell of emf 2V through a series resistor of resistance 2Ω. The internal resistance of the cell is zero. Find the resistance per unit length of the potentiometer wire.
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
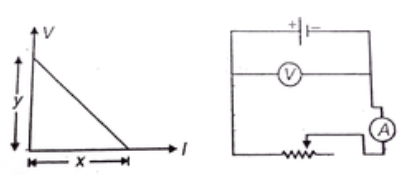
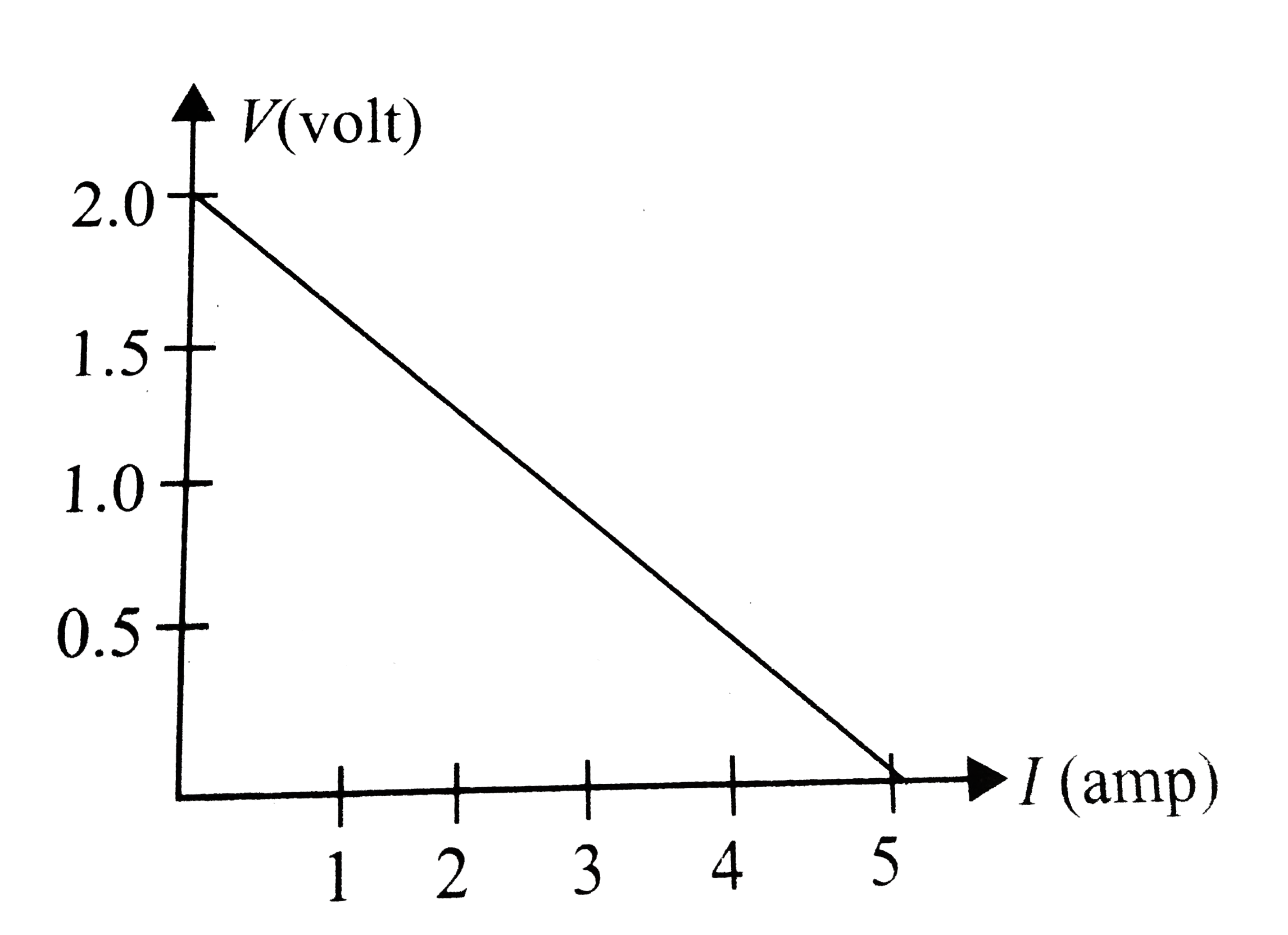
View SolutionFor a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn the cell. The emf and the internal resistance of the cell are E and r, respectively. Then
View SolutionWhen a Daniel cell is connected in the secondary circuit of a potentiometer, the balancing length is found to be 540 cm. If the balancing length becomes 500 cm. When the cell is short-circuited with 1Ω, the internal resistance of the cell is
View Solution
