A 2μF capacitor C1 is charge to a voltage 100 V and a 4μF capacitor C2 is charged to a voltage 50 V. The capacitors are then connected in parallel What is the loss of energy due to parallel connection?
1.7J
0.17J
1.7×10−2J
1.7×10−3J
The correct Answer is:D
To solve the problem, we need to determine the energy loss when two capacitors are connected in parallel. Here’s a step-by-step solution:
Step 1: Calculate the initial energy stored in each capacitor
The energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage.
For capacitor C1 (2 µF charged to 100 V):
U1=12×2×10−6F×(100V)2=12×2×10−6×10000=10×10−3J=0.01J
For capacitor C2 (4 µF charged to 50 V):
U2=12×4×10−6F×(50V)2=12×4×10−6×2500=5×10−3J=0.005J
Step 2: Calculate the total initial energy
The total initial energy Uinitial is the sum of the energies stored in both capacitors:
Uinitial=U1+U2=0.01J+0.005J=0.015J
Step 3: Calculate the total charge and equivalent capacitance when connected in parallel
The total charge Q when the capacitors are connected in parallel is the sum of the individual charges:
Q1=C1×V1=2×10−6×100=200×10−6C=200μC
Q2=C2×V2=4×10−6×50=200×10−6C=200μC
Qtotal=Q1+Q2=200μC+200μC=400μC
The equivalent capacitance Ceq when connected in parallel is:
Ceq=C1+C2=2μF+4μF=6μF
Step 4: Calculate the final voltage across the capacitors
The final voltage Vf across the capacitors when connected in parallel is given by:
Vf=QtotalCeq=400×10−66×10−6=4006≈66.67V
Step 5: Calculate the final energy stored in the equivalent capacitor
The final energy Ufinal stored in the equivalent capacitor is:
Ufinal=12CeqV2f=12×6×10−6×(66.67)2
Calculating (66.67)2:
(66.67)2≈4444.44
Thus,
Ufinal=12×6×10−6×4444.44≈13.33×10−3J=0.01333J
Step 6: Calculate the energy loss
The energy loss ΔU due to the parallel connection is:
ΔU=Uinitial−Ufinal=0.015J−0.01333J≈0.00167J
Final Answer
The loss of energy due to the parallel connection is approximately:
ΔU≈1.67mJ
U=12CV2
where C is the capacitance and V is the voltage.
U1=12×2×10−6F×(100V)2=12×2×10−6×10000=10×10−3J=0.01J
U2=12×4×10−6F×(50V)2=12×4×10−6×2500=5×10−3J=0.005J
Uinitial=U1+U2=0.01J+0.005J=0.015J
Q1=C1×V1=2×10−6×100=200×10−6C=200μC
Q2=C2×V2=4×10−6×50=200×10−6C=200μC
Qtotal=Q1+Q2=200μC+200μC=400μC
Ceq=C1+C2=2μF+4μF=6μF
Vf=QtotalCeq=400×10−66×10−6=4006≈66.67V
Ufinal=12CeqV2f=12×6×10−6×(66.67)2
Calculating (66.67)2:
(66.67)2≈4444.44
Thus,
Ufinal=12×6×10−6×4444.44≈13.33×10−3J=0.01333J
ΔU=Uinitial−Ufinal=0.015J−0.01333J≈0.00167J
The loss of energy due to the parallel connection is approximately:
ΔU≈1.67mJ
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
C1=5.6μF is charged upto 220V. Another capacitor C2=2.8μF is connected in parallel. Find loss in energy ?
View SolutionA capacitor of 0.75μF is charged to a voltage of 16 V. What is the magnitude of the charge on each plate of the capacitor ?
View SolutionFind the charges on 6μF and 4μF capacitors
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate the capacity of second capacitor.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View Solution4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
View Solution4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
View SolutionA 2μF capacitor is charged to 100V, and then its plates are connected by a conducting Wire. The heat produced is .
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionA 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
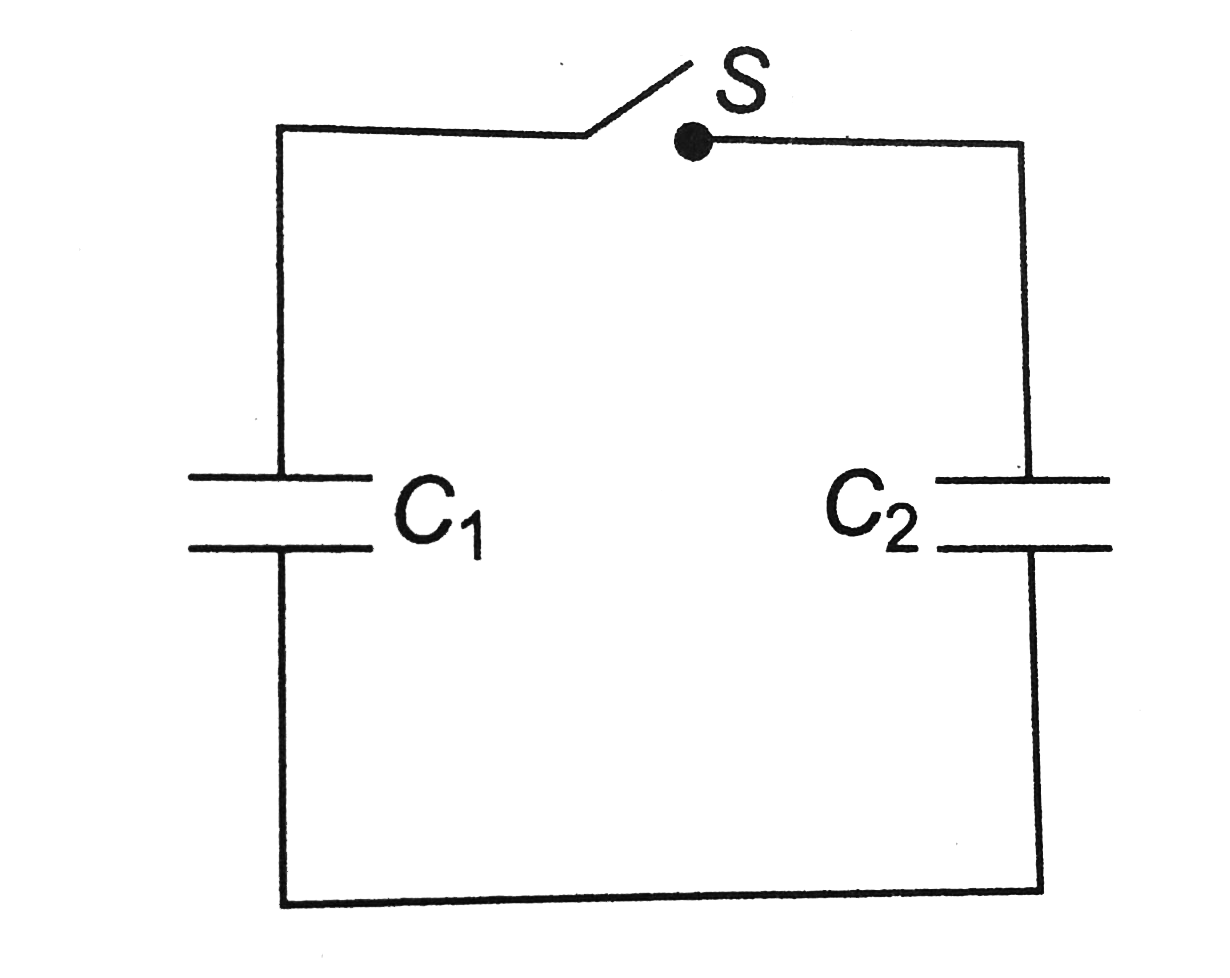
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View Solution
