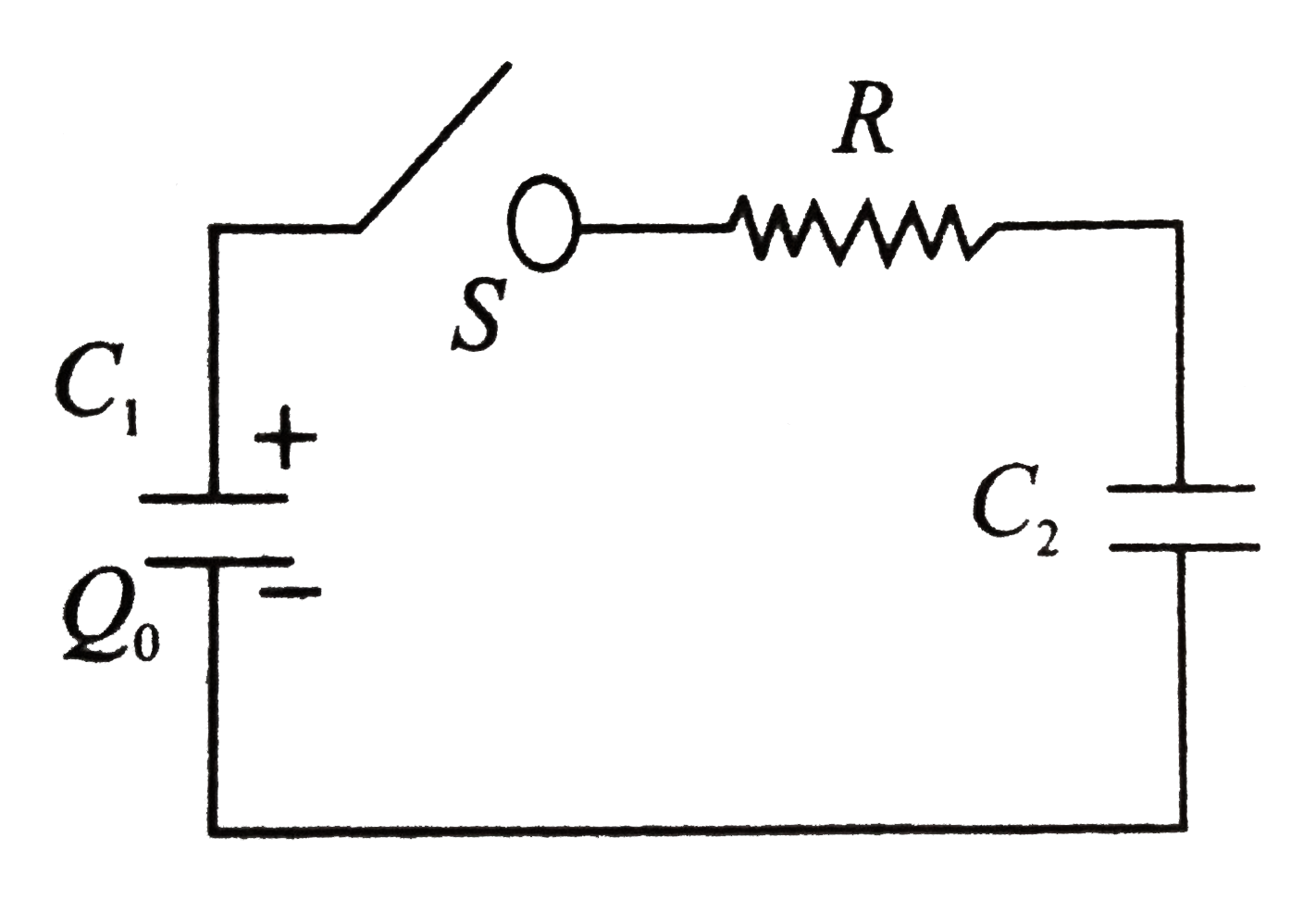
The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed,capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
find the charge flown through wires as a function of time is
where C=C1C2C1+C2
q0e−tRC+CC2q0
q0CC1x[1−e−tRC]
q0CC1e−tCR
q0e−tRC
The correct Answer is:B
Finally the capacitors are in parallel and total charge (=q0) distributes between them in direct ratio of capacity.
∴qC2=(C2C1+C2)q0→ in steady state .
but this chasrge increases exponentially.
Hence, charge on C2 at any time t is
qC2=(C2q0C1+C2)(1−e−tτC)
Initially C2 is uncharged so, what ever is the charge on C2 it is charge flown through switches.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
The capacitor C1 in the flgure shown initially carries a charge q0. When the switches S1 and S2 are closed,capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
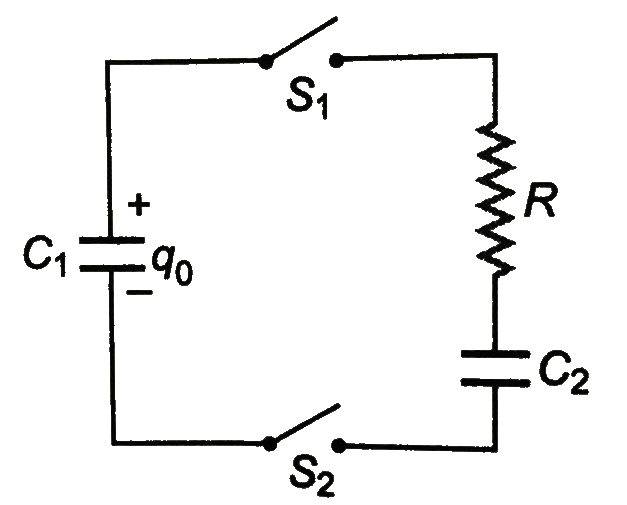
the total heat dissipated in the circuit during the discharging process of C1 isView SolutionThe capacitor C1 in the figure initially carries a charge q0. When the switch S1 and S2 are shut, capacitor C1 is connected in series to a resistor R and a second capacitor C2, which initially does not carry any charge.
If the heat lost in the resistor after a long time of closing the switch is q20C2kC1(C1+C2), then Find the value of k.
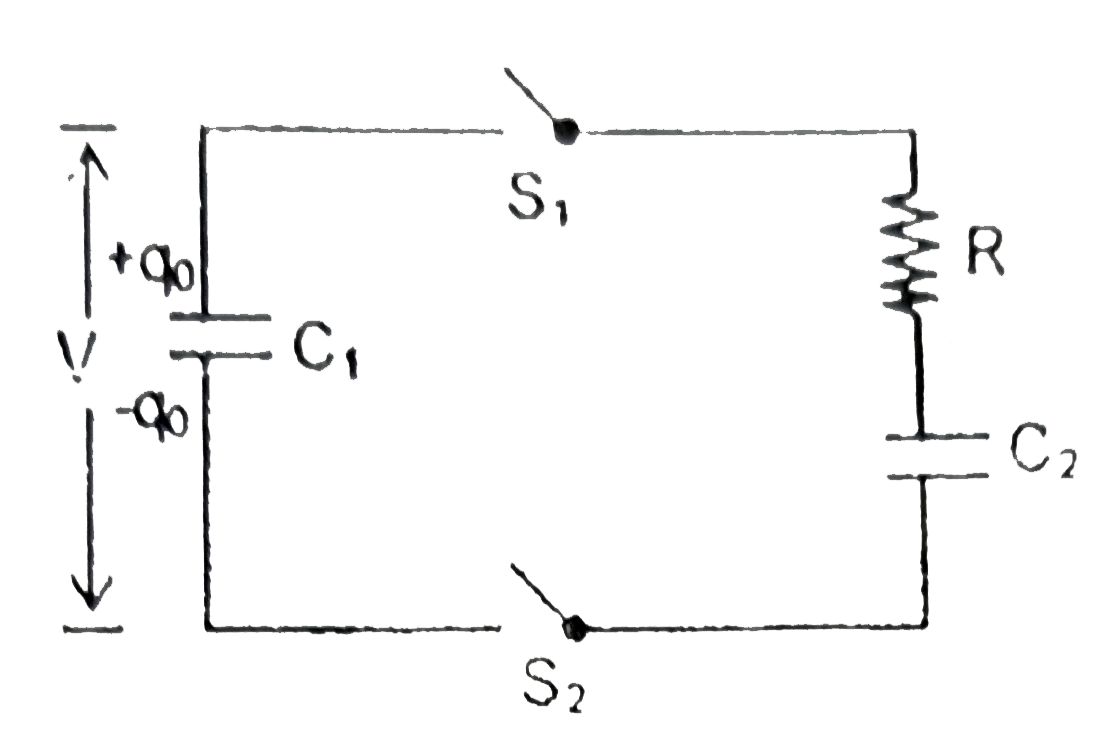View SolutionThe capactor C1 in the figure initially carries a charge q0. When the i switch S1 and S2 are closed, capacitor C1 is connected to a resistor R and a second capacitor C2, which initially does not carry any charge.
(a) Find the charges deposited on the capacitors in steady state and the current through R as a function of time.
(b) What is heat lost in the resistor after a long time of closing the switch?
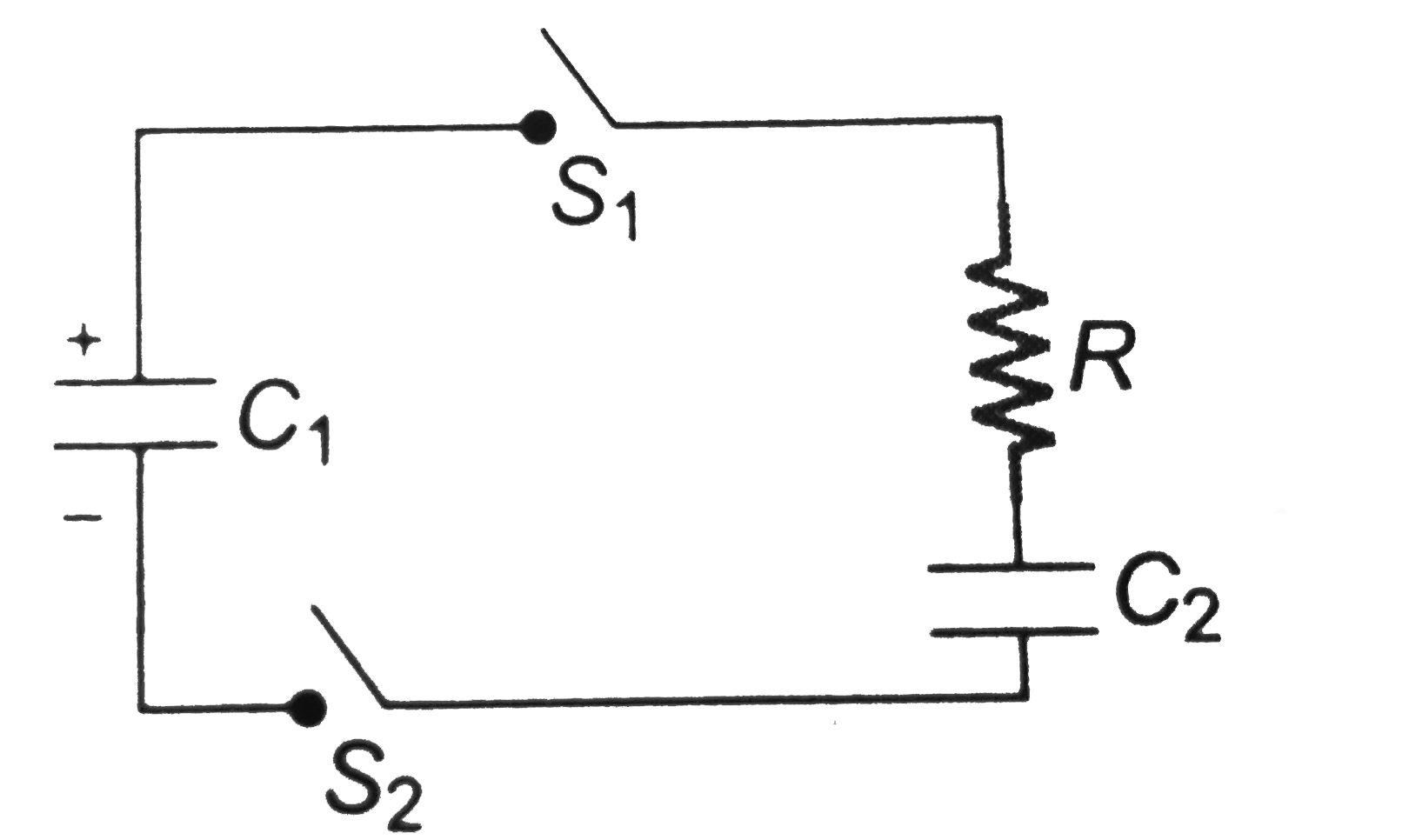View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.
View SolutionIn the circuit shown initially C1,C2 are uncharged. After closing the switch
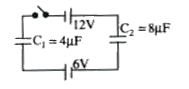View SolutionIn the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionThree capacitors are connected as shwn in. Then, the charge on capacitor C1 is .
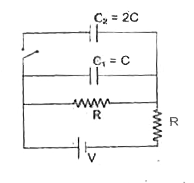
. View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
Energy in C1 isView SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View Solution