Assertion At some given instant I1 and I2 both are 2A each. Then, I at this should be zero.
Reason : There is a phase difference of I1 and I2functions.
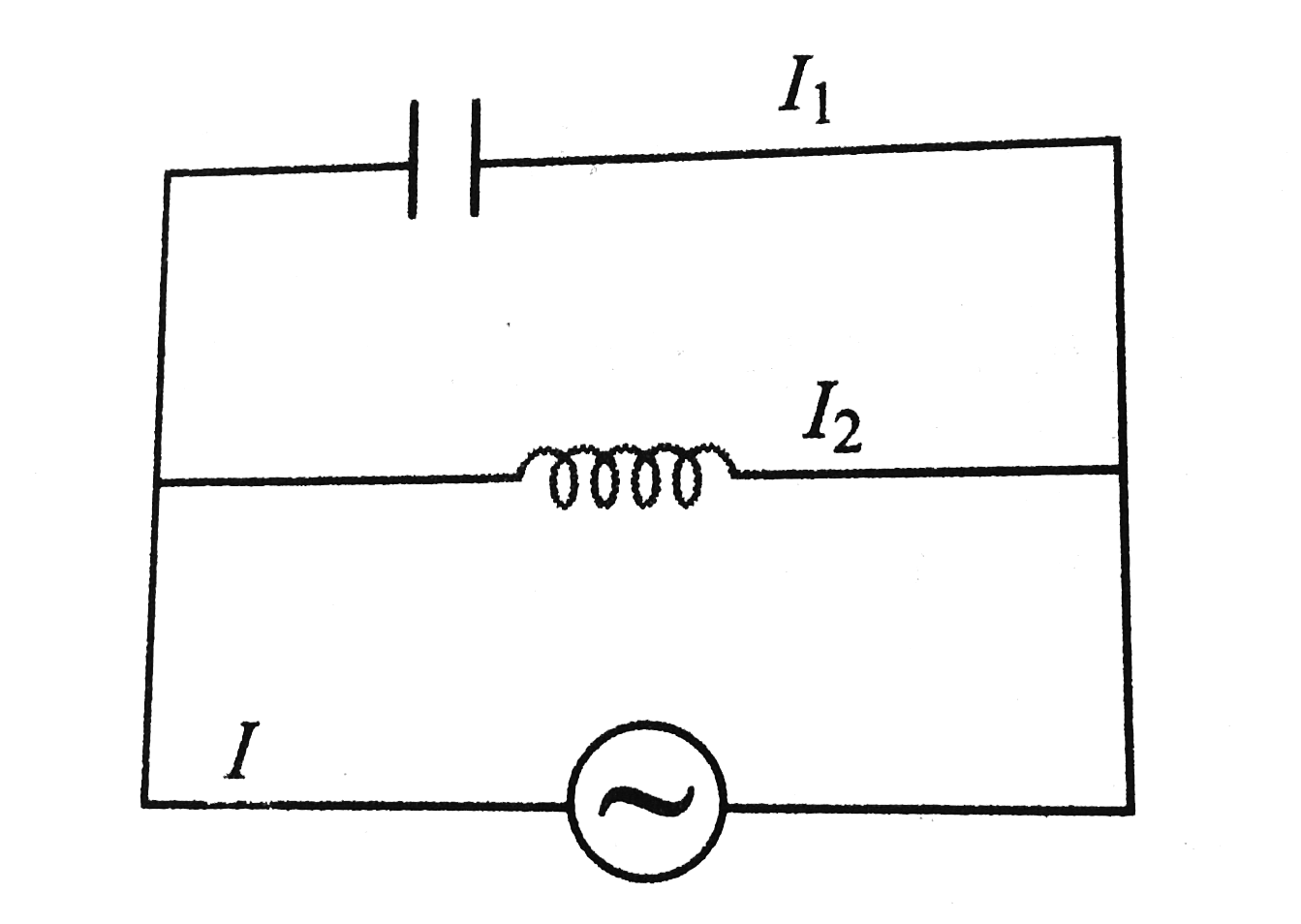
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
NA
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Objective30videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 28.22videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
In the shown AC circuit phase different between current I1 and I2 is
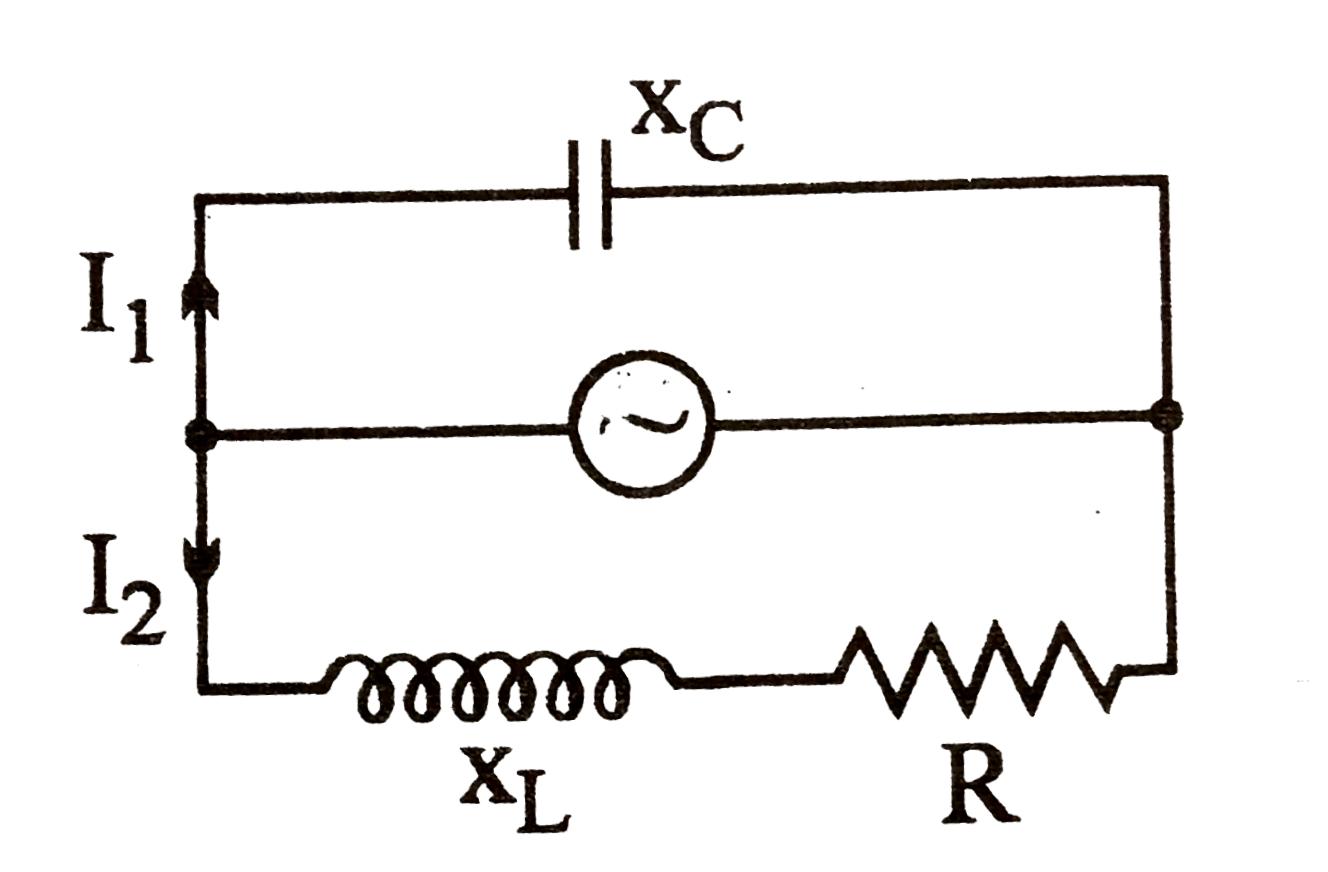View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
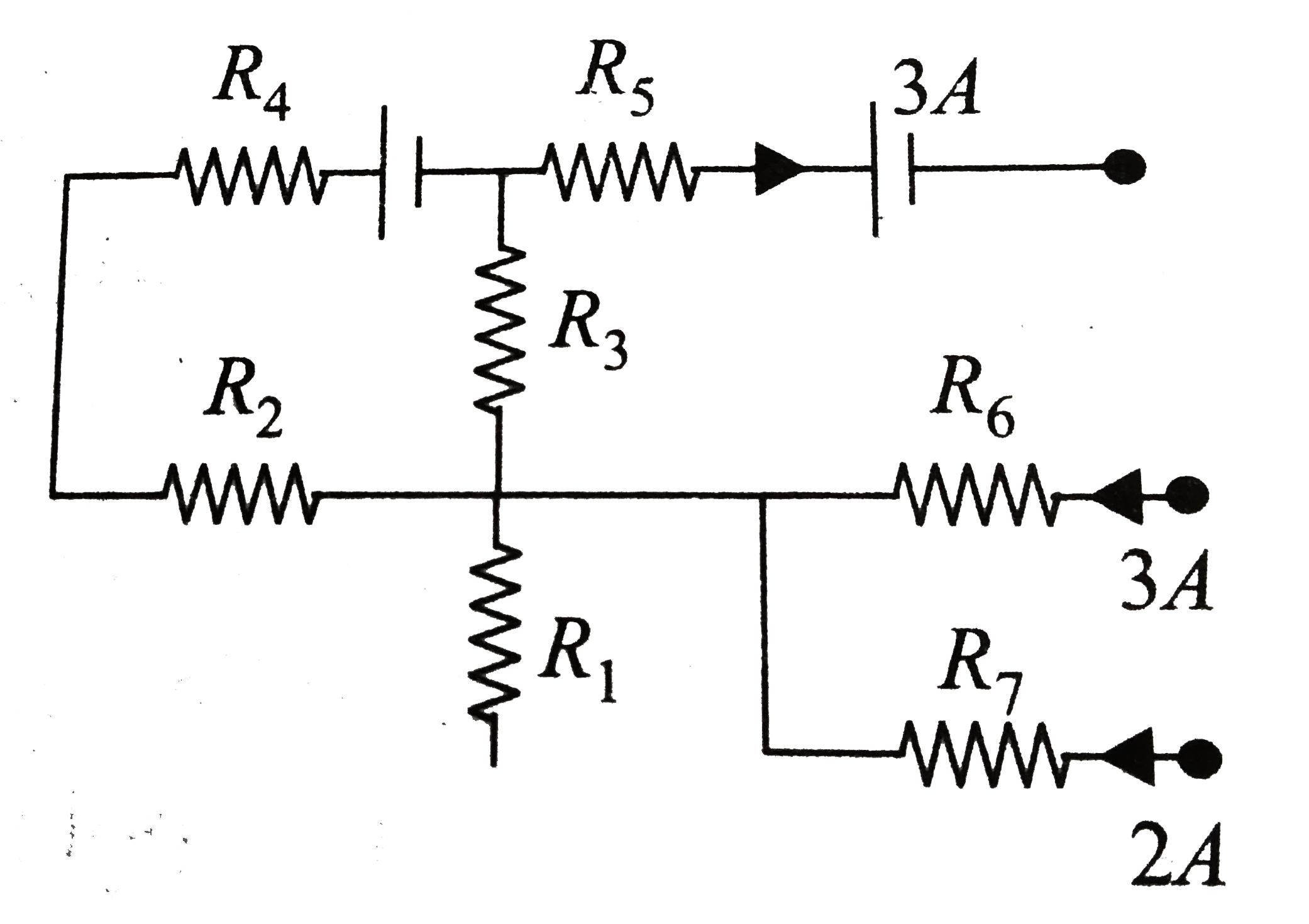. View SolutionCurrent I1andI2 flow in the wires shown in Fig. The field is zero at distance x to the right of O. Then
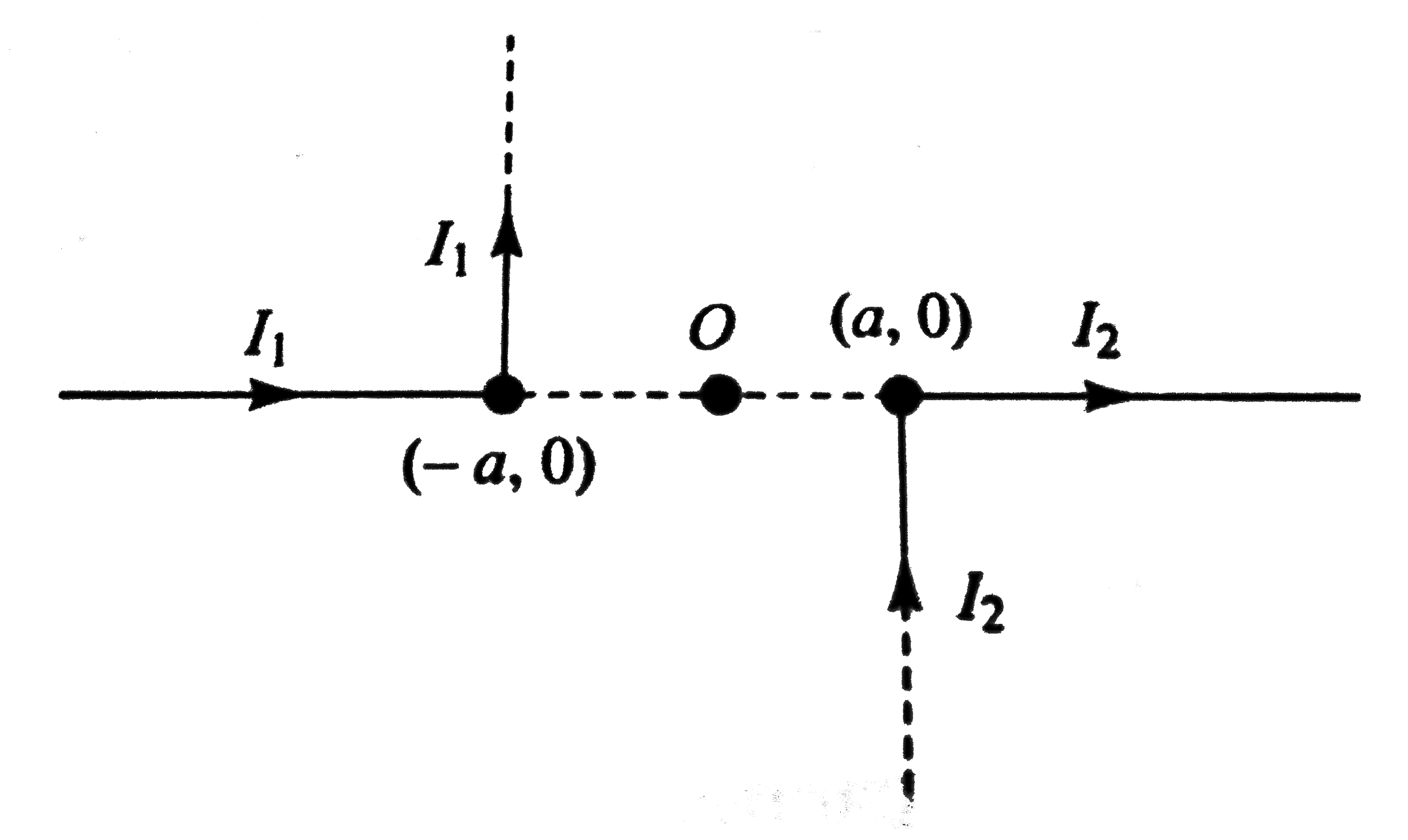View Solution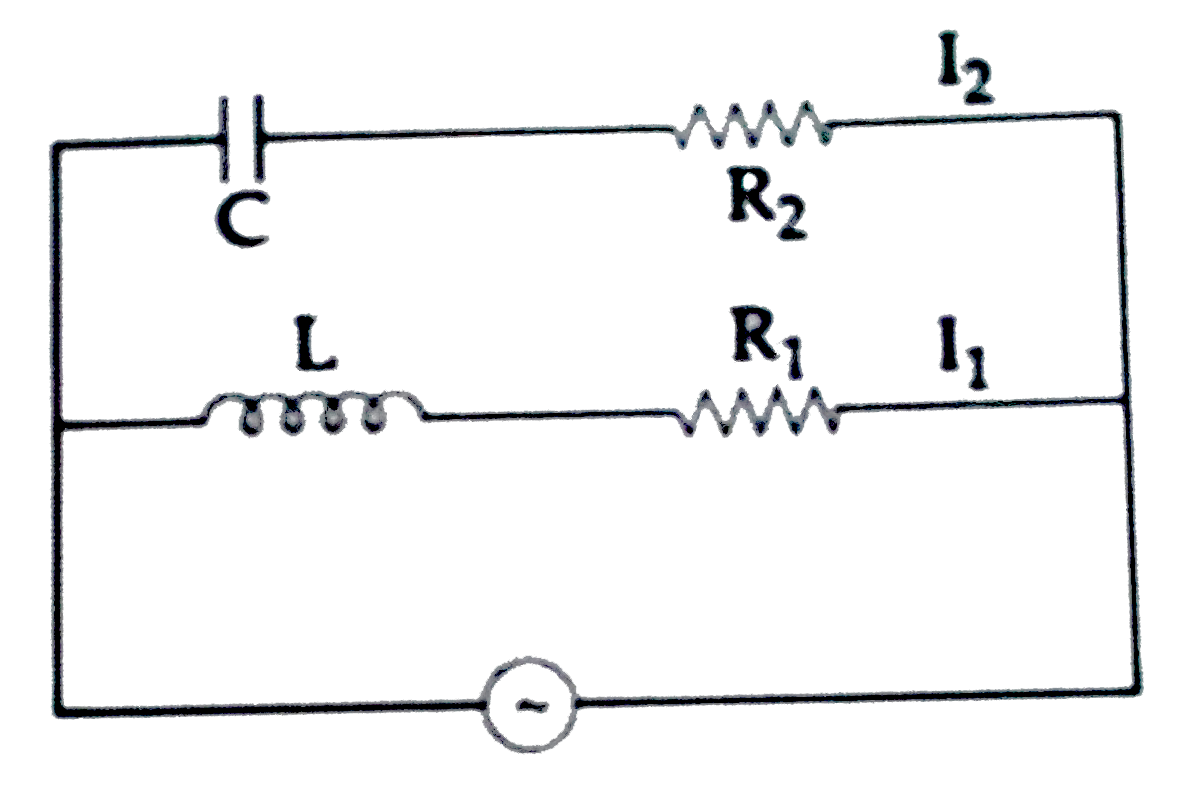
In the value circuit, C=√32μF,R2=20Ω,L=√310H, and R1=10Ω .Current in L−R1 path is I1 and in C−R2 path it is I2. The voltage of A.C source is given by, V=200√2sin(100t) volts. The phase difference between I2 and I1 is :View SolutionFind the phase difference between i1andi2 in the two branches of the circuit shown.
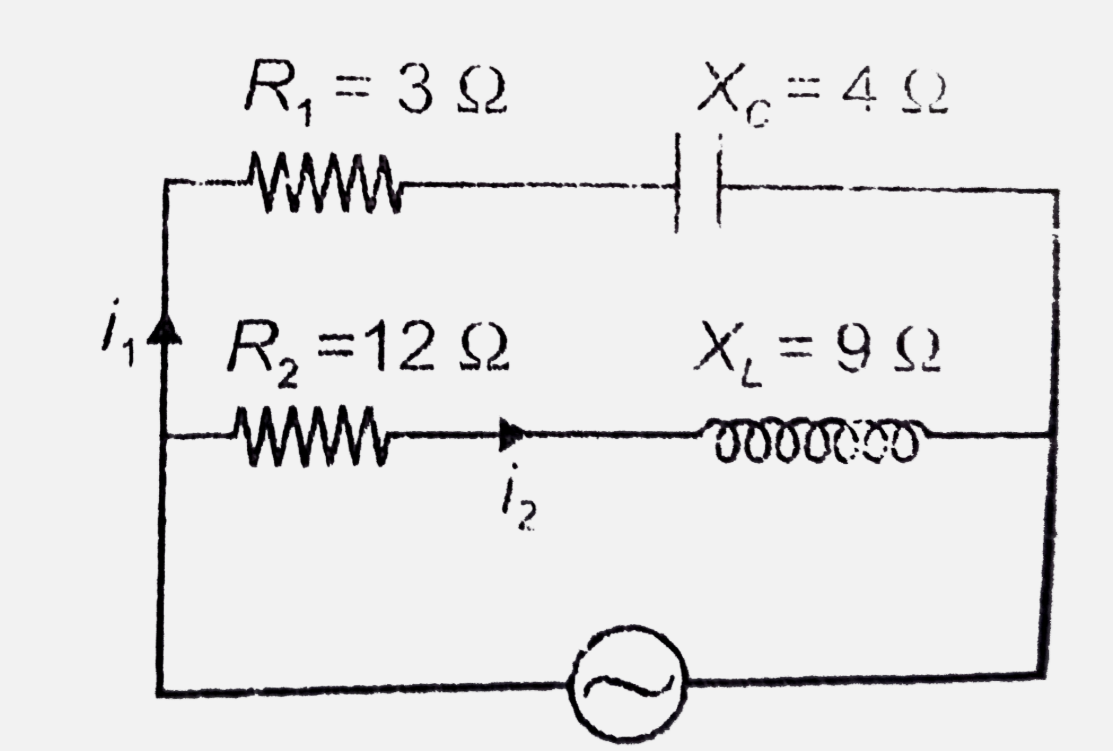View SolutionIn the following circuit i1 and i2are respectively
View SolutionAssertion :- There are six different combinations or genotypes
of the human ABO blood types.
Reason :- The gene (I) has three alleles IA,IBandI0View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given byView SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given byView SolutionConsider an interference pattern between two coherent sources. If I1andI2 be intensities at points where the phase difference are π3and2π3 and respectively , then the intensity at maxima is
View Solution