A glass sphere with 10cm radius has a 5cm radius spherical hole at its centre. A narraow beam of parallel light is directed into the sphere. Where, if anywhere, will the sphere produce an image? The index of refraction of the glass is 1.50.
The correct Answer is:A, C, D
To solve the problem step by step, we will analyze the refraction of light through the glass sphere with a central spherical hole. The goal is to determine where the images are formed as the light passes through the sphere.
Step 1: Understand the Geometry of the Problem
We have a glass sphere with a radius of 10 cm and a central spherical hole with a radius of 5 cm. The refractive index of glass is given as n2=1.5 and the refractive index of air is n1=1.
Step 2: Identify the Surfaces
The sphere has four surfaces where refraction occurs:
1. Surface 1 (outer surface of the sphere)
2. Surface 2 (inner surface of the hole)
3. Surface 3 (inner surface of the sphere)
4. Surface 4 (outer surface of the hole)
Step 3: Refraction at Surface 1
Using the formula for refraction at a spherical surface:
n2V−n1U=n2−n1R
Here, U=−∞ (object at infinity), R=10 cm (radius of the sphere), n2=1.5, and n1=1.
Substituting the values:
1.5V−1−∞=1.5−110
This simplifies to:
1.5V=0.510
V=1.5×100.5=30 cm
This means the first image I1 is formed 30 cm from the surface 1 in the direction of the incident light.
Step 4: Refraction at Surface 2
The image I1 acts as an object for surface 2. The distance from I1 to surface 2 is 30−5=25 cm (positive since it is in the direction of the incident light).
Using the same refraction formula:
U=25 cm,R=−5 cm,n2=1,n1=1.5
Substituting:
1V2−1.525=1−1.5−5
This simplifies to:
1V2=1.525−0.55
Calculating:
1V2=1.525−2.525=−125
Thus:
V2=−25 cm
This means the second image I2 is formed 25 cm to the left of surface 2.
Step 5: Refraction at Surface 3
The distance from I2 to surface 3 is 25+10=35 cm (negative since it is in the opposite direction).
Using the refraction formula:
U=−35 cm,R=−5 cm,n2=1.5,n1=1
Substituting:
1.5V3−1−35=1−1.5−5
This simplifies to:
1.5V3+135=−0.5−5
Calculating:
1.5V3+135=0.1
Solving for V3:
1.5V3=0.1−135
Calculating:
1.5V3=3.5−135=2.535
Thus:
V3=1.5×352.5=21 cm
Step 6: Refraction at Surface 4
The distance from I3 to surface 4 is 21+5=26 cm (negative since it is in the opposite direction).
Using the refraction formula:
U=−26 cm,R=−10 cm,n2=1,n1=1.5
Substituting:
1V4−1.5−26=1−1.5−10
This simplifies to:
1V4+1.526=−0.5−10
Calculating:
1V4+1.526=0.05
Solving for V4:
1V4=0.05−1.526
Calculating:
1V4=1.3−1.526=−0.226
Thus:
V4=−130 cm
Conclusion
The sphere produces four images at the following distances:
1. I1 at +30 cm
2. I2 at −25 cm
3. I3 at −21 cm
4. I4 at −130 cm
We have a glass sphere with a radius of 10 cm and a central spherical hole with a radius of 5 cm. The refractive index of glass is given as n2=1.5 and the refractive index of air is n1=1.
The sphere has four surfaces where refraction occurs:
1. Surface 1 (outer surface of the sphere)
2. Surface 2 (inner surface of the hole)
3. Surface 3 (inner surface of the sphere)
4. Surface 4 (outer surface of the hole)
Using the formula for refraction at a spherical surface:
n2V−n1U=n2−n1R
Here, U=−∞ (object at infinity), R=10 cm (radius of the sphere), n2=1.5, and n1=1.
1.5V−1−∞=1.5−110
This simplifies to:
1.5V=0.510
V=1.5×100.5=30 cm
This means the first image I1 is formed 30 cm from the surface 1 in the direction of the incident light.
The image I1 acts as an object for surface 2. The distance from I1 to surface 2 is 30−5=25 cm (positive since it is in the direction of the incident light).
U=25 cm,R=−5 cm,n2=1,n1=1.5
Substituting:
1V2−1.525=1−1.5−5
This simplifies to:
1V2=1.525−0.55
Calculating:
1V2=1.525−2.525=−125
Thus:
V2=−25 cm
This means the second image I2 is formed 25 cm to the left of surface 2.
The distance from I2 to surface 3 is 25+10=35 cm (negative since it is in the opposite direction).
U=−35 cm,R=−5 cm,n2=1.5,n1=1
Substituting:
1.5V3−1−35=1−1.5−5
This simplifies to:
1.5V3+135=−0.5−5
Calculating:
1.5V3+135=0.1
Solving for V3:
1.5V3=0.1−135
Calculating:
1.5V3=3.5−135=2.535
Thus:
V3=1.5×352.5=21 cm
The distance from I3 to surface 4 is 21+5=26 cm (negative since it is in the opposite direction).
U=−26 cm,R=−10 cm,n2=1,n1=1.5
Substituting:
1V4−1.5−26=1−1.5−10
This simplifies to:
1V4+1.526=−0.5−10
Calculating:
1V4+1.526=0.05
Solving for V4:
1V4=0.05−1.526
Calculating:
1V4=1.3−1.526=−0.226
Thus:
V4=−130 cm
The sphere produces four images at the following distances:
1. I1 at +30 cm
2. I2 at −25 cm
3. I3 at −21 cm
4. I4 at −130 cm
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions8videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct41videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.
 View Solution
View SolutionA glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre.The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surfaceView SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?
 View Solution
View SolutionA parallel beam of light falls on a solid tranparent sphere.
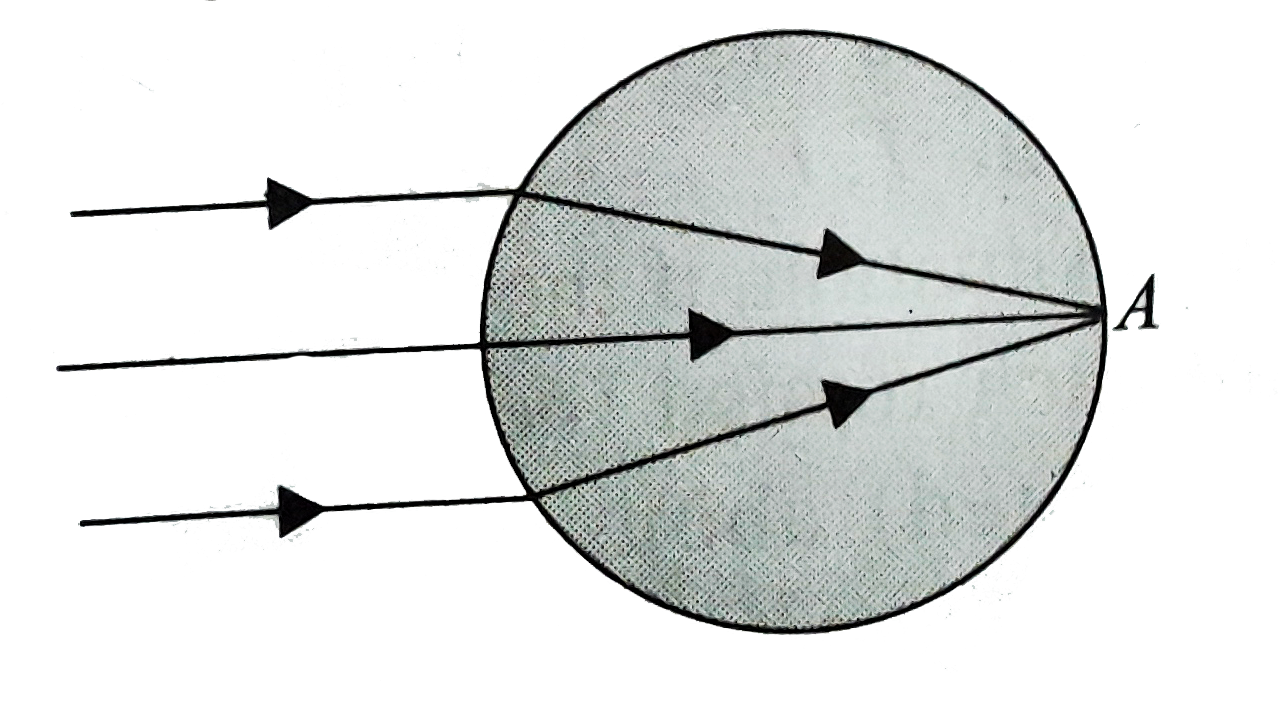
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,View SolutionThe radius of a sphere is 1.23 cm. What is its surface area?
View SolutionA glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is
 View Solution
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is
 View Solution
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is
 View Solution
View Solution

