White light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
The correct Answer is:A, C
To solve the problem regarding the missing wavelengths in the Young's double slit experiment with white light, we will follow these steps:
Step 1: Understand the Setup
We have two slits separated by a distance b and a screen located at a distance d from the slits. The point of interest on the screen is directly in front of one of the slits.
Step 2: Identify the Condition for Missing Wavelengths
At the point directly in front of one of the slits, certain wavelengths are missing due to destructive interference. For destructive interference to occur, the path difference between the light waves from the two slits must be an odd multiple of half the wavelength.
Step 3: Calculate the Path Difference
The path difference Δ between the two waves arriving at the point on the screen can be calculated using the formula:
Δ=b⋅xd
where x is the horizontal distance from the midpoint between the slits to the point on the screen. Since we are considering the point directly in front of one slit, x=0, and thus the path difference simplifies to:
Δ=b⋅0d=0
However, we need to consider the scenario where we look at points slightly off-center, leading to a path difference of:
Δ=bd⋅(b2)=b22d
This represents the path difference when considering the symmetry of the setup.
Step 4: Set Up the Condition for Destructive Interference
The condition for destructive interference is given by:
Δ=(n−12)λ
where n is an integer (1, 2, 3, ...).
Step 5: Equate the Path Difference to the Condition for Destructive Interference
Setting the two expressions for path difference equal gives:
b22d=(n−12)λ
Rearranging this gives:
λ=b2d⋅12n−1
Step 6: Identify the Missing Wavelengths
The wavelengths that are missing correspond to different values of n:
- For n=1:
λ1=b2d
- For n=2:
λ2=b23d
- For n=3:
λ3=b25d
- And so on...
Step 7: Conclude the Missing Wavelengths
The missing wavelengths at the point directly in front of one of the slits are:
λ=b2d,b23d,b25d,…
We have two slits separated by a distance b and a screen located at a distance d from the slits. The point of interest on the screen is directly in front of one of the slits.
At the point directly in front of one of the slits, certain wavelengths are missing due to destructive interference. For destructive interference to occur, the path difference between the light waves from the two slits must be an odd multiple of half the wavelength.
The path difference Δ between the two waves arriving at the point on the screen can be calculated using the formula:
Δ=b⋅xd
where x is the horizontal distance from the midpoint between the slits to the point on the screen. Since we are considering the point directly in front of one slit, x=0, and thus the path difference simplifies to:
Δ=b⋅0d=0
However, we need to consider the scenario where we look at points slightly off-center, leading to a path difference of:
Δ=bd⋅(b2)=b22d
This represents the path difference when considering the symmetry of the setup.
The condition for destructive interference is given by:
Δ=(n−12)λ
where n is an integer (1, 2, 3, ...).
Setting the two expressions for path difference equal gives:
b22d=(n−12)λ
Rearranging this gives:
λ=b2d⋅12n−1
The wavelengths that are missing correspond to different values of n:
- For n=1:
λ1=b2d
- For n=2:
λ2=b23d
- For n=3:
λ3=b25d
- And so on...
The missing wavelengths at the point directly in front of one of the slits are:
λ=b2d,b23d,b25d,…
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 1
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 2
2 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
White light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View Solution
Knowledge Check
In a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
AdλBλ2dDCD22λDDd22Dλ
At a point on the screen directly in front of one of the slits, find the missing wavelengths.
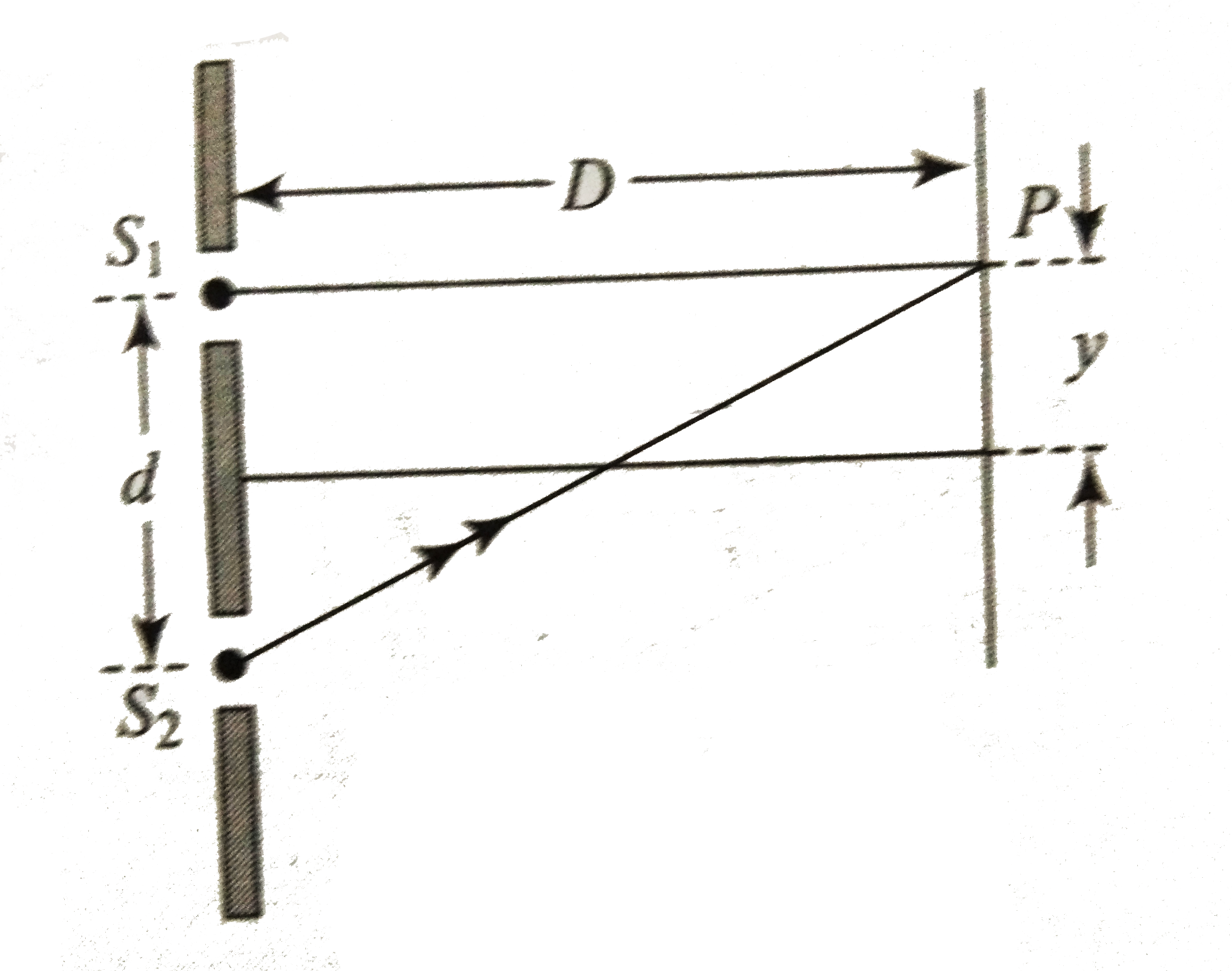
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionThe distance between the tew slits in a Young's double slit experiment is d and the distance of the screen from the plane of the slits is b, P is a point on the screen directly infront of one of the slits. The path difference between the waves arriving at P from the two slits is
View SolutionIn the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
View Solution
