Two coherent radio point sources that are separated by 2.0 m are radiating in phase with a wavelength of 0.25m. If a detector moves in a large circle around their mid-point. At how many points will the detector show a maximum signal?
The correct Answer is:B, C
To solve the problem of how many points a detector will show a maximum signal when moving in a large circle around two coherent radio point sources, we can follow these steps:
1. Identify the Given Values:
- Distance between the two sources (d) = 2.0 m
- Wavelength (λ) = 0.25 m
2. Understanding the Condition for Maximum Signal:
- For constructive interference (maximum signal), the path difference (Δx) between the waves from the two sources must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,3,…)
3. Calculate the Maximum Path Difference:
- The maximum path difference occurs when the detector is at the farthest points from the midpoint of the two sources. The maximum path difference can be calculated as:
Δxmax=d=2.0 m
4. Determine the Maximum Number of Wavelengths:
- To find how many wavelengths fit into the maximum path difference:
nmax=Δxmaxλ=2.0 m0.25 m=8
5. Count the Number of Maxima:
- The maxima occur at integer values of n from 0 to n_max. Therefore, the number of maxima is:
nmax+1=8+1=9
- However, since the detector moves in a circle, we need to consider the symmetry and the fact that maxima will occur on both sides of the midpoint. Thus, we will have:
Total Maxima=2×nmax+1=2×8+1=17
6. Final Count of Maxima:
- The total number of points where the detector will show a maximum signal is:
Total Maxima=17
Conclusion:
The detector will show a maximum signal at 17 points as it moves in a large circle around the midpoint of the two coherent radio point sources.
---
- Distance between the two sources (d) = 2.0 m
- Wavelength (λ) = 0.25 m
- For constructive interference (maximum signal), the path difference (Δx) between the waves from the two sources must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,3,…)
- The maximum path difference occurs when the detector is at the farthest points from the midpoint of the two sources. The maximum path difference can be calculated as:
Δxmax=d=2.0 m
- To find how many wavelengths fit into the maximum path difference:
nmax=Δxmaxλ=2.0 m0.25 m=8
- The maxima occur at integer values of n from 0 to n_max. Therefore, the number of maxima is:
nmax+1=8+1=9
- However, since the detector moves in a circle, we need to consider the symmetry and the fact that maxima will occur on both sides of the midpoint. Thus, we will have:
Total Maxima=2×nmax+1=2×8+1=17
- The total number of points where the detector will show a maximum signal is:
Total Maxima=17
The detector will show a maximum signal at 17 points as it moves in a large circle around the midpoint of the two coherent radio point sources.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Comprehensionn Based4videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
Two point sources separated by 2.0 m are radiating in phase with λ=0.50m. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?
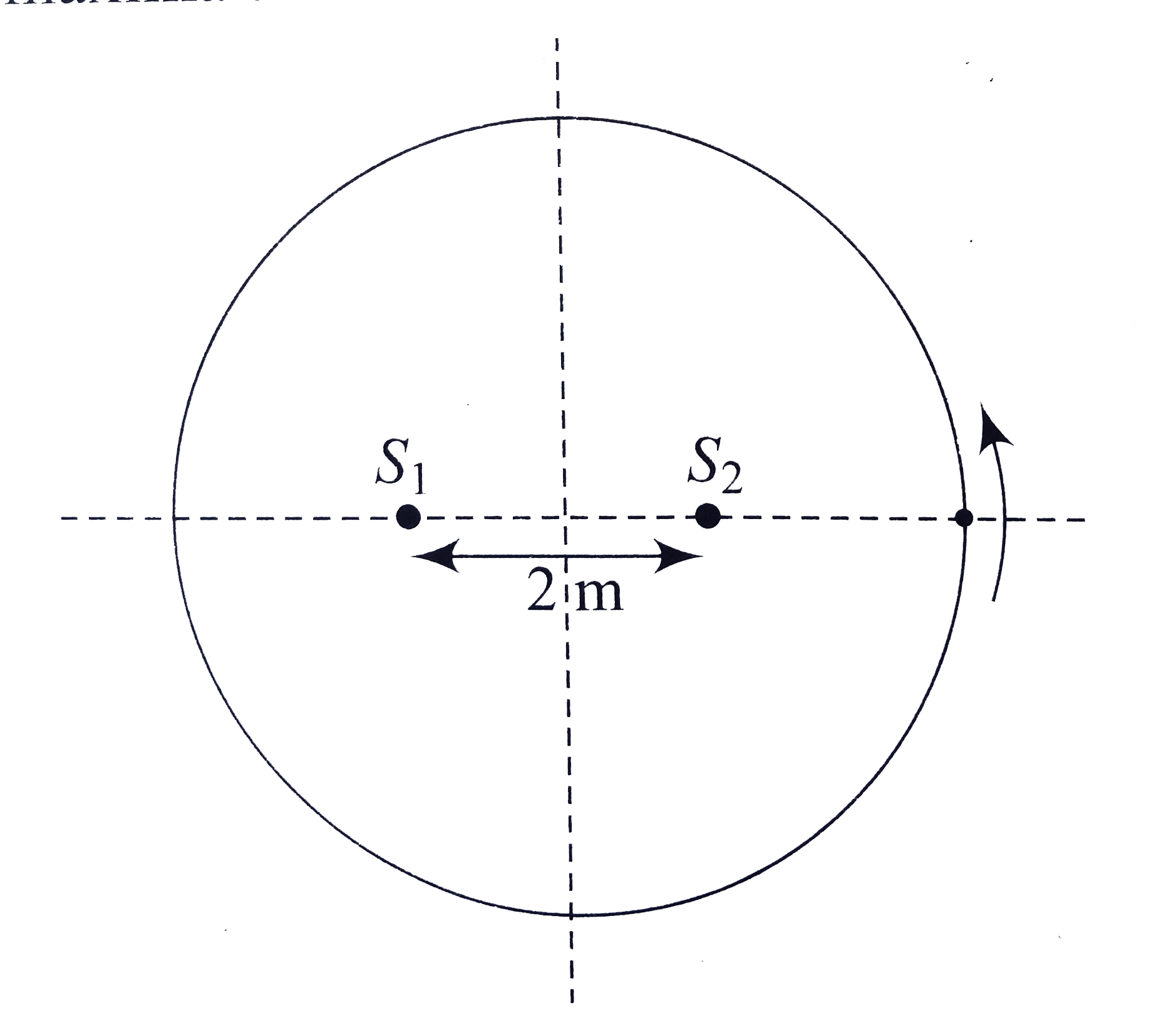 View Solution
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as
 View Solution
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 View Solution
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 View Solution
View Solution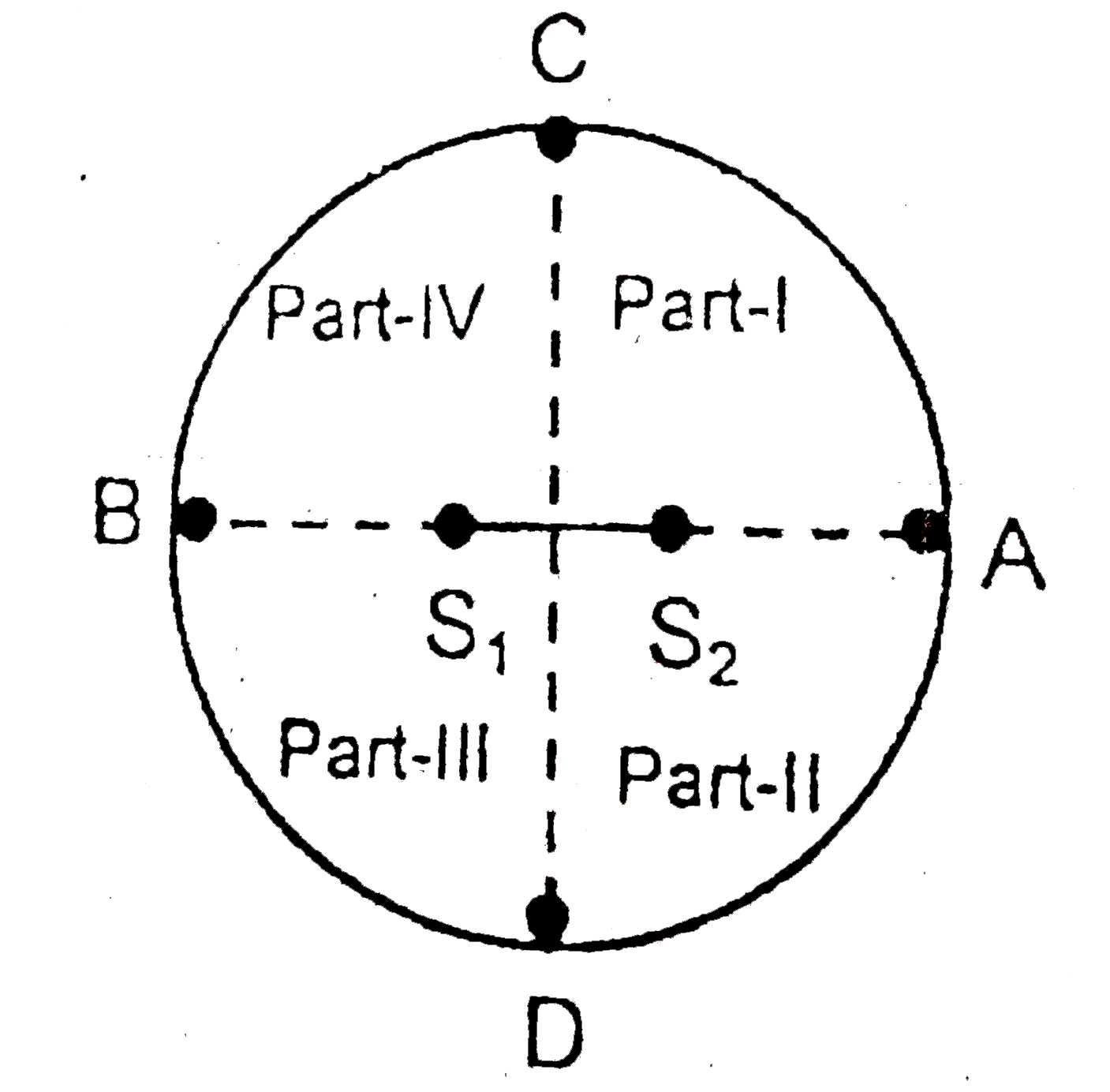
two sound sources S1 and S2 are kept symmetrically about the centre of a circle as shown. The circle is divided is 4 parts. Both the sources are separated by a 8λ/3 distance.
Where λ is wavelength of sound emitted by the sources. A detector is moving around the circle. How many times it will detect a minima in II part if S1 is leading S2 by phase of 2π/3?View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
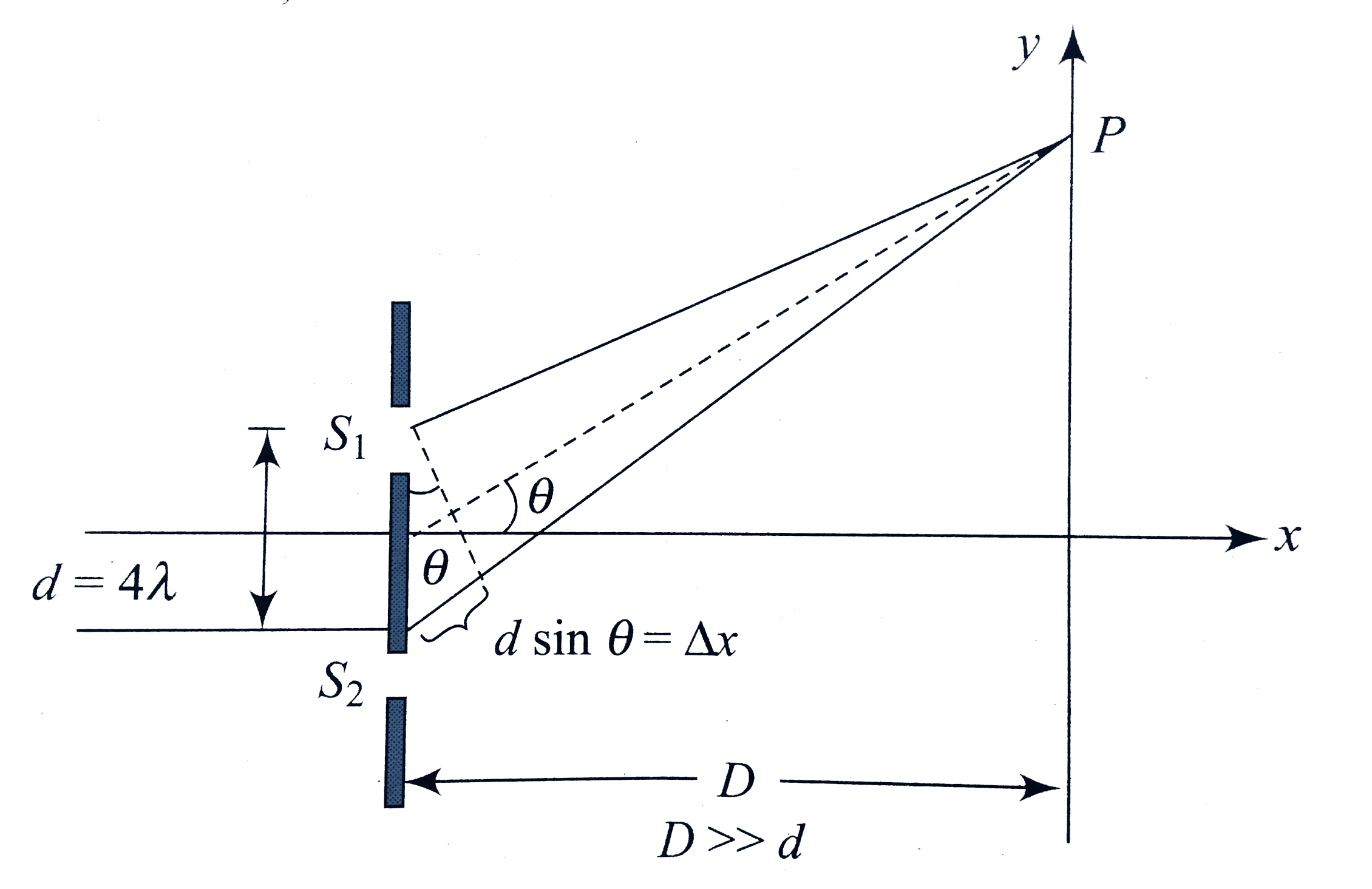
If a detector moves along the y-axis, what is the maximum number of minima observed?View SolutionTwo coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n
 View Solution
View Solution_E01_036_Q01.png)
Two point source separated by d=5μm emit light of wavelength λ=2μm in phase A cicular wire of radius 20μm is placed aournd the source as shown in figure.View Solution

