The radius of a thin wire is 0.16mm. The area of cross section taking significant figures into consideration in square millimeter is
0.0804
0.080
0.08
0.080384
The correct Answer is:C
To find the area of cross-section of a thin wire given its radius, we can follow these steps:
Step 1: Identify the formula for the area of a circle
The area A of a circle is calculated using the formula:
A=πr2
where r is the radius of the circle.
Step 2: Substitute the given radius into the formula
The radius of the wire is given as r=0.16mm. We can substitute this value into the formula:
A=π(0.16mm)2
Step 3: Calculate r2
First, we calculate (0.16mm)2:
(0.16)2=0.0256mm2
Step 4: Multiply by π
Now we multiply 0.0256mm2 by π (approximately 3.14159):
A=π×0.0256mm2≈3.14159×0.0256≈0.080384mm2
Step 5: Consider significant figures
The original radius 0.16mm has 2 significant figures. Therefore, our final answer for the area must also be expressed with 2 significant figures.
Step 6: Round the area to 2 significant figures
Rounding 0.080384mm2 to 2 significant figures gives us:
A≈0.08mm2
Final Answer
The area of cross-section of the wire, taking significant figures into consideration, is:
0.08mm2
---
The area A of a circle is calculated using the formula:
A=πr2
where r is the radius of the circle.
The radius of the wire is given as r=0.16mm. We can substitute this value into the formula:
A=π(0.16mm)2
First, we calculate (0.16mm)2:
(0.16)2=0.0256mm2
Now we multiply 0.0256mm2 by π (approximately 3.14159):
A=π×0.0256mm2≈3.14159×0.0256≈0.080384mm2
The original radius 0.16mm has 2 significant figures. Therefore, our final answer for the area must also be expressed with 2 significant figures.
Rounding 0.080384mm2 to 2 significant figures gives us:
A≈0.08mm2
The area of cross-section of the wire, taking significant figures into consideration, is:
0.08mm2
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
Knowledge Check
a thin slice is cut from a bagel, creating the cross - section represented below . The diameter of the bagel is 144 mm and the width from the inner edge of the bagel to the outer edge is uniformly 56 mm. Which of the following is closest to the area , in square millimeters , of the shaded empty space inside the cross -section of the bagel ?
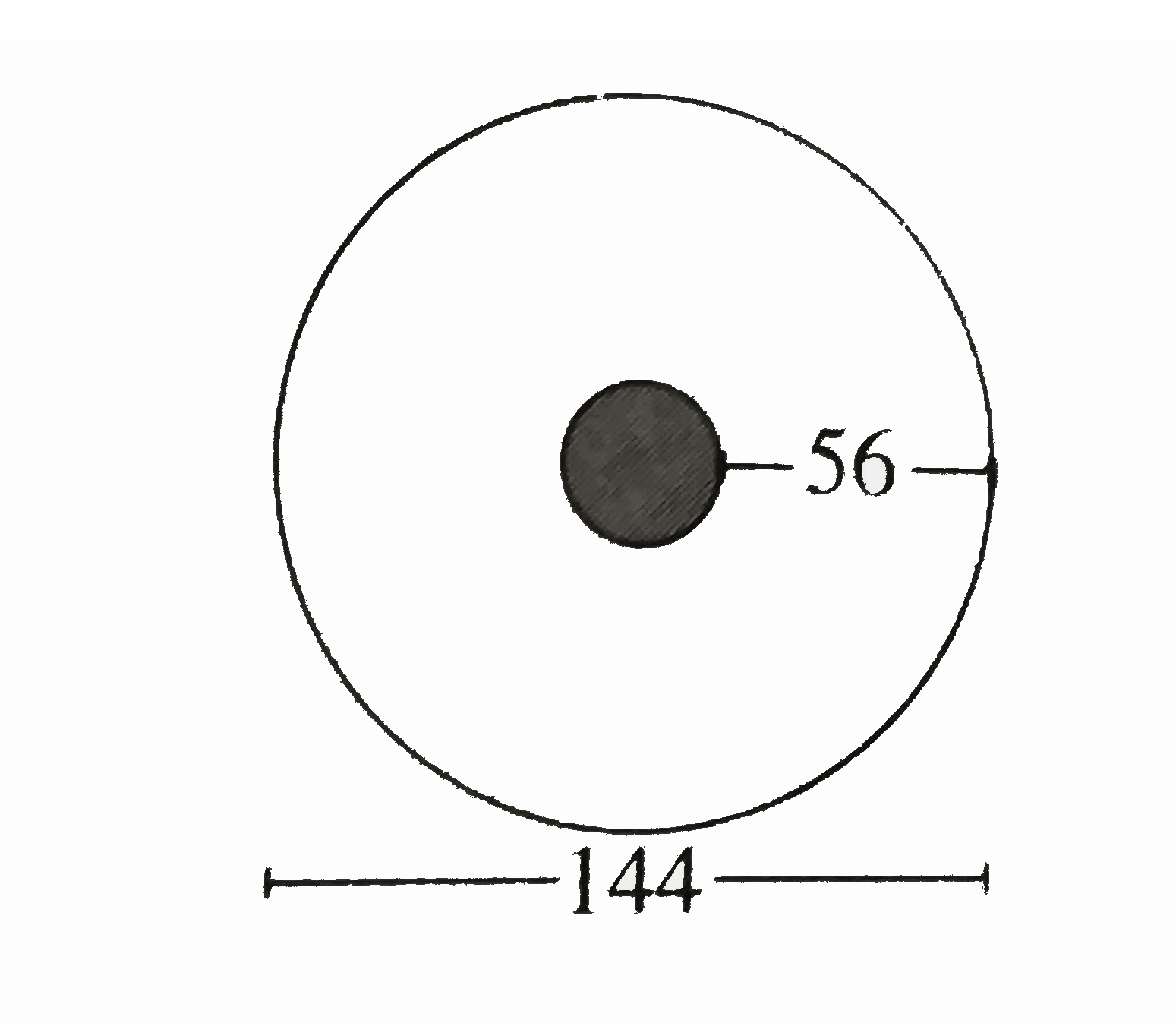 A100B450C800D3,200
A100B450C800D3,200The Poisson's ratio of a material is 0.4. If a force is applied to a wire of this material, there is a decrease of cross-sectional area by 2%. The percentage increase in its length is
A3%B2.5%C1%D0.5%
Considering a wire of non-uniform cross-section as shown.If the area of cross-section at A is double of the area of cross-section at point B.Ratio of heat energy dissipated in a unit volume per unit time at points A and B is
_PHY_E05_279_Q01.png)
View SolutionFrom some instruments current measured is I=10.0amp, potential different measured is V=100.0V, length of wire is 31.4cm, and diameter of wire is 2.00mm (all in correct significant figure). The resistivity of wire (in correct significant figures)will be (use π=3.14)
View SolutionA square loop of length L is made of wire of uniform cross-section carrying current l as shown in figure then magnetic field at centre of square is
View SolutionA very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is
View SolutionA wire of radius R having uniform cross section in which steady current l is flowing. Then
View SolutionWhen a force of 100 N is applied on a wire of uniform cross-section as shown in figure then length of wire is increased by 1 mm. Energy stored in the wire will be

View Solution
