A spring is placed between the jaws of screw gauge such that the spring is not all compressed. The main scale reads 2 division and circular scale reads 28 divisions. Now we turn the circular scale by 18∘ such that the spring is compessed. The circular scale has 200 divisions and the least count of the main scale is 1mm. What is the force exerted by the spring on the jaws if the spring constnat is 100N/m
4mN
3mN
5mN
7mN
The correct Answer is:C
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Understand the Given Information
- Main scale reading (MSR) = 2 divisions
- Circular scale reading (CSR) = 28 divisions
- Circular scale has 200 divisions
- Least count of the main scale = 1 mm
- Spring constant (k) = 100 N/m
- The circular scale is turned by 18 degrees.
Step 2: Calculate the Least Count
The least count (LC) of the screw gauge can be calculated using the formula:
Least Count=Smallest division on the main scaleTotal number of divisions on the circular scale
Here, the smallest division on the main scale is 1 mm, and the total number of divisions on the circular scale is 200.
Least Count=1 mm200=0.005 mm=5×10−3 mm
Step 3: Convert the Circular Scale Reading to mm
When the circular scale is turned by 18 degrees, the amount of compression (Δx) can be calculated as follows:
Δx=Least Count×(Angle turned360∘)
Substituting the values:
Δx=0.005 mm×(18360)=0.005 mm×120=0.00025 mm
Now, convert this to meters:
Δx=0.00025 mm×1 m1000 mm=0.00000025 m=2.5×10−4 m
Step 4: Calculate the Force Exerted by the Spring
The force exerted by the spring can be calculated using Hooke's Law:
F=k⋅Δx
Substituting the values:
F=100 N/m×2.5×10−4 m=0.025 N
Final Answer
The force exerted by the spring on the jaws is 0.025 N.
---
- Main scale reading (MSR) = 2 divisions
- Circular scale reading (CSR) = 28 divisions
- Circular scale has 200 divisions
- Least count of the main scale = 1 mm
- Spring constant (k) = 100 N/m
- The circular scale is turned by 18 degrees.
The least count (LC) of the screw gauge can be calculated using the formula:
Least Count=Smallest division on the main scaleTotal number of divisions on the circular scale
Here, the smallest division on the main scale is 1 mm, and the total number of divisions on the circular scale is 200.
When the circular scale is turned by 18 degrees, the amount of compression (Δx) can be calculated as follows:
Δx=Least Count×(Angle turned360∘)
Substituting the values:
Δx=0.005 mm×(18360)=0.005 mm×120=0.00025 mm
Now, convert this to meters:
Δx=0.00025 mm×1 m1000 mm=0.00000025 m=2.5×10−4 m
The force exerted by the spring can be calculated using Hooke's Law:
F=k⋅Δx
Substituting the values:
F=100 N/m×2.5×10−4 m=0.025 N
The force exerted by the spring on the jaws is 0.025 N.
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
The pitch of a screw gauge is 0.5 mm. It's head scale contains 50 divisions. The least count of the screw gauge is
View SolutionIn a screw gauge, 5 complete rotations of circular scale give 1.5 mm reading on pitch scale. Consider circular scale has 50 divisions. Least count of the screw gauge is
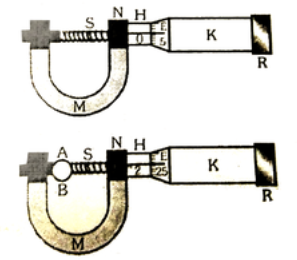
View SolutionThe circular scale of a screw gauge has 50. divisions and pitch of 0.5 mm. Main scale reading is 2. Find the diameter of sphere.
View SolutionA screw gauge advances by 3mm in 6 rotations. There are 50 divisions on circular scale. Find least count of screw gauge
View SolutionA screw gauge advances by 3mm in 6 rotations. There are 50 divisions on circular scale. Find least count of screw gauge
View SolutionThe figure shows the variation of energy with the orbit radius of a body in circular planetary motion.
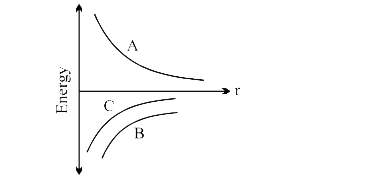
Find the correct statement about the curves A, B and C
View SolutionFind the thickness of the wire The main scale division is of 1mm In a complete rotation the screw advances by 1mm and the circular scale has 100 devisions

View SolutionThe given diagram represents a screw gauge. The circular scale is divided into 50 divisions and the linear scale is divided into millimeters. If the screw advances by 1mm when the circular scale makes 2 complete revolutions, find the least count of the instrument and the reading of the instrument in the figure.
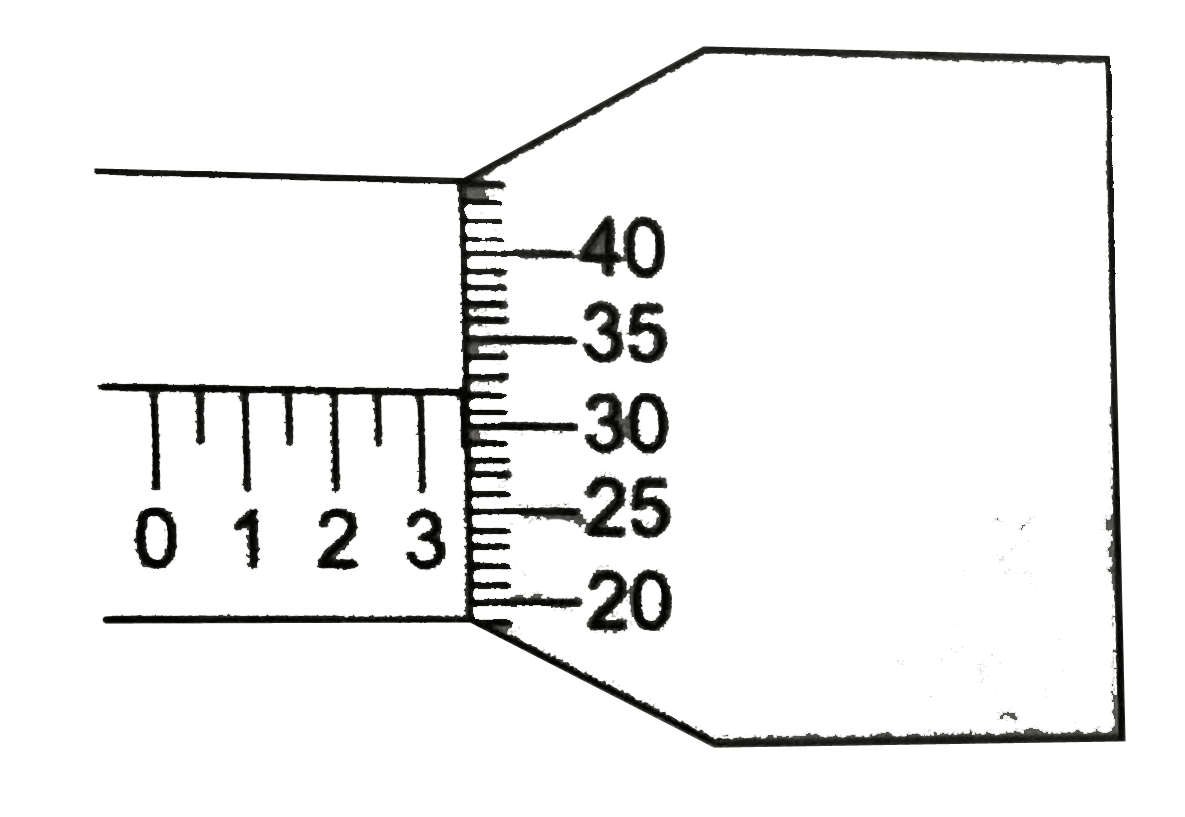 .
.
View SolutionA screw gauge has main scale divisions of 1 mm each and its circular scale has 50 division. While measuring the diameter of a ball, cap end is after 19th marking of main scale and 21st division of circular scale coincides with the reference line. What is the measured diameter diameter of the ball?
View SolutionThe pitch of a screw gauge is 1 mm and its circular scale has 100 divisions. In measurement of the diameter of a wire, the main scale reads 2 mm and 45th mark on circular scale coincides with the base line. Find the least count .
View Solution
