A body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity (s/v) varies with time t as


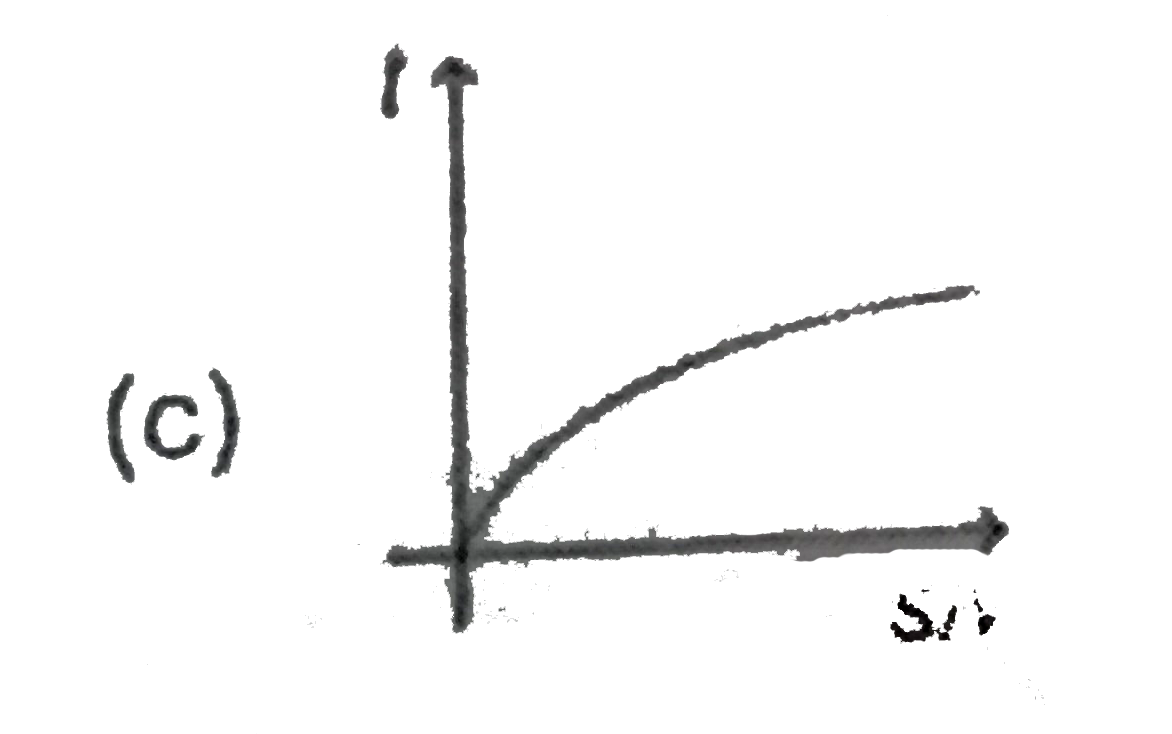
The correct Answer is:A
To solve the problem step by step, we will derive the relationship between displacement (s), velocity (v), and time (t) when a body is moved from rest by a machine delivering constant power.
Step 1: Understand the relationship between power, work, and time
Power (P) is defined as the rate of doing work. Mathematically, it can be expressed as:
P=Wt
Where W is the work done and t is the time taken. Rearranging gives us:
W=P⋅t
This is our Equation (1).
Step 2: Apply the work-energy theorem
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. Since the body starts from rest, the initial kinetic energy is zero. Thus, the work done can be expressed as:
W=ΔKE=12mv2−0=12mv2
This is our Equation (2).
Step 3: Equate the two expressions for work
From Equations (1) and (2), we can set them equal to each other:
12mv2=P⋅t
Rearranging this gives:
v2=2Ptm
Taking the square root of both sides, we find:
v=√2Ptm
This is our Equation (A).
Step 4: Relate displacement to time
Velocity (v) is defined as the rate of change of displacement (s) with respect to time (t):
v=dsdt
Substituting Equation (A) into this gives:
dsdt=√2Pm⋅t1/2
Rearranging gives:
ds=√2Pm⋅t1/2dt
Step 5: Integrate to find displacement
Integrating both sides, we have:
s=∫ds=∫√2Pm⋅t1/2dt
The constant can be factored out:
s=√2Pm⋅∫t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2
This is our Equation (B).
Step 6: Find the ratio of displacement to velocity
Now we need to find the ratio sv:
Using Equations (B) and (A):
sv=√2Pm⋅23t3/2√2Pm⋅t1/2
The √2Pm terms cancel out:
sv=23t3/2−1/2=23t1
Thus, we find:
sv=23t
Conclusion
The ratio of displacement to velocity sv varies linearly with time t.
Power (P) is defined as the rate of doing work. Mathematically, it can be expressed as:
P=Wt
Where W is the work done and t is the time taken. Rearranging gives us:
W=P⋅t
This is our Equation (1).
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. Since the body starts from rest, the initial kinetic energy is zero. Thus, the work done can be expressed as:
W=ΔKE=12mv2−0=12mv2
This is our Equation (2).
From Equations (1) and (2), we can set them equal to each other:
12mv2=P⋅t
Rearranging this gives:
v2=2Ptm
Taking the square root of both sides, we find:
v=√2Ptm
This is our Equation (A).
Velocity (v) is defined as the rate of change of displacement (s) with respect to time (t):
v=dsdt
Substituting Equation (A) into this gives:
dsdt=√2Pm⋅t1/2
Rearranging gives:
ds=√2Pm⋅t1/2dt
Integrating both sides, we have:
s=∫ds=∫√2Pm⋅t1/2dt
The constant can be factored out:
s=√2Pm⋅∫t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2
This is our Equation (B).
Now we need to find the ratio sv:
Using Equations (B) and (A):
sv=√2Pm⋅23t3/2√2Pm⋅t1/2
The √2Pm terms cancel out:
sv=23t3/2−1/2=23t1
Thus, we find:
sv=23t
The ratio of displacement to velocity sv varies linearly with time t.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering a power proportional to time (P∝t). Then, match the following.

View SolutionA car drives along a straight level frictionless road by an engine delivering constant power. Then velocity is directly proportional to
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t as
View Solution
