Two blocks A and B having different kinetic energies KA and KB(>KA) are released on rough horizontal ground. Coefficient of friction for both of them is same. Then
momentum of B is greater than momentum of A
more work has to be done by friction to stop B
B will travel more distance before stopping
from the given data we can not compare the distance travelled by them before stopping
The correct Answer is:B, D
To solve the problem step by step, we need to analyze the information given and apply the concepts of kinetic energy, friction, and motion.
Step 1: Understand the given information
We have two blocks, A and B, with kinetic energies KA and KB respectively, where KB>KA. Both blocks are placed on a rough horizontal surface with the same coefficient of friction.
Step 2: Analyze the kinetic energy
The kinetic energy of an object is given by the formula:
K=12mv2
where m is the mass and v is the velocity of the object. Since KB>KA, we can infer that block B has either a greater mass or a greater velocity (or both) compared to block A.
Step 3: Relate kinetic energy to momentum
The momentum P of an object is given by:
P=mv
From the kinetic energy expressions, we can express momentum in terms of kinetic energy:
KA=P2A2mAandKB=P2B2mB
This implies:
PA=√2KAmAandPB=√2KBmB
Step 4: Compare the momenta
Since we do not have a direct relation between the masses mA and mB, we cannot definitively conclude that PB>PA just because KB>KA. Therefore, we cannot say that the momentum of block B is greater than that of block A.
Step 5: Work done by friction
The work done by friction to stop an object is given by:
W=f⋅d
where f is the frictional force and d is the distance traveled before stopping. The frictional force f can be expressed as:
f=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity. Since both blocks have the same coefficient of friction, the work done by friction to stop block B will indeed be greater than that for block A, as block B has greater kinetic energy.
Step 6: Distance traveled before stopping
The distance d traveled before stopping can be calculated using the work-energy principle. The work done by friction is equal to the change in kinetic energy:
W=K−0=K
Thus, for block B, the distance it travels before stopping can be expressed as:
KB=μmBgdB
And for block A:
KA=μmAgdA
Since KB>KA, it follows that the work done by friction on block B is greater, indicating that it will travel a longer distance before stopping, but we cannot definitively compare the distances without knowing the masses.
Conclusion
- We cannot determine the relationship between the momenta of blocks A and B due to the lack of information about their masses.
- More work is done by friction to stop block B since it has greater kinetic energy.
- We cannot definitively conclude which block travels further before stopping without knowing the masses.
We have two blocks, A and B, with kinetic energies KA and KB respectively, where KB>KA. Both blocks are placed on a rough horizontal surface with the same coefficient of friction.
The kinetic energy of an object is given by the formula:
K=12mv2
where m is the mass and v is the velocity of the object. Since KB>KA, we can infer that block B has either a greater mass or a greater velocity (or both) compared to block A.
The momentum P of an object is given by:
P=mv
From the kinetic energy expressions, we can express momentum in terms of kinetic energy:
KA=P2A2mAandKB=P2B2mB
This implies:
PA=√2KAmAandPB=√2KBmB
Since we do not have a direct relation between the masses mA and mB, we cannot definitively conclude that PB>PA just because KB>KA. Therefore, we cannot say that the momentum of block B is greater than that of block A.
The work done by friction to stop an object is given by:
W=f⋅d
where f is the frictional force and d is the distance traveled before stopping. The frictional force f can be expressed as:
f=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity. Since both blocks have the same coefficient of friction, the work done by friction to stop block B will indeed be greater than that for block A, as block B has greater kinetic energy.
The distance d traveled before stopping can be calculated using the work-energy principle. The work done by friction is equal to the change in kinetic energy:
W=K−0=K
Thus, for block B, the distance it travels before stopping can be expressed as:
KB=μmBgdB
And for block A:
KA=μmAgdA
Since KB>KA, it follows that the work done by friction on block B is greater, indicating that it will travel a longer distance before stopping, but we cannot definitively compare the distances without knowing the masses.
- We cannot determine the relationship between the momenta of blocks A and B due to the lack of information about their masses.
- More work is done by friction to stop block B since it has greater kinetic energy.
- We cannot definitively conclude which block travels further before stopping without knowing the masses.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions
10 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Assertion: Two blocks of masses mA and mB (>mA are thrown towards each other with same speed over a rough ground. The coefficient of friction of both the blocks with ground is same. Initial velocity of CM is towards left.

Reason: Initial acceleration of center of mass is towards right.
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
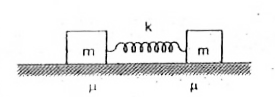
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
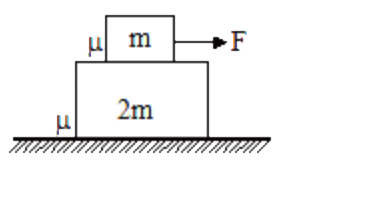
The system of two blocks is at rest an shown in the figure. A variable Horizontal force is applied to the upper block. The maximum possible constant force exerted by the horizontal ground surface on the lower block is ( coefficient of friction for both the contracts is μ )
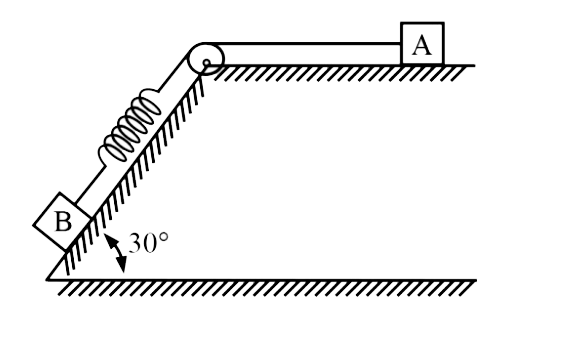
View SolutionA massless string and a spring connect two blocks A and B to each other. Block B slides over a frictionless inclined plane while block A slides over horizontal surface. Coefficient of friction between block a A horizontal surface is μ=0.2. At the instant shown blocks are moving with constant speed. Mass of block A and energy stored in spring the respectively. [g=10m/s2,k=1000Nm,mB=2kg]
View SolutionA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is

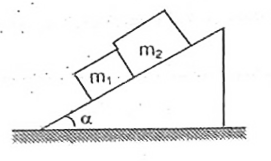
View SolutionTwo blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
View SolutionTwo identical blocks A and B, each of mass m=2kg are connected to the ends of an ideal spring having force constant K=1000Nm−1. System of these blocks and spring is placed on a rough floor. Coefficient of friction between blocks and floor is m=0.5. Block B is passed towards left so that spring gets compressed.
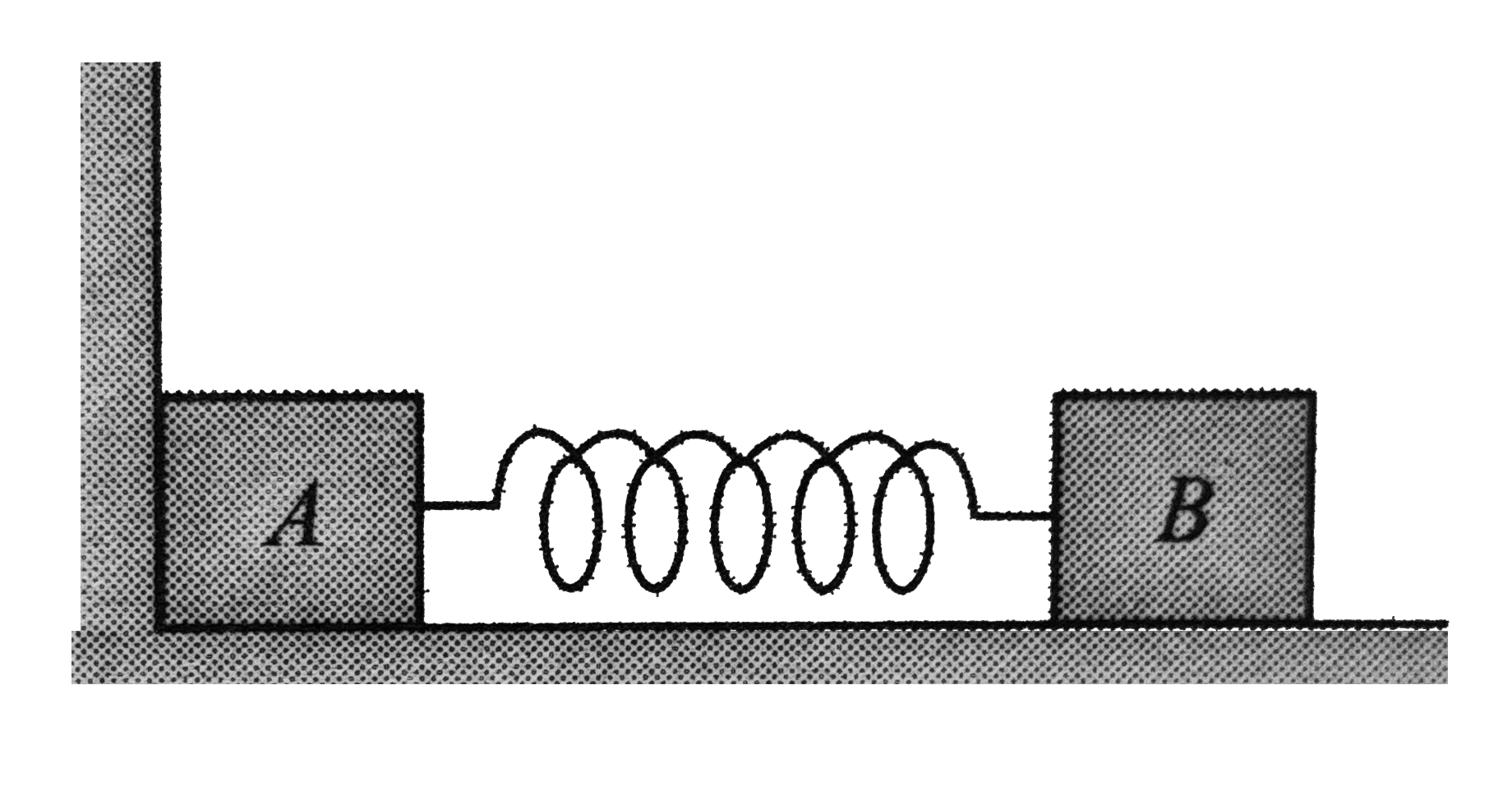
Calculate initial minimum compression x0 of spring such that block A leaves contact with the wall when system is released.
View SolutionTwo springs have their force constant as K1 and K2(K1<K2). When they are stretched by the same force:
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View Solution
