A bead slides on a fixed frictionless wire bent into a horizontal semicircle of radius R0 as shown in figure. In addition to any normal forces exerted by the wire, the bead is subjected to an external force that points directly away from origin and depends on distance r from the origin according to the formula F=F0(rR0)2ˆr
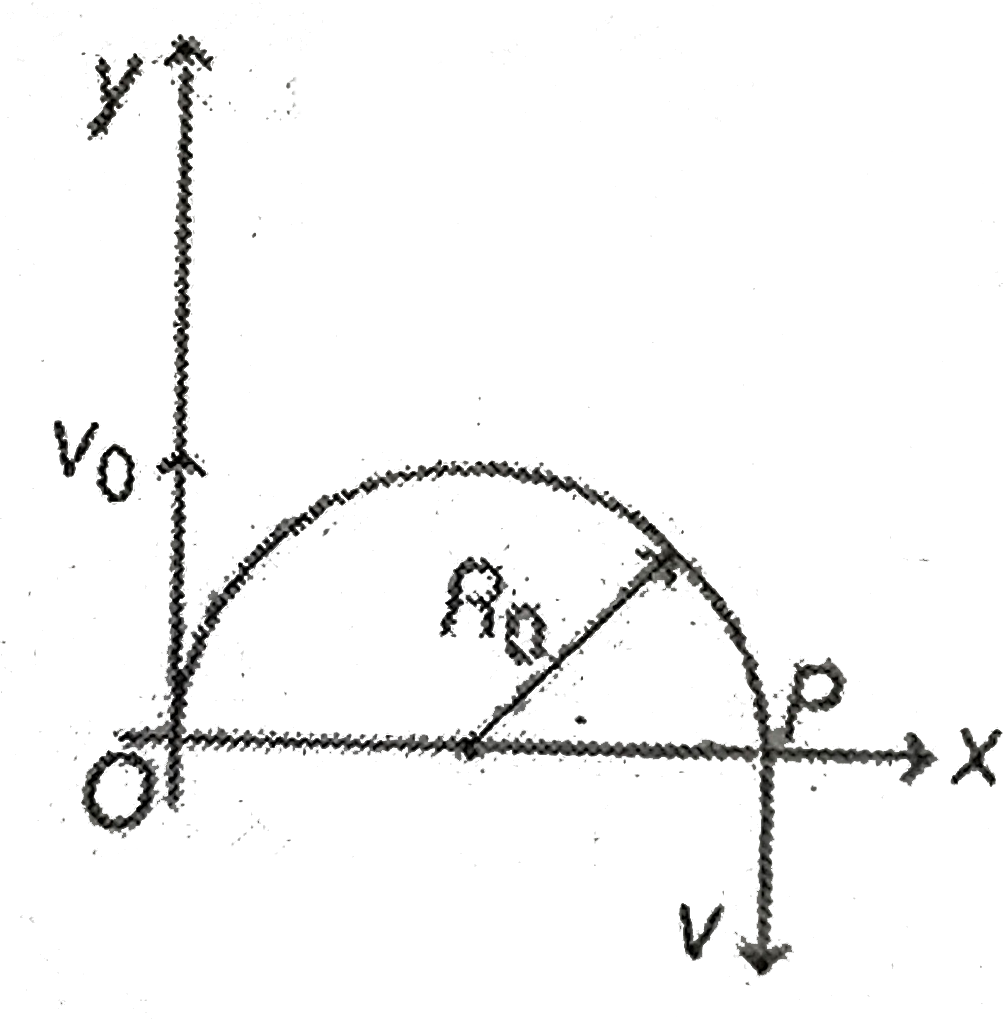
(a) Given force is a central force
(b) Given force is a conservation force
(c) Work done by external force as bead leaves the track (starting from origin) is 8F0R03
(d) Speed v of bead as it leaves the wire at P is √v20+18F0R03m
The correct Answer is:A, B, C
Step by step video & image solution for A bead slides on a fixed frictionless wire bent into a horizontal semicircle of radius R_(0) as shown in figure. In addition to any normal forces exerted by the wire, the bead is subjected to an external force that points directly away from origin and depends on distance r from the origin according to the formula F=F_(0)((r )/(R_(0)))^(2)hat(r) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions
10 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions

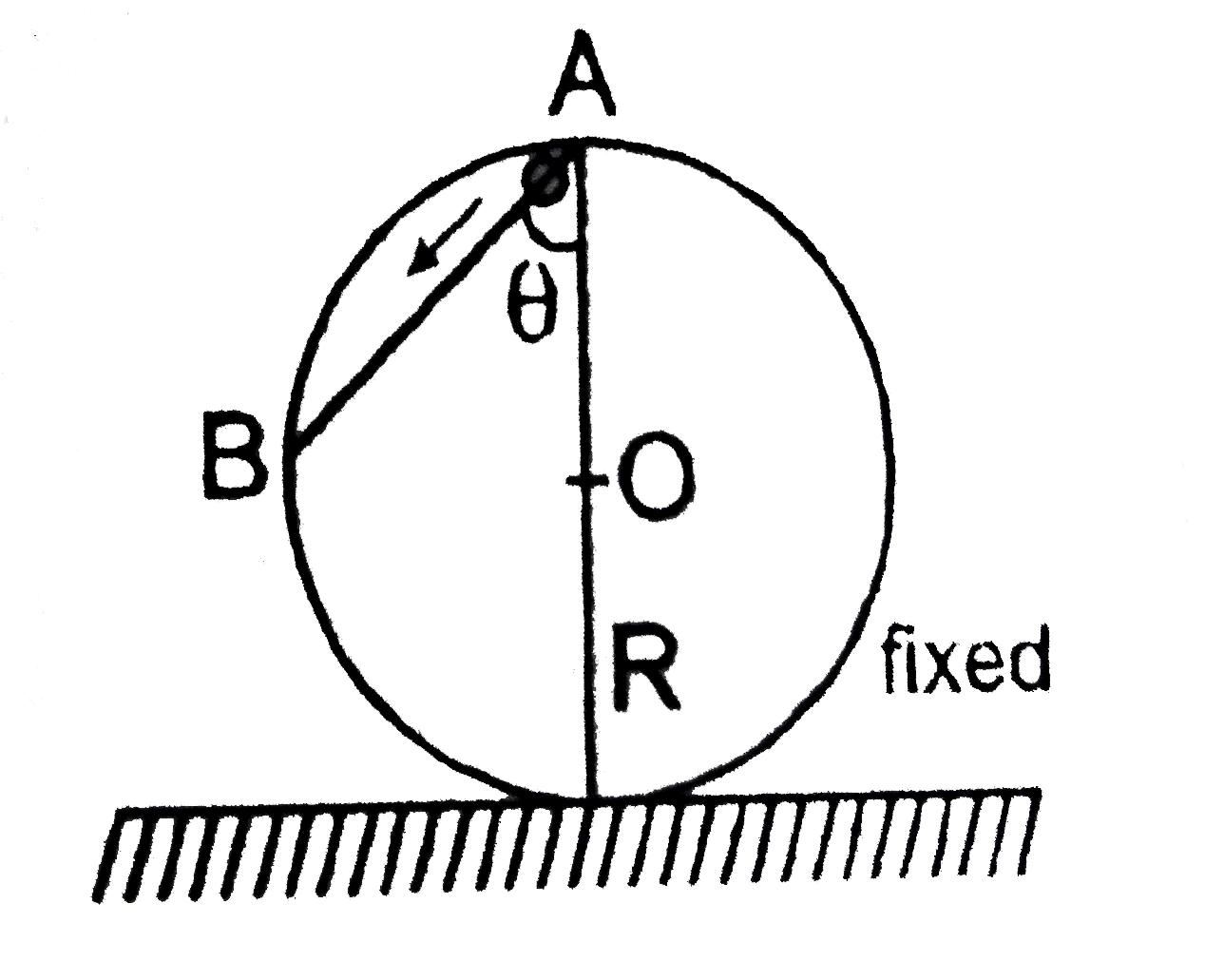
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.
View SolutionA frictionless wire is fixed between A and B inside of a hollow sphere of radius R as shown. A beam slips along the wire starting from the rest at point A. The time taken by the beam to slip from A to B will be
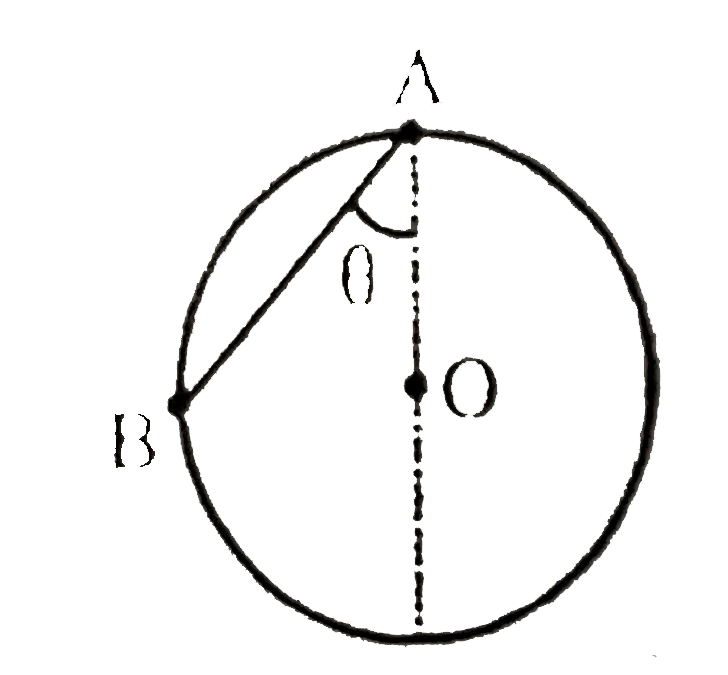
View SolutionA bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-
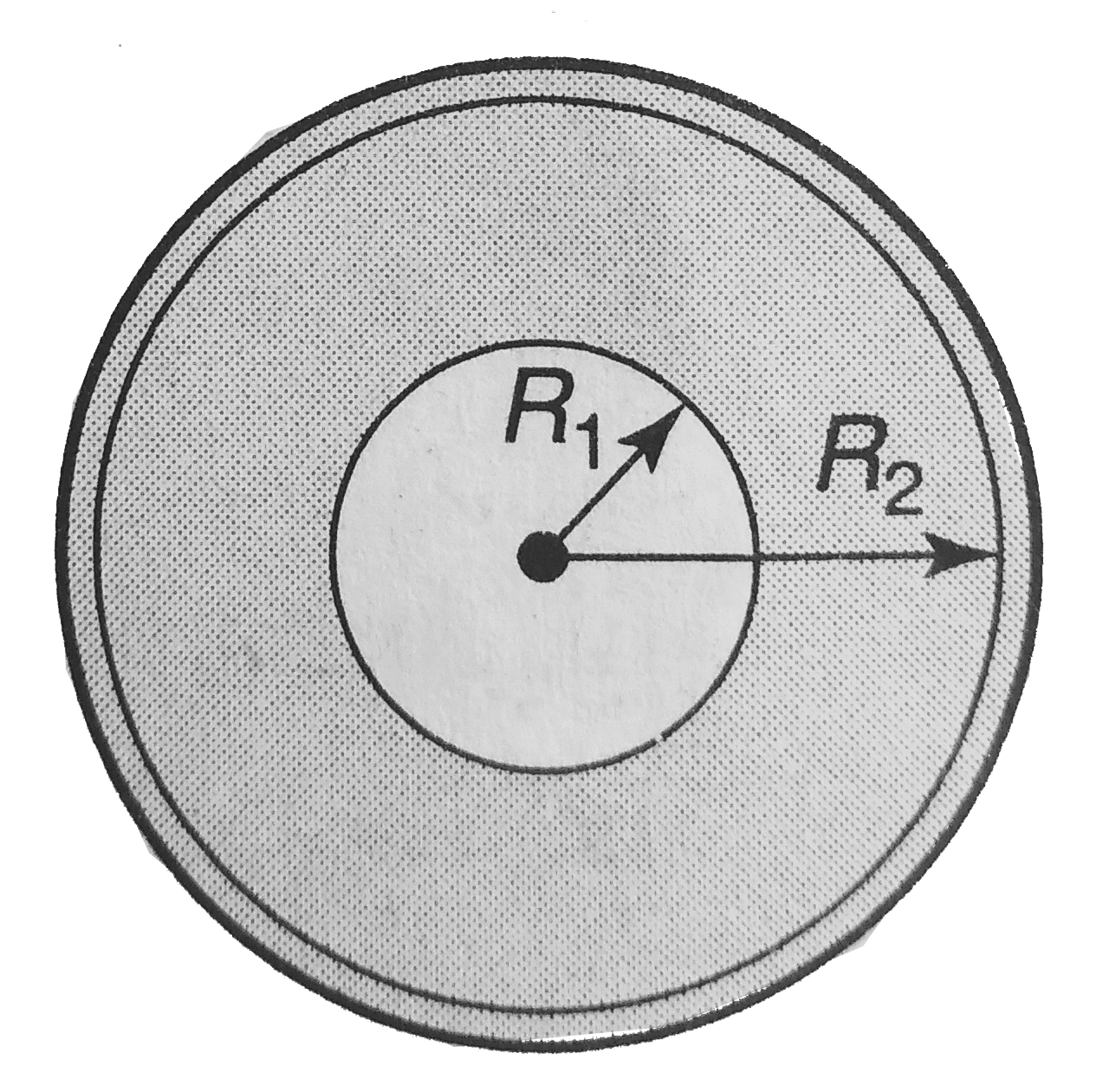
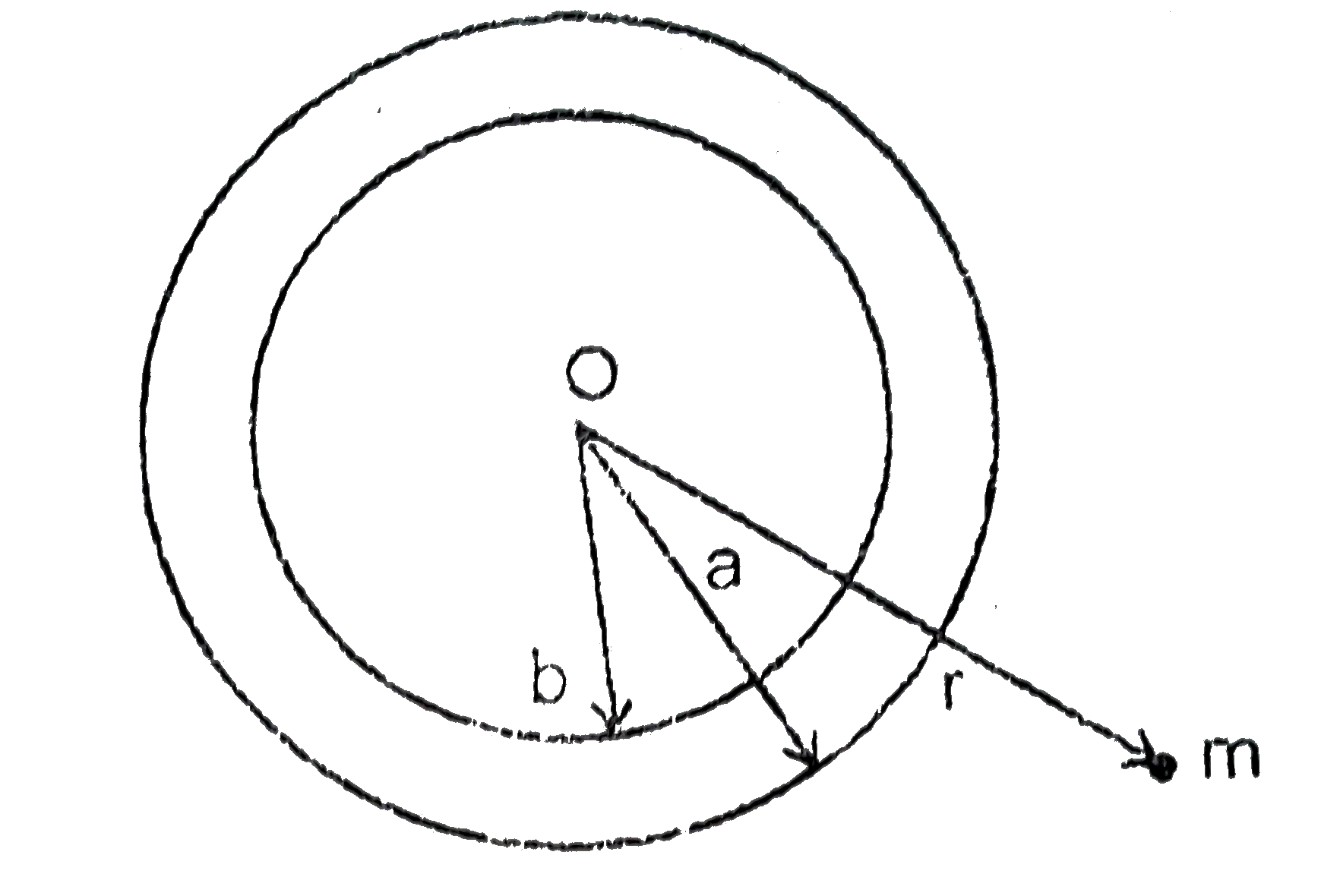
View SolutionA sphare of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
View SolutionA light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to

View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

View SolutionA sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,
,
View SolutionA bead of mass m is released from rest at A to move along the fixed smooth circular track as shown in figure. The ratio of magnitudes of centripetal force and normal reaction by the track on the bead at any point P0 described by the angle θ(≠0) would

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution
