A rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
zero
v1v1+v2l
v2lv1+v2
l2
The correct Answer is:B
To solve the problem of finding the distance of the instantaneous axis of rotation from v1 for a rod of length l giventwovelocities v_1 and v_2 at its ends in opposite directions, we can follow these steps:
1. Understand the Setup:
- We have a rod of length l.
- The left end of the rod has a velocity v1 and the right end has a velocity v2.
- The velocities are directed perpendicular to the length of the rod and in opposite directions.
2. Define the Instantaneous Axis of Rotation:
- Let the distance from the point where v1 is applied to the instantaneous axis of rotation be x.
- Consequently, the distance from the point where v2 is applied to the instantaneous axis of rotation will be l−x.
3. Relate Angular Velocities:
- The angular velocity ω about the instantaneous axis of rotation can be expressed for both ends of the rod:
- For the end with velocity v1:
ω=v1x
- For the end with velocity v2:
ω=v2l−x
4. Set the Angular Velocities Equal:
- Since both expressions represent the same angular velocity ω, we can set them equal to each other:
v1x=v2l−x
5. Cross-Multiply to Solve for x:
- Cross-multiplying gives:
v1(l−x)=v2x
- Expanding the left side:
v1l−v1x=v2x
6. Combine Like Terms:
- Rearranging the equation:
v1l=v1x+v2x
- Factoring out x:
v1l=x(v1+v2)
7. Solve for x:
- Finally, solve for x:
x=v1lv1+v2
Conclusion:
The distance of the instantaneous axis of rotation from v1 is given by:
x=v1lv1+v2
- We have a rod of length l.
- The left end of the rod has a velocity v1 and the right end has a velocity v2.
- The velocities are directed perpendicular to the length of the rod and in opposite directions.
- Let the distance from the point where v1 is applied to the instantaneous axis of rotation be x.
- Consequently, the distance from the point where v2 is applied to the instantaneous axis of rotation will be l−x.
- The angular velocity ω about the instantaneous axis of rotation can be expressed for both ends of the rod:
- For the end with velocity v1:
ω=v1x
- For the end with velocity v2:
ω=v2l−x
- Since both expressions represent the same angular velocity ω, we can set them equal to each other:
v1x=v2l−x
- Cross-multiplying gives:
v1(l−x)=v2x
- Expanding the left side:
v1l−v1x=v2x
- Rearranging the equation:
v1l=v1x+v2x
- Factoring out x:
v1l=x(v1+v2)
- Finally, solve for x:
x=v1lv1+v2
The distance of the instantaneous axis of rotation from v1 is given by:
x=v1lv1+v2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View SolutionShown in the figure is rod which moves with v=2ms−1 and rotates with ω=2πrads−1. Find the instantaneous axis of rotation.

View SolutionA homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
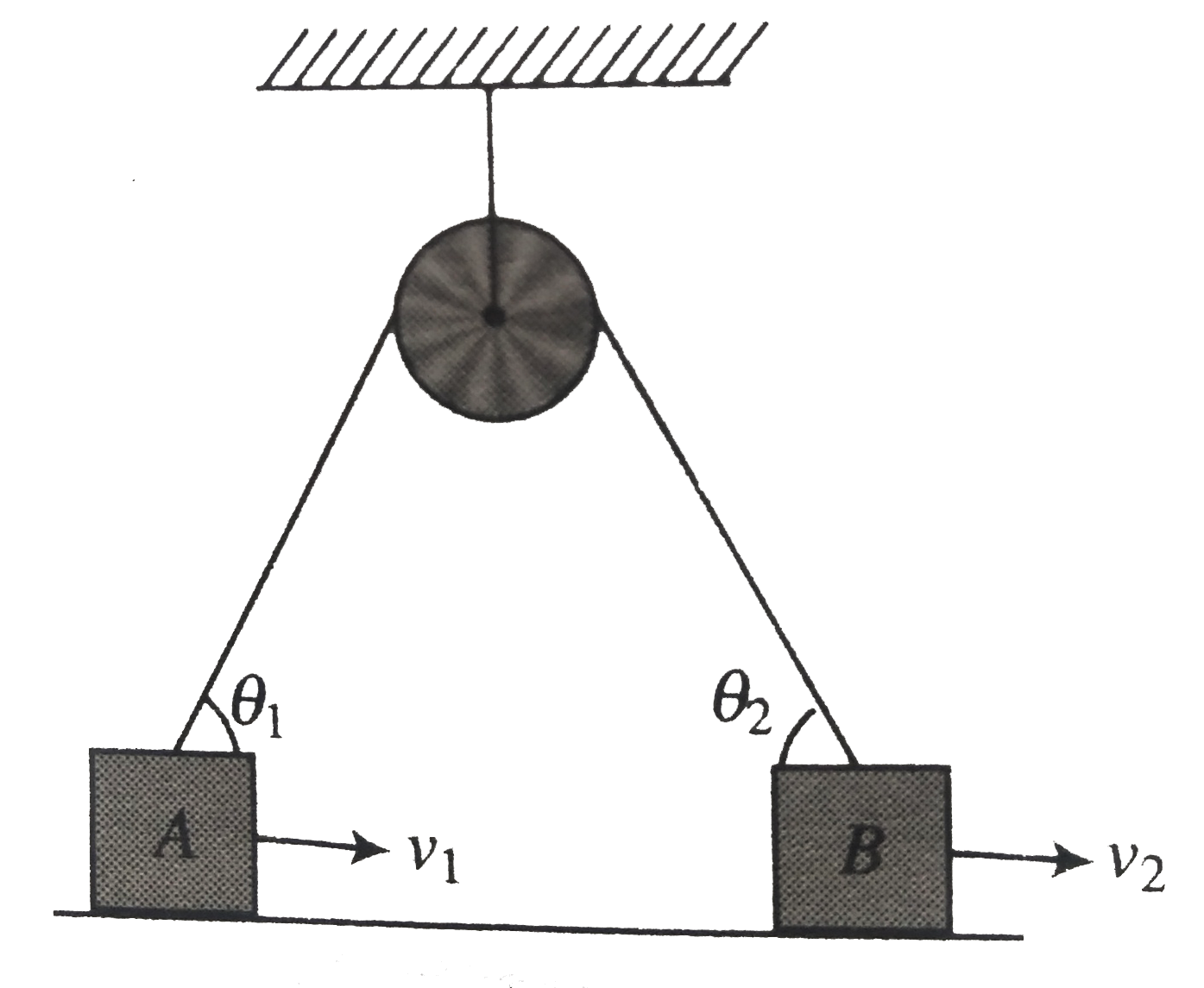
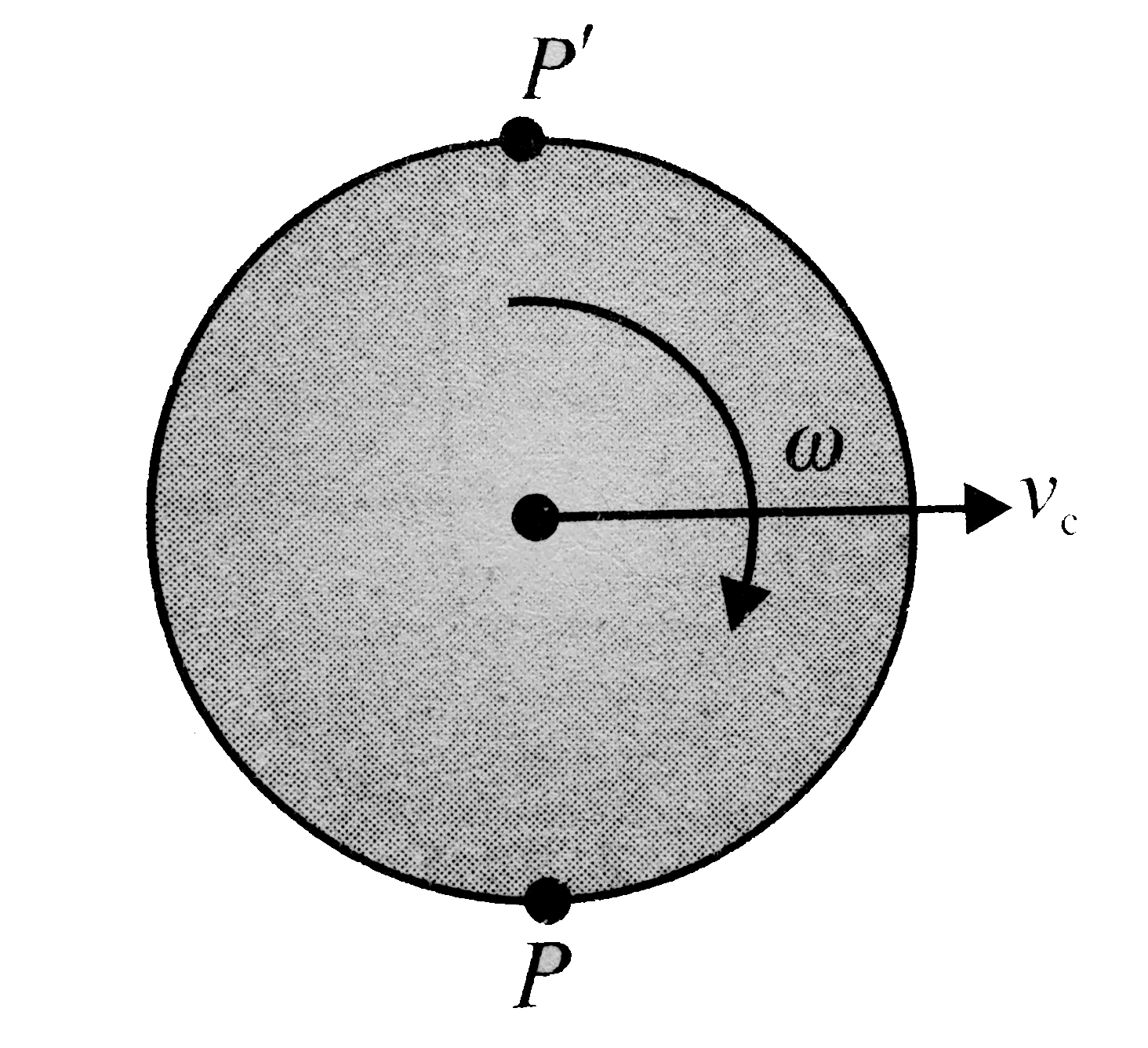
View SolutionA sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
View SolutionA rod of length L and mass M is acted on by two unequal force F1andF2(<F1) as shown in the following figure.

The tension in the rod at a distance y from the end a is given by
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View Solution
