Choose the correct option:
A wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximately
(a) 0.6ml2
(b) ml2
(c) 0.2ml2
(d) 0.4ml2
The correct Answer is:D
To find the moment of inertia of a wire bent in the form of a quarter circle about an axis passing through the center of the quarter circle, we can follow these steps:
1. Understanding the Problem:
- We have a wire of mass m and length l bent into the shape of a quarter circle.
- We need to find the moment of inertia of this quarter circle about an axis passing through its center.
2. Visualizing the Quarter Circle:
- Imagine that the quarter circle is part of a complete circle. If we were to complete the circle, it would consist of four identical quarter circles.
3. Moment of Inertia of a Full Circle:
- The moment of inertia I of a thin ring (or circle) about an axis through its center is given by:
I=mr22
- For a complete circle made of four quarter circles, the total moment of inertia would be:
Itotal=4×mr22=2mr2
4. Finding the Radius:
- The length of the quarter circle is equal to the arc length, which is given by:
l=14×2πr=πr2
- Rearranging this gives:
r=2lπ
5. Substituting the Radius:
- Now, substitute r back into the moment of inertia formula for the full circle:
Itotal=2m(2lπ)2
- Simplifying this:
Itotal=2m⋅4l2π2=8ml2π2
6. Moment of Inertia of the Quarter Circle:
- The moment of inertia of the quarter circle IQ is one-fourth of the total moment of inertia:
IQ=14Itotal=14⋅8ml2π2=2ml2π2
7. Approximation:
- To find the approximate value, we can use π≈3.14:
2ml2π2≈2ml2(3.14)2≈2ml29.86≈0.202ml2
- Thus, we can approximate IQ≈0.2ml2.
8. Final Answer:
- Therefore, the moment of inertia of the wire about the axis passing through the center of the quarter circle is approximately:
0.2ml2
- We have a wire of mass m and length l bent into the shape of a quarter circle.
- We need to find the moment of inertia of this quarter circle about an axis passing through its center.
- Imagine that the quarter circle is part of a complete circle. If we were to complete the circle, it would consist of four identical quarter circles.
- The moment of inertia I of a thin ring (or circle) about an axis through its center is given by:
I=mr22
- For a complete circle made of four quarter circles, the total moment of inertia would be:
Itotal=4×mr22=2mr2
- The length of the quarter circle is equal to the arc length, which is given by:
l=14×2πr=πr2
- Rearranging this gives:
r=2lπ
- Now, substitute r back into the moment of inertia formula for the full circle:
Itotal=2m(2lπ)2
- Simplifying this:
Itotal=2m⋅4l2π2=8ml2π2
- The moment of inertia of the quarter circle IQ is one-fourth of the total moment of inertia:
IQ=14Itotal=14⋅8ml2π2=2ml2π2
- To find the approximate value, we can use π≈3.14:
2ml2π2≈2ml2(3.14)2≈2ml29.86≈0.202ml2
- Thus, we can approximate IQ≈0.2ml2.
- Therefore, the moment of inertia of the wire about the axis passing through the center of the quarter circle is approximately:
0.2ml2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionA rod of mass 3 kg and of length 3m is bent in the form of an equilateral triangle. The moment of inertia of the triangle about a vertical axis perpendicular to plane and passing through centre of mass is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionFour rods of equal mass m and length L. Forms a square ABCD as shown in figure. The moment of inertia of ABCD about the axis OO' passing through the point A is
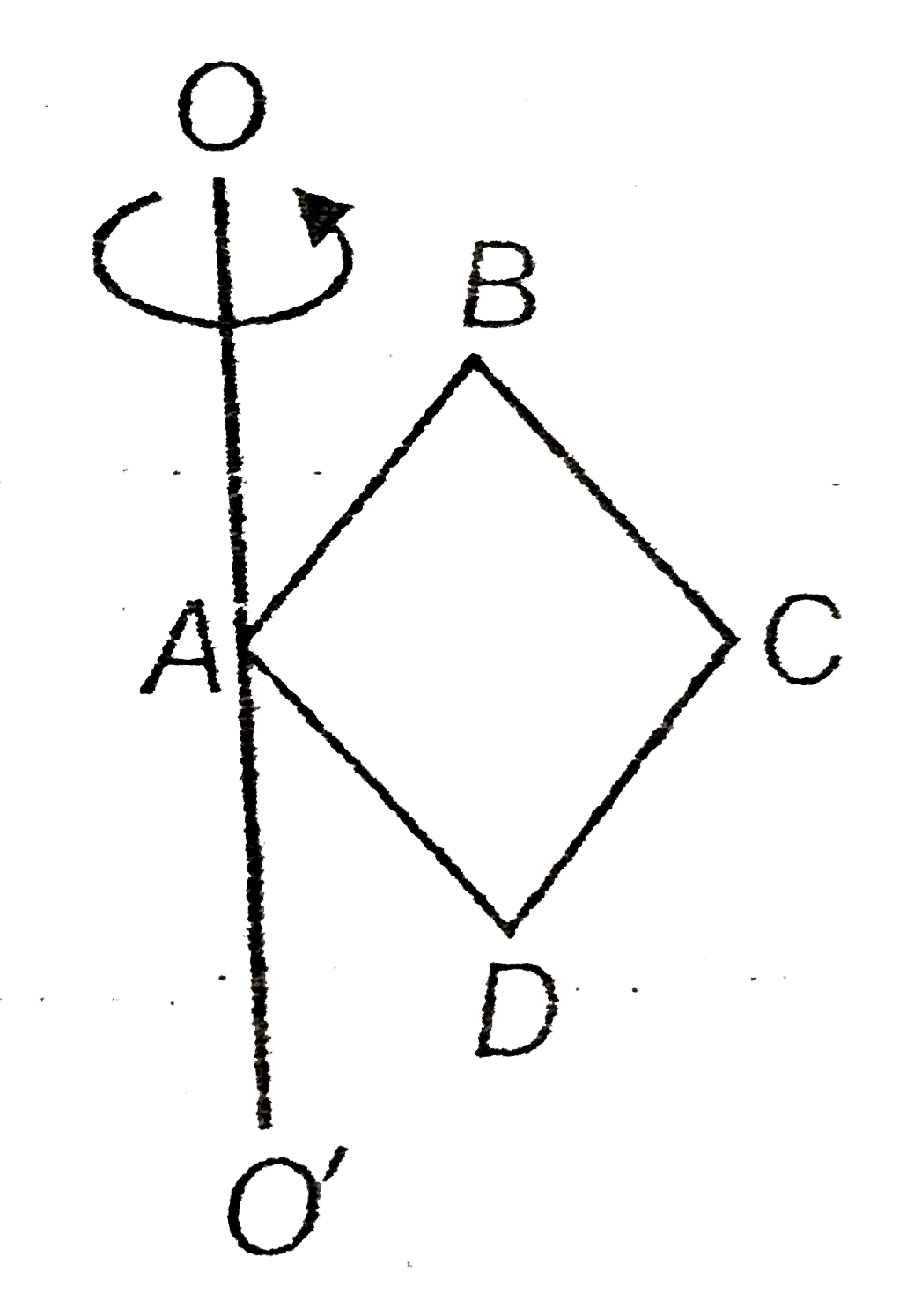
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionA wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
View SolutionA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is

View Solution
