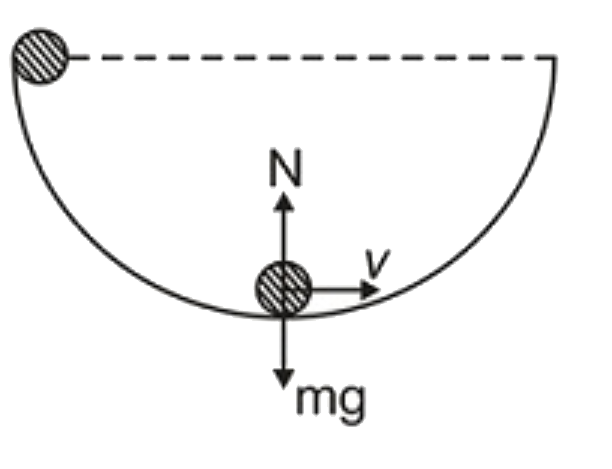
In the above probllem, the normal force between the ball and the shell in position B is (m=mass of ball)
127mg
79mg
177mg
107mg
The correct Answer is:C
To solve the problem regarding the normal force between the ball and the shell in position B, we can follow these steps:
1. Identify the Energy at Point A:
At point A, the ball is at a height h=r (where r is the radius of the shell). The potential energy at this point is given by:
PEA=mgh=mg⋅r
2. Identify the Energy at Point B:
At point B, the ball is at the bottom of the shell. The total mechanical energy at this point consists of both translational and rotational kinetic energy. The translational kinetic energy is given by 12mv2 and the rotational kinetic energy for a solid sphere is given by 12Iω2. The moment of inertia I for a solid sphere is 25mr2, and since ω=vr, we can express the rotational kinetic energy as:
KErot=12⋅25mr2⋅(vr)2=15mv2
Therefore, the total energy at point B is:
KEB=12mv2+15mv2=710mv2
3. Conservation of Energy:
Since energy is conserved, we can equate the potential energy at point A to the total kinetic energy at point B:
mgr=710mv2
Simplifying this equation (and canceling m):
gr=710v2
Rearranging gives:
v2=107gr
4. Centripetal Force Calculation:
At point B, the ball is moving in a circular path, and the net force towards the center (centripetal force) is provided by the normal force N and the weight of the ball mg. Therefore, we can write:
N−mg=mv2r
Substituting v2 from the previous step:
N−mg=m⋅107grr
Simplifying gives:
N−mg=107mg
Rearranging this equation to solve for N:
N=mg+107mg=77mg+107mg=177mg
5. Final Result:
The normal force between the ball and the shell in position B is:
N=177mg
At point A, the ball is at a height h=r (where r is the radius of the shell). The potential energy at this point is given by:
PEA=mgh=mg⋅r
At point B, the ball is at the bottom of the shell. The total mechanical energy at this point consists of both translational and rotational kinetic energy. The translational kinetic energy is given by 12mv2 and the rotational kinetic energy for a solid sphere is given by 12Iω2. The moment of inertia I for a solid sphere is 25mr2, and since ω=vr, we can express the rotational kinetic energy as:
KErot=12⋅25mr2⋅(vr)2=15mv2
Therefore, the total energy at point B is:
KEB=12mv2+15mv2=710mv2
Since energy is conserved, we can equate the potential energy at point A to the total kinetic energy at point B:
mgr=710mv2
Simplifying this equation (and canceling m):
gr=710v2
Rearranging gives:
v2=107gr
At point B, the ball is moving in a circular path, and the net force towards the center (centripetal force) is provided by the normal force N and the weight of the ball mg. Therefore, we can write:
N−mg=mv2r
Substituting v2 from the previous step:
N−mg=m⋅107grr
Simplifying gives:
N−mg=107mg
Rearranging this equation to solve for N:
N=mg+107mg=77mg+107mg=177mg
The normal force between the ball and the shell in position B is:
N=177mg
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A solid spherical ball of mass m is released from the topmost point of the shown semi - spherical shell. The track is sufficiently rough to enablle to enable pure rolling motion. The normal force between the ball and the shell at the lowest position is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA rubber ball of mass 50 g falls from a height of 5m and rebounds to a height of 1.25 m. Find the impulse and the average force between the ball and the ground if the time for which they are in contact was 0.1s

View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
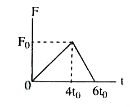
Maximum force exerted by the bat on the ball is
View SolutionA ball of mass 1 kg is released from position A inside a wedge with a hemispherical cut of radius 0.5 m as shown in figure. The force exerted by the wedge on ball, when the ball is in position B is (neglect friction everywhere) (Take g=10m/s2)

View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown

The speed of the ball at the instant the force acting on the ball is maximum is
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
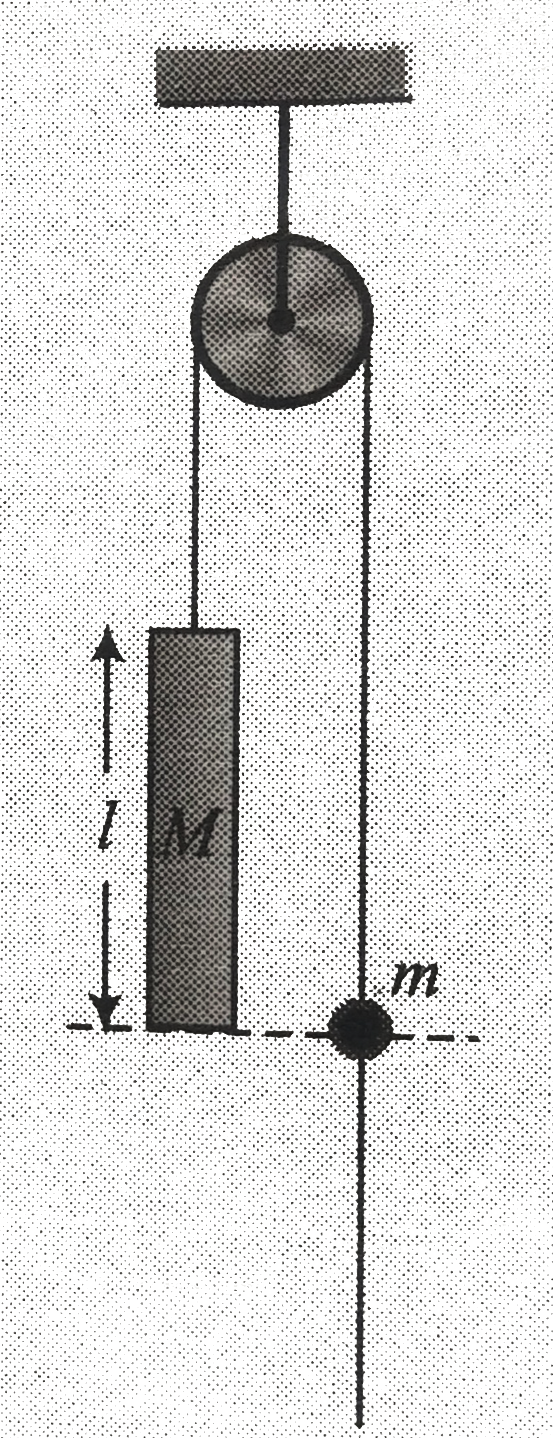
View SolutionTwo identical small conducting balls have positive charges q1 and q2 respectively. The force between the balls when they are placed at a separation is F. The balls are brought together so that they touch and then put back in their original positions. Prove that the force between the balls now, cannot be less than F.
View Solution
