A wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
11252ml2
8203ml2
5136ml2
7162ml2
The correct Answer is:D
To find the moment of inertia of a wire frame bent in the form of a rectangle ABCD about the side BC, we can follow these steps:
Step 1: Define the dimensions of the rectangle
Given that ABBC=2, we can let:
- BC=x
- AB=2x
Since ABCD is a rectangle, the opposite sides are equal:
- AD=BC=x
- CD=AB=2x
Step 2: Calculate the total length of the wire
The total length l of the wire frame is the sum of the lengths of all sides:
l=AB+BC+CD+AD=2x+x+2x+x=6x
From this, we can express x in terms of l:
x=l6
Step 3: Determine the mass distribution
The mass of the wire is uniformly distributed. Since the length of each side is proportional to its mass, we can find the mass of each side:
- Length of AB=CD=2x=2l6=l3
- Length of BC=AD=x=l6
Using the ratio of lengths to find mass:
- Mass of AB=CD=m3 (since they are each l3 of the total length)
- Mass of BC=AD=m6 (since they are each l6 of the total length)
Step 4: Calculate the moment of inertia for each side about BC
1. For sides AB and CD:
The moment of inertia of a rod about an axis through one end is given by:
I=13mL2
For AB and CD:
- Length L=l3
- Mass m=m3
Thus, the moment of inertia for each side is:
IAB=ICD=13(m3)(l3)2=13⋅m3⋅l29=ml281
2. For side AD:
The moment of inertia for side AD about BC:
- Length L=l6
- Mass m=m6
Thus, the moment of inertia is:
IAD=13(m6)(l6)2=13⋅m6⋅l236=ml2648
Step 5: Calculate the total moment of inertia about BC
Now, we sum the moments of inertia of all sides:
Itotal=IAB+ICD+IAD=ml281+ml281+ml254
To add these fractions, we need a common denominator. The least common multiple of 81 and 54 is 162:
Itotal=2ml281+3ml2162=4ml2162+3ml2162=7ml2162
Final Answer
Thus, the moment of inertia of the wire frame about the side BC is:
7ml2162
Given that ABBC=2, we can let:
- BC=x
- AB=2x
- AD=BC=x
- CD=AB=2x
The total length l of the wire frame is the sum of the lengths of all sides:
l=AB+BC+CD+AD=2x+x+2x+x=6x
From this, we can express x in terms of l:
x=l6
The mass of the wire is uniformly distributed. Since the length of each side is proportional to its mass, we can find the mass of each side:
- Length of AB=CD=2x=2l6=l3
- Length of BC=AD=x=l6
- Mass of AB=CD=m3 (since they are each l3 of the total length)
- Mass of BC=AD=m6 (since they are each l6 of the total length)
1. For sides AB and CD:
The moment of inertia of a rod about an axis through one end is given by:
I=13mL2
For AB and CD:
- Length L=l3
- Mass m=m3
IAB=ICD=13(m3)(l3)2=13⋅m3⋅l29=ml281
The moment of inertia for side AD about BC:
- Length L=l6
- Mass m=m6
IAD=13(m6)(l6)2=13⋅m6⋅l236=ml2648
Now, we sum the moments of inertia of all sides:
Itotal=IAB+ICD+IAD=ml281+ml281+ml254
Itotal=2ml281+3ml2162=4ml2162+3ml2162=7ml2162
Thus, the moment of inertia of the wire frame about the side BC is:
7ml2162
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be

View SolutionA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is

View Solution
Knowledge Check
IN a retangle ABCD (BC = 2AB). The moment of inertia along which aixs will be minimum
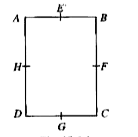 ABCBBDCHFDEG
ABCBBDCHFDEGA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 Aml2BzeroCml2π2Dml22π2
Aml2BzeroCml2π2Dml22π2
In a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
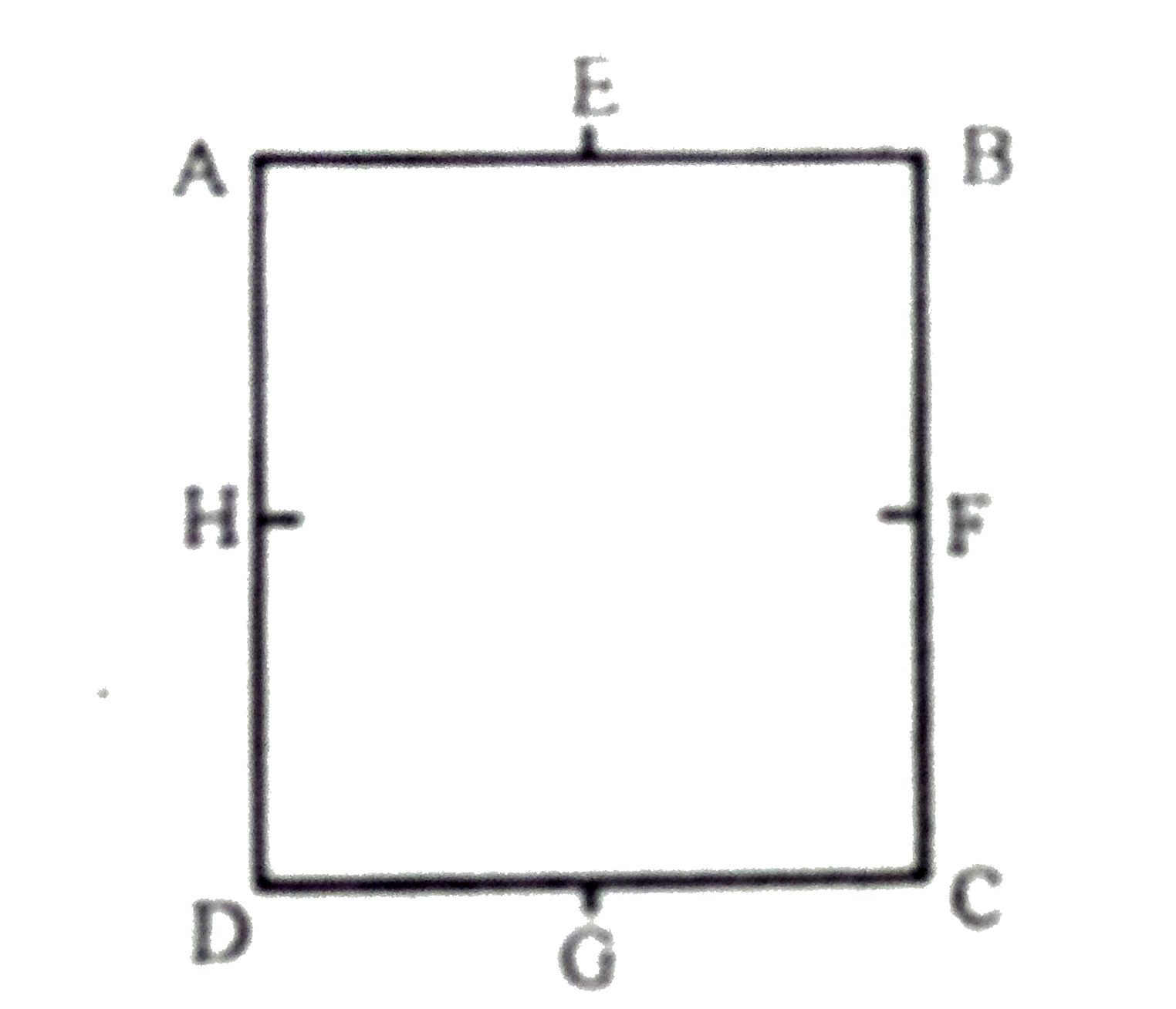
A. EG
B. HF
C. BD
D. BC
View SolutionChoose the correct option:
A wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximately
View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View SolutionChoose the correct option:
A wire of length l and mass m is first bent in a circle, then in a square and then in an equilateral triangle. The moment of inertia in these three cases about an axis perpendicular to their planes and passing through their centre of mass are I1,I2 and I3 respectively. Then maximum of them is
View SolutionAn iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 45∘. The moment of inertia of the bent rod about the same axis would be
View Solution
