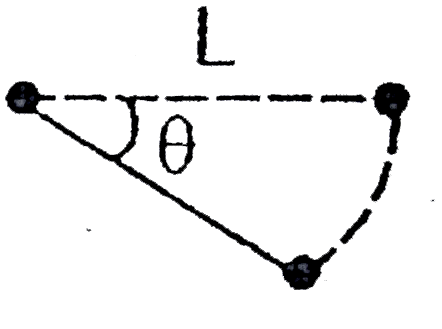
A simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

The times period of swing of simple pendulum is greater than that of rod If L=l
The times period of swing of simple pendulum is equal to that of rod If L=l
The times period of swing of simple pendulum is greater than that of rod If L=2l3
The times period of swing of swing of simle pendulum is equal to that of rod if L=2l3
The correct Answer is:A, D
from conversation of energy
for simple pendulum.
12mL2ω12=mgLsinθ
∴ω1=√2gLsinθ
For homogenous rod
12(ml23)ω22=mg'l2sinθ
ω2=√3glsinθ

when L=23l,ω1=ω2 at all time
so time periods of swinf are equal.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
One end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionA composite rod of mass 2m and length 2l comprises two indentica rods joined end to end at P. The composite rod hinged at one of its ends is kept horizontal as shown in the figure. If it is realeased from rest.
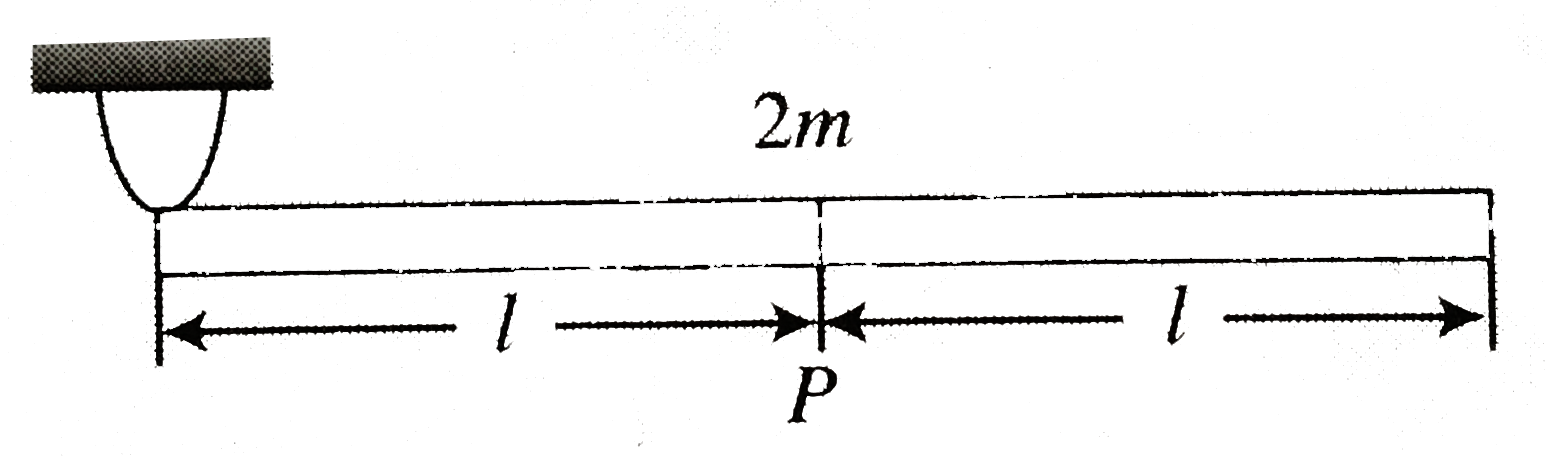
a. find its angular speed when it becomes vertical.
b. If the lower rod gets detached with the upper rod due to centrifugal effect at their joint P, at the vertical position of the composite rod, find their linear and angular velocities just after their separation.
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
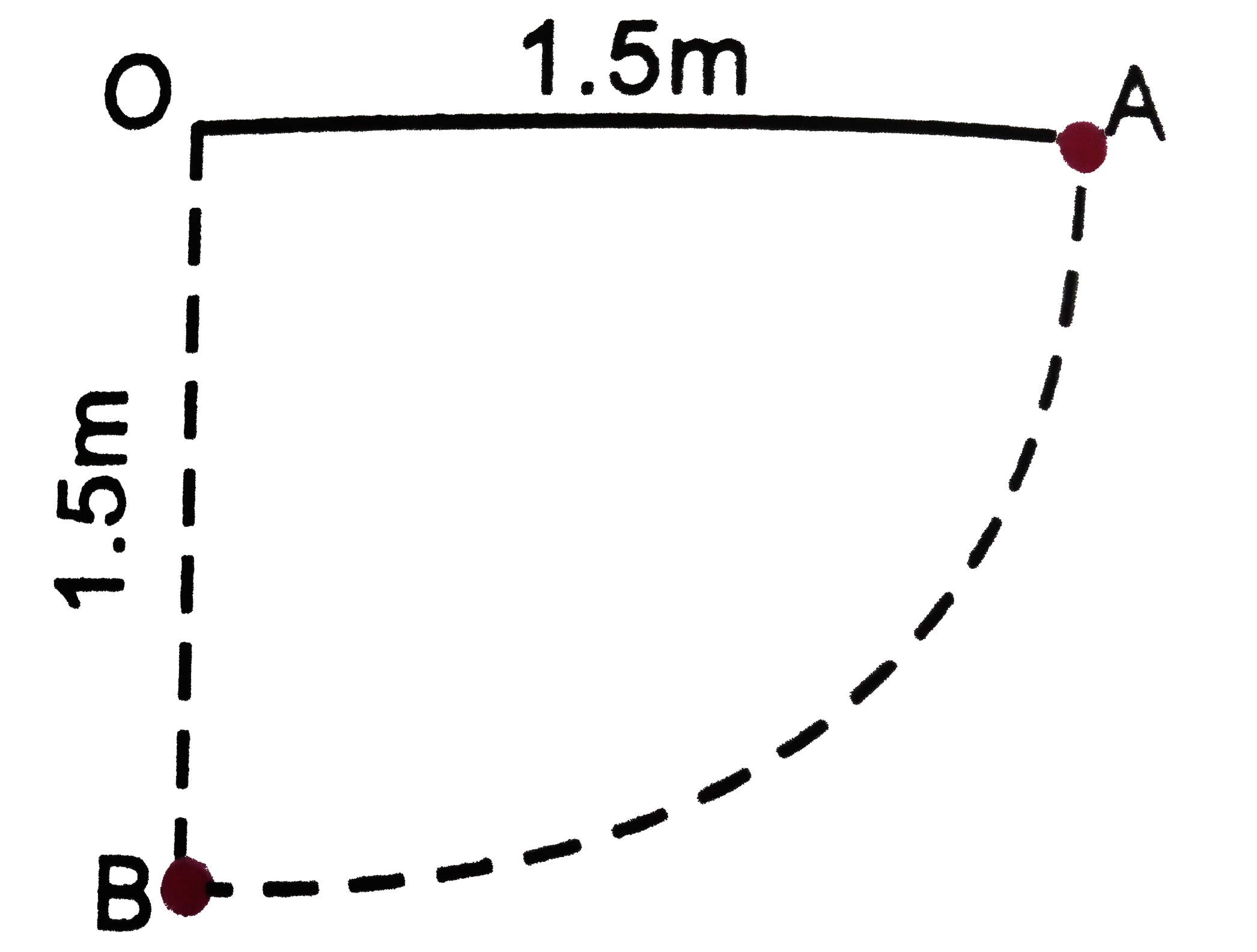
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
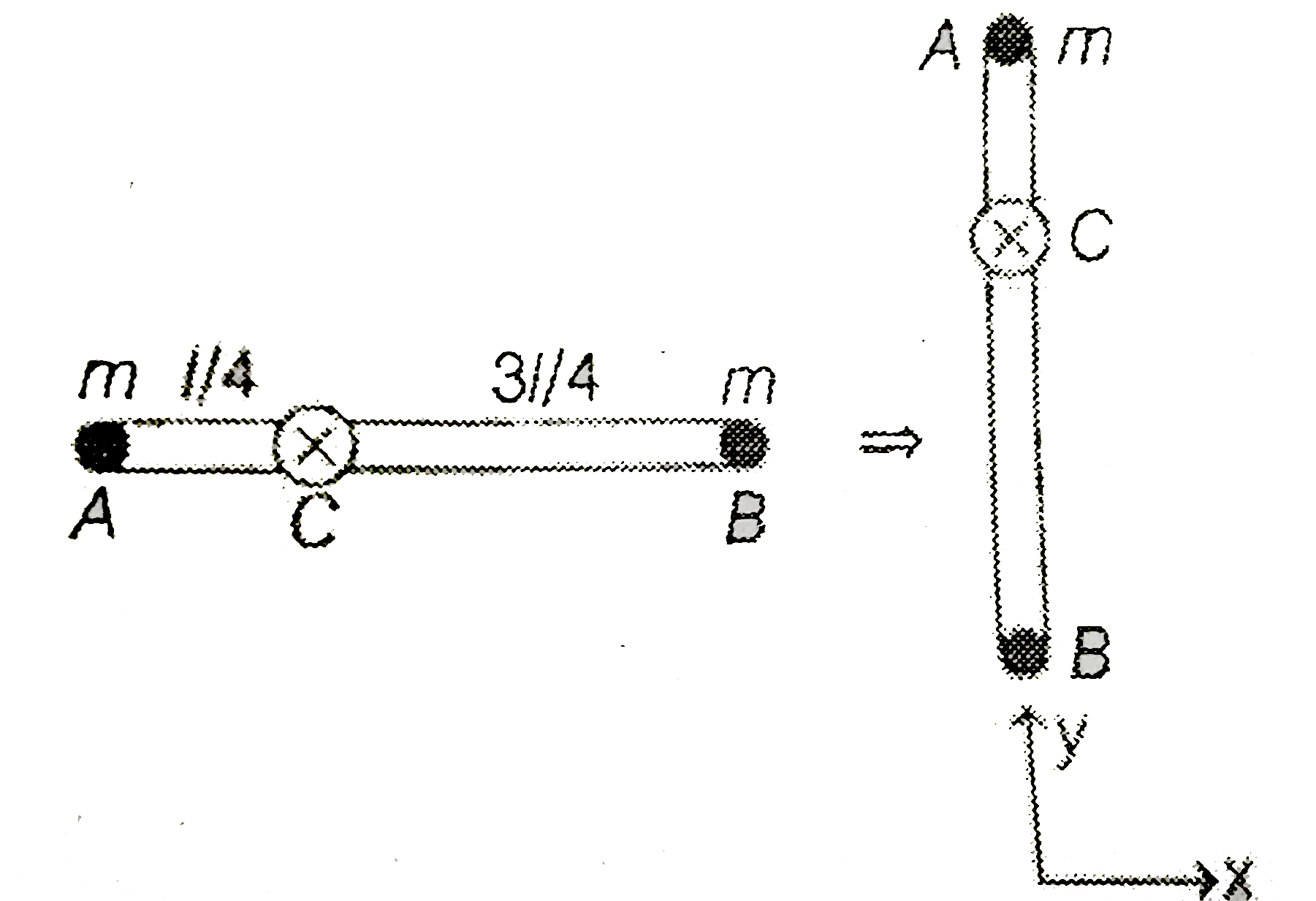
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :
View Solution
