A particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
35 m
15 m
25 m
40 m
The correct Answer is:D
To solve the problem, we will use the equations of motion. The key points are:
1. The particle is thrown vertically upwards.
2. At the maximum height, the final velocity (v) is 0 m/s.
3. The initial velocity (u) at a certain height is given as half of the maximum height.
Let's denote:
- h = maximum height attained by the particle
- h1 = height at which the velocity is 20 m/s
1. Identify the relationship between heights:
Since the velocity at height h1 is given as half of the maximum height, we can write:
h1=h2
2. Use the equation of motion:
We will use the equation of motion:
v2=u2+2as
where:
- v=0 m/s (final velocity at maximum height)
- u=20 m/s (initial velocity at height h1)
- a=−g (acceleration due to gravity, which is negative as it acts downwards)
- s=h1 (the distance traveled to reach maximum height from h1)
Plugging in the values:
0=(20)2+2(−g)(h1)
This simplifies to:
0=400−2gh1
Rearranging gives:
2gh1=400
h1=4002g
3. Substituting the value of g:
Taking g≈10m/s2:
h1=40020=20m
4. Finding the maximum height:
Since h1=h2, we can find h:
h=2h1=2×20=40m
5. Conclusion:
The maximum height attained by the particle is:
h=40m
Final Answer:
The maximum height attained by the particle is 40 meters.
2. At the maximum height, the final velocity (v) is 0 m/s.
3. The initial velocity (u) at a certain height is given as half of the maximum height.
- h = maximum height attained by the particle
- h1 = height at which the velocity is 20 m/s
Since the velocity at height h1 is given as half of the maximum height, we can write:
h1=h2
We will use the equation of motion:
v2=u2+2as
where:
- v=0 m/s (final velocity at maximum height)
- u=20 m/s (initial velocity at height h1)
- a=−g (acceleration due to gravity, which is negative as it acts downwards)
- s=h1 (the distance traveled to reach maximum height from h1)
0=(20)2+2(−g)(h1)
This simplifies to:
0=400−2gh1
Rearranging gives:
2gh1=400
h1=4002g
Taking g≈10m/s2:
h1=40020=20m
Since h1=h2, we can find h:
h=2h1=2×20=40m
The maximum height attained by the particle is:
h=40m
The maximum height attained by the particle is 40 meters.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
58 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View SolutionWhen a particle is thrown vertically upwards, its velocity at one third of its maximum height is 10√2m/s. The maximum height attained by it is
View SolutionA body is projected vertically up with u. Its velocity at half its maximum height is
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionTwo bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
View SolutionA body is thrown vertically upwards with an initial velocity u. Write an expression for the maximum height attained by the body.
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
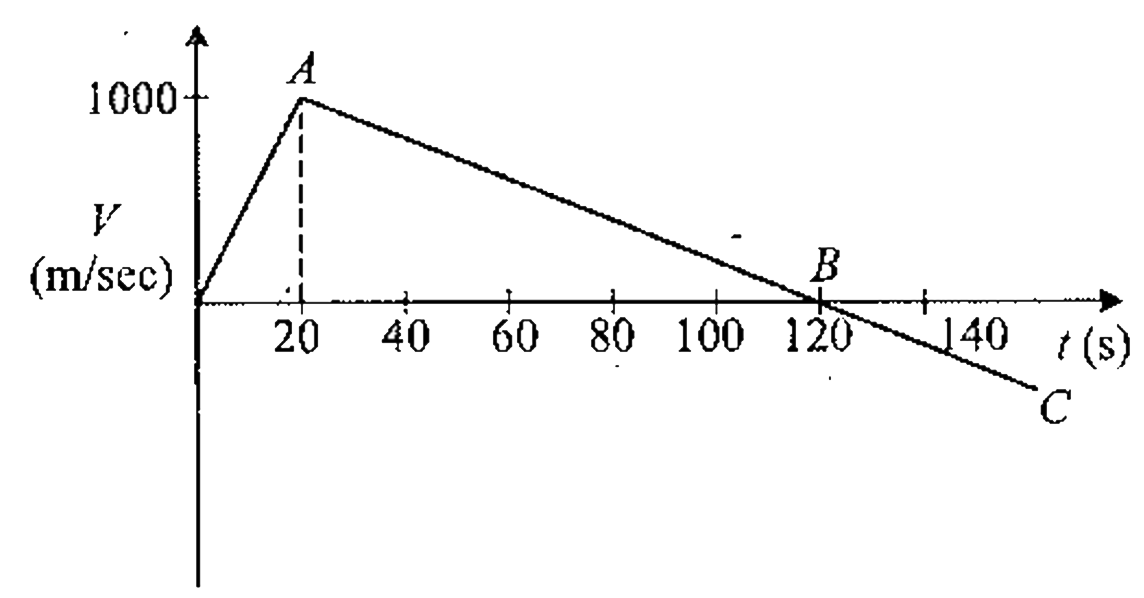
View SolutionA particle is projected vertically upwards from ground with initial velocity u.
a. Find the maximum height H the particle will attain and time T that it will attain and time T that it will take to return to the ground .
 .
.
b. What is the velocity when the particle returns to the ground?
c. What is the displacement and distance travelled by the particle during this time of whole motion.
View Solution
