In a hydraulic lift at a service station, the radii of the large and small piston are in the ratio of 20 : 1. What weight placed on the small piston will be sufficient to lift a car of mass 1200 kg ?
3.75 Kg
37.5 kg
7.5 kg
75 kg
The correct Answer is:A
To solve the problem, we will use the principles of hydraulics, specifically Pascal's law, which states that pressure applied to a confined fluid is transmitted undiminished throughout the fluid.
1. Identify the Given Ratios:
The ratio of the radii of the large piston (R) to the small piston (r) is given as 20:1. This means:
R=20r
2. Calculate the Area Ratio:
The area of a circle is given by A=πR2. Therefore, the areas of the large and small pistons can be expressed as:
Alarge=πR2andAsmall=πr2
The ratio of the areas is:
AlargeAsmall=πR2πr2=R2r2=(Rr)2=(201)2=400:1
3. Apply Pascal's Law:
According to Pascal's law, the pressure exerted on both pistons must be equal:
FlargeAlarge=FsmallAsmall
Where:
- Flarge is the weight of the car (mass m times gravitational acceleration g).
- Fsmall is the weight placed on the small piston.
4. Substituting Values:
The weight of the car is:
Flarge=mcar⋅g=1200kg⋅g
Since we are looking for the weight Fsmall that needs to be placed on the small piston, we can express it as:
Fsmall=msmall⋅g
Thus, we can rewrite the equation:
1200gAlarge=msmallgAsmall
5. Canceling g:
The gravitational acceleration g cancels out from both sides:
1200Alarge=msmallAsmall
6. Using the Area Ratio:
From our earlier calculation, we know:
AlargeAsmall=400
Therefore:
Alarge=400Asmall
Substituting this into the equation gives:
1200400Asmall=msmallAsmall
7. Solving for msmall:
Rearranging gives:
msmall=1200400=3kg
Conclusion:
The weight that needs to be placed on the small piston to lift the car of mass 1200 kg is 3 kg.
The ratio of the radii of the large piston (R) to the small piston (r) is given as 20:1. This means:
R=20r
The area of a circle is given by A=πR2. Therefore, the areas of the large and small pistons can be expressed as:
Alarge=πR2andAsmall=πr2
The ratio of the areas is:
AlargeAsmall=πR2πr2=R2r2=(Rr)2=(201)2=400:1
According to Pascal's law, the pressure exerted on both pistons must be equal:
FlargeAlarge=FsmallAsmall
Where:
- Flarge is the weight of the car (mass m times gravitational acceleration g).
- Fsmall is the weight placed on the small piston.
The weight of the car is:
Flarge=mcar⋅g=1200kg⋅g
Since we are looking for the weight Fsmall that needs to be placed on the small piston, we can express it as:
Fsmall=msmall⋅g
Thus, we can rewrite the equation:
1200gAlarge=msmallgAsmall
The gravitational acceleration g cancels out from both sides:
1200Alarge=msmallAsmall
From our earlier calculation, we know:
AlargeAsmall=400
Therefore:
Alarge=400Asmall
Substituting this into the equation gives:
1200400Asmall=msmallAsmall
Rearranging gives:
msmall=1200400=3kg
The weight that needs to be placed on the small piston to lift the car of mass 1200 kg is 3 kg.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
In a hydraulic lift, used at a service station the radius of the large and small piston are in the ration of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg ?
View SolutionIn a hydraulic machine, the two pistons are of area of cross section in the ratio 1:10. What weight force in needed on the narrow piston to overcome a force of 100 N on the wide piston?
View Solution
Knowledge Check
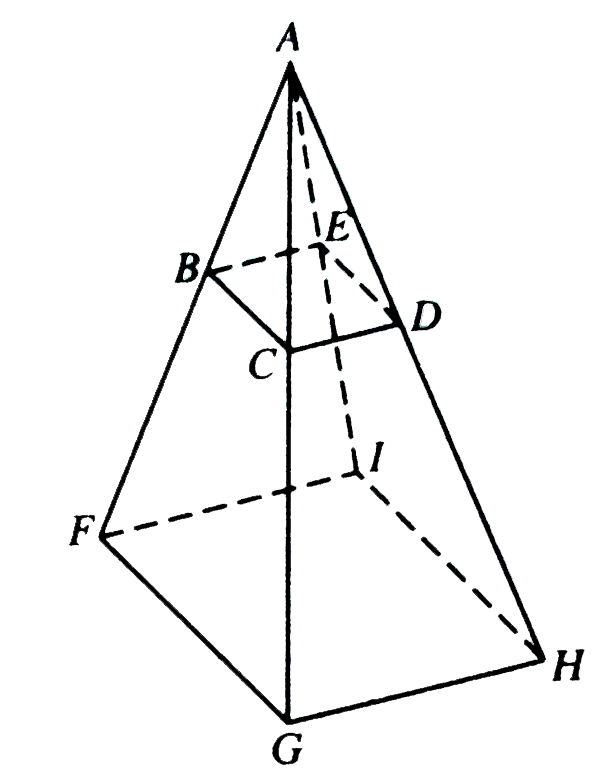
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?A1:2B1:3C1:4D1:8
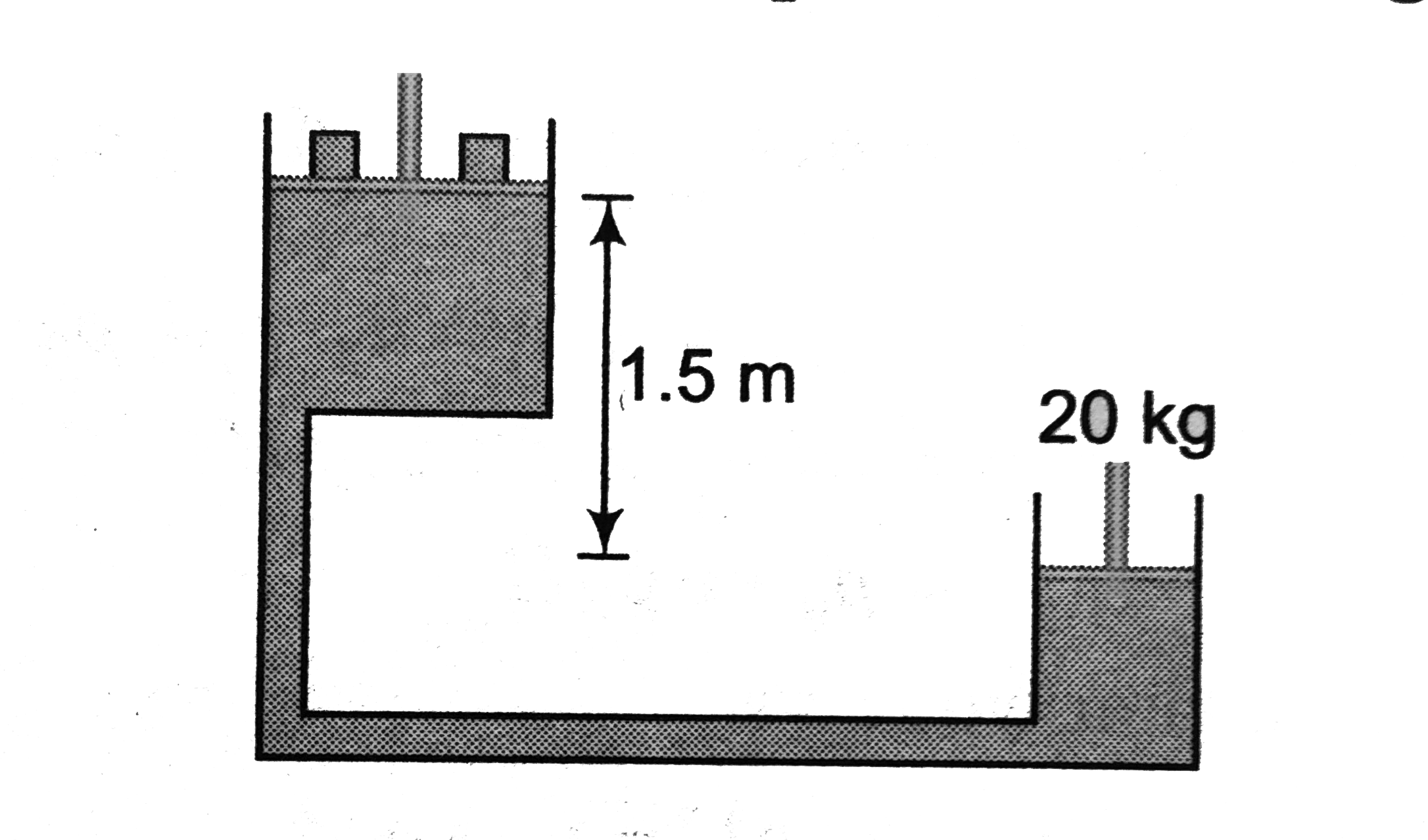
Figure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
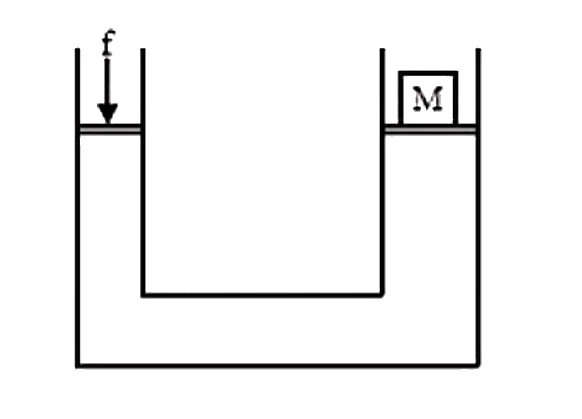
View SolutionIn a hydraulic press, radii of connecting pipes, r1 and r2 are in the ratio 1:2 . In order to lift a heavy mass M on the larger piston, the small piston must be pressed through a minimum force f equal to
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
View SolutionIn an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
View SolutionThe average mass that must be lifted by a hydraulic press is 80kg.If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View Solution
