in a plane progaressive harmonic wave particle speed is always less than the wave speed if.
amplitude of wave is less than
amplitude of wave is greater than
amplitude to wave is less than
amplitude of wave is greater than
The correct Answer is:A
To solve the problem, we need to analyze the relationship between particle speed and wave speed in a plane progressive harmonic wave.
1. Understanding Particle Speed and Wave Speed:
- The particle speed (vp) in a wave is the speed at which a particular point on the wave (a particle) moves up and down as the wave passes.
- The wave speed (v) is the speed at which the wave itself travels through space.
2. Expression for Particle Speed:
- The displacement of a particle in a wave can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
- To find the particle speed, we differentiate the displacement with respect to time:
vp=dxdt=Aωcos(ωt+ϕ)
- The maximum particle speed (vp,max) occurs when cos(ωt+ϕ)=1:
vp,max=Aω
3. Expression for Wave Speed:
- The wave speed is given by:
v=λT
where λ is the wavelength and T is the period of the wave.
- We can express angular frequency ω in terms of T:
ω=2πT
- Thus, the wave speed can also be expressed as:
v=λ⋅2πλ=λT
4. Condition for Particle Speed to be Less than Wave Speed:
- We need to establish the condition under which the maximum particle speed is less than the wave speed:
Aω<v
- Substituting ω and v:
A⋅2πT<λT
- Cancelling T from both sides (assuming T≠0):
A⋅2π<λ
- Rearranging gives:
A<λ2π
5. Conclusion:
- Therefore, the condition for the particle speed to be always less than the wave speed is:
A<λ2π
- This corresponds to option (a) in the question.
Final Answer:
The particle speed is always less than the wave speed if the amplitude A is less than λ2π.
- The particle speed (vp) in a wave is the speed at which a particular point on the wave (a particle) moves up and down as the wave passes.
- The wave speed (v) is the speed at which the wave itself travels through space.
- The displacement of a particle in a wave can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
- To find the particle speed, we differentiate the displacement with respect to time:
vp=dxdt=Aωcos(ωt+ϕ)
- The maximum particle speed (vp,max) occurs when cos(ωt+ϕ)=1:
vp,max=Aω
- The wave speed is given by:
v=λT
where λ is the wavelength and T is the period of the wave.
- We can express angular frequency ω in terms of T:
ω=2πT
- Thus, the wave speed can also be expressed as:
v=λ⋅2πλ=λT
- We need to establish the condition under which the maximum particle speed is less than the wave speed:
Aω<v
- Substituting ω and v:
A⋅2πT<λT
- Cancelling T from both sides (assuming T≠0):
A⋅2π<λ
- Rearranging gives:
A<λ2π
- Therefore, the condition for the particle speed to be always less than the wave speed is:
A<λ2π
- This corresponds to option (a) in the question.
The particle speed is always less than the wave speed if the amplitude A is less than λ2π.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
What is a plane progressive simple harmonic wave ? Establish equation for this wave in two different forms.
View SolutionWhat is a harmonic wave function ?
View SolutionIn sine wave , minimum distance between 2 particles always having same speed is
View SolutionThe equation of a plane progressive wave is y=Asin(πt−x3). Find the value of A for which the wave speed is equal to the maximum particle speed.
View SolutionThe speed of electromagnetic waves depends upon
View SolutionIt has been postulated that there may be some particle moving with speed greater than the speed of light. Such particles have been named as
View SolutionA sine wave is travelling ina medium. The minium distance between the two particles, always having same speed is
View SolutionAssertion: Average speed of a particle in a given time interval is never less than the magnitude of the average velocity.
Reason: The magnitude of the velocity (instantaneous velocity) of a particle is equal to its speed.
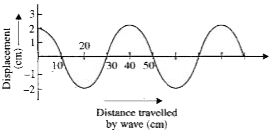
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
View SolutionSpeed of sound waves in air
View Solution
