A person speaking normally produces a sound intensity of 40dB at a distance of 1m. If the threshold intensity for reasonable audibility is 20dB, the maximum distance at which a person can be heard clearly is (2x) meter . Find the value of x.
The correct Answer is:5
To solve the problem, we need to find the maximum distance at which a person can be heard clearly, given the sound intensity levels at different distances. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- The sound intensity level produced by a person speaking normally is 40 dB at a distance of 1 meter.
- The threshold intensity for reasonable audibility is 20 dB.
- We need to find the maximum distance (2x) at which the sound can be heard clearly.
Step 2: Use the Formula for Sound Intensity Level
The sound intensity level in decibels (dB) is given by the formula:
β=10log10(II0)
where:
- β is the sound intensity level in dB,
- I is the sound intensity,
- I0 is the reference intensity, which is 10−12W/m2.
Step 3: Set Up the Equations for the Two Intensity Levels
1. For the first intensity level (40 dB):
40=10log10(I1I0)(Equation 1)
2. For the second intensity level (20 dB):
20=10log10(I2I0)(Equation 2)
Step 4: Solve for Intensities I1 and I2
From Equation 1:
log10(I1I0)=4⟹I1I0=104⟹I1=104I0
From Equation 2:
log10(I2I0)=2⟹I2I0=102⟹I2=102I0
Step 5: Relate the Intensities to Distances
The intensity of sound is inversely proportional to the square of the distance:
I∝1R2
Thus, we can write:
I1I2=R22R21
Substituting the values of I1 and I2:
104I0102I0=R22R21
This simplifies to:
100=R22R21⟹R22=100R21
Taking the square root:
R2=10R1
Step 6: Substitute the Known Distance
Given R1=1m:
R2=10×1=10m
Step 7: Find the Value of x
Since the maximum distance R2 is given as 2x:
2x=10⟹x=102=5m
Final Answer
Thus, the value of x is:
5
- The sound intensity level produced by a person speaking normally is 40 dB at a distance of 1 meter.
- The threshold intensity for reasonable audibility is 20 dB.
- We need to find the maximum distance (2x) at which the sound can be heard clearly.
The sound intensity level in decibels (dB) is given by the formula:
β=10log10(II0)
where:
- β is the sound intensity level in dB,
- I is the sound intensity,
- I0 is the reference intensity, which is 10−12W/m2.
1. For the first intensity level (40 dB):
40=10log10(I1I0)(Equation 1)
2. For the second intensity level (20 dB):
20=10log10(I2I0)(Equation 2)
From Equation 1:
log10(I1I0)=4⟹I1I0=104⟹I1=104I0
log10(I2I0)=2⟹I2I0=102⟹I2=102I0
The intensity of sound is inversely proportional to the square of the distance:
I∝1R2
Thus, we can write:
I1I2=R22R21
Substituting the values of I1 and I2:
104I0102I0=R22R21
This simplifies to:
100=R22R21⟹R22=100R21
Taking the square root:
R2=10R1
Given R1=1m:
R2=10×1=10m
Since the maximum distance R2 is given as 2x:
2x=10⟹x=102=5m
Thus, the value of x is:
5
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A person speaking normally produces a sound intensity of 40dB at a distance of 1m. If the threshold intensity for reasonable audibility is 20dB, the maximum distance at which he can be heard cleary is.
View SolutionA person speaking normally produces a sound intensity of 40dB at a distance of 1m. If the threshold intensity for reasonable audibility is 20dB, the maximum distance at which he can be heard cleary is.
View SolutionAirport authority has made the regulation that maximum allowable intensity level detected by a microphone situated at the end of 1630 m long runway can be 100 dB. An aeroplane when flying at a height of 200 m produces an intensity level of 100 dB on ground. while taking off, this aeroplane makes an angle of 30∘ with horizontal. Find the maximum distance this aeroplane can cover on the runway, so that the regulation are not violated (assume no reflection).
View SolutionAirport authority has made the regulation that maximum allowable intensity level detected by a microphone situated at the end of 1630 m long runway can be 100 dB. An aeroplane when flying at a height of 200 m produces an intensity level of 100 dB on ground. while taking off, this aeroplane makes an angle of 30∘ with horizontal. Find the maximum distance this aeroplane can cover on the runway, so that the regulation are not violated (assume no reflection).
View SolutionThe power of a lens used by short sighted person, is -2D. Find the maximum distance of an object which he can see without spectacles.
View SolutionLoudness of sound from an isotropic point source at a distace of 70cm is 20dB. What is the distance (in m) at which it is not heard.
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
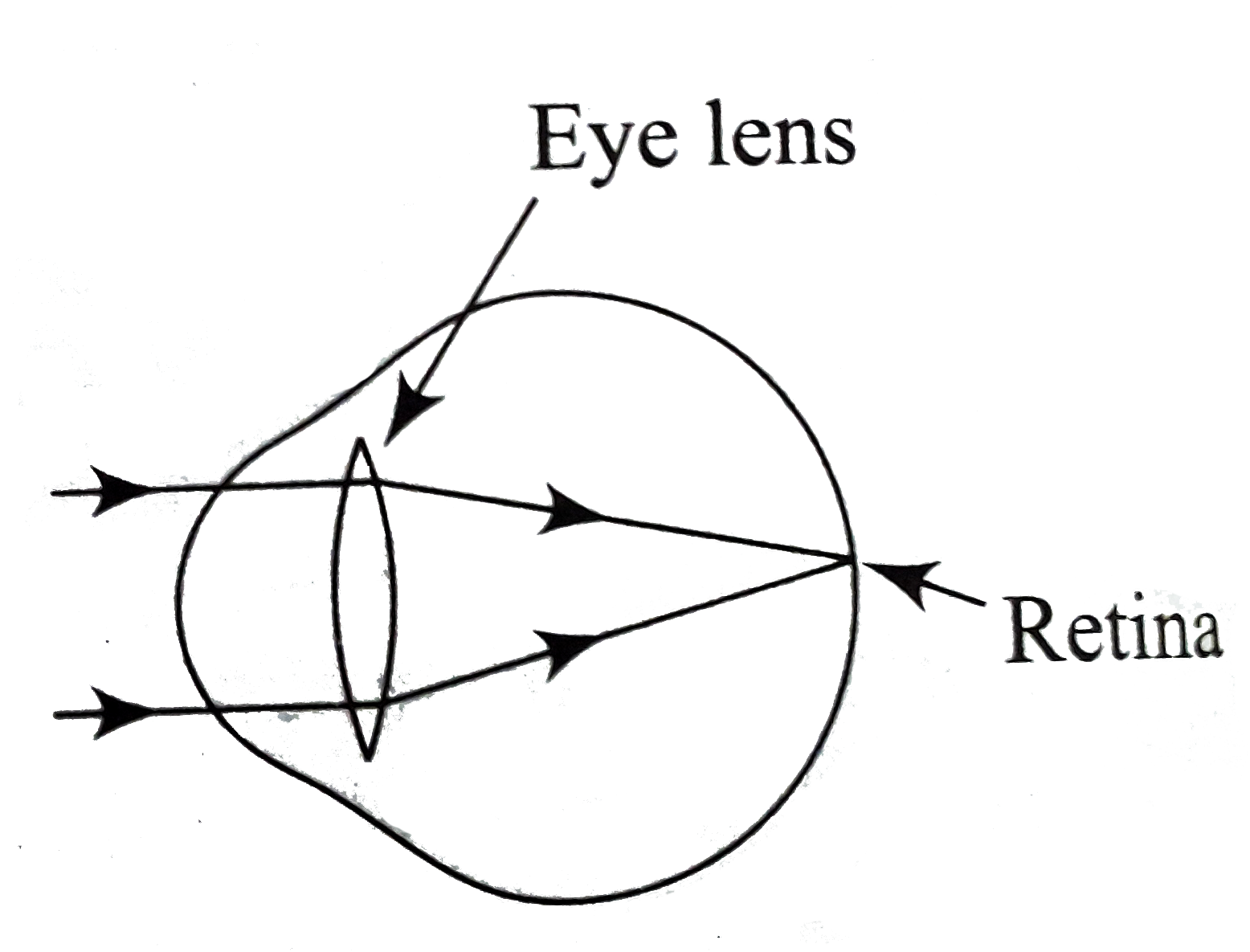
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
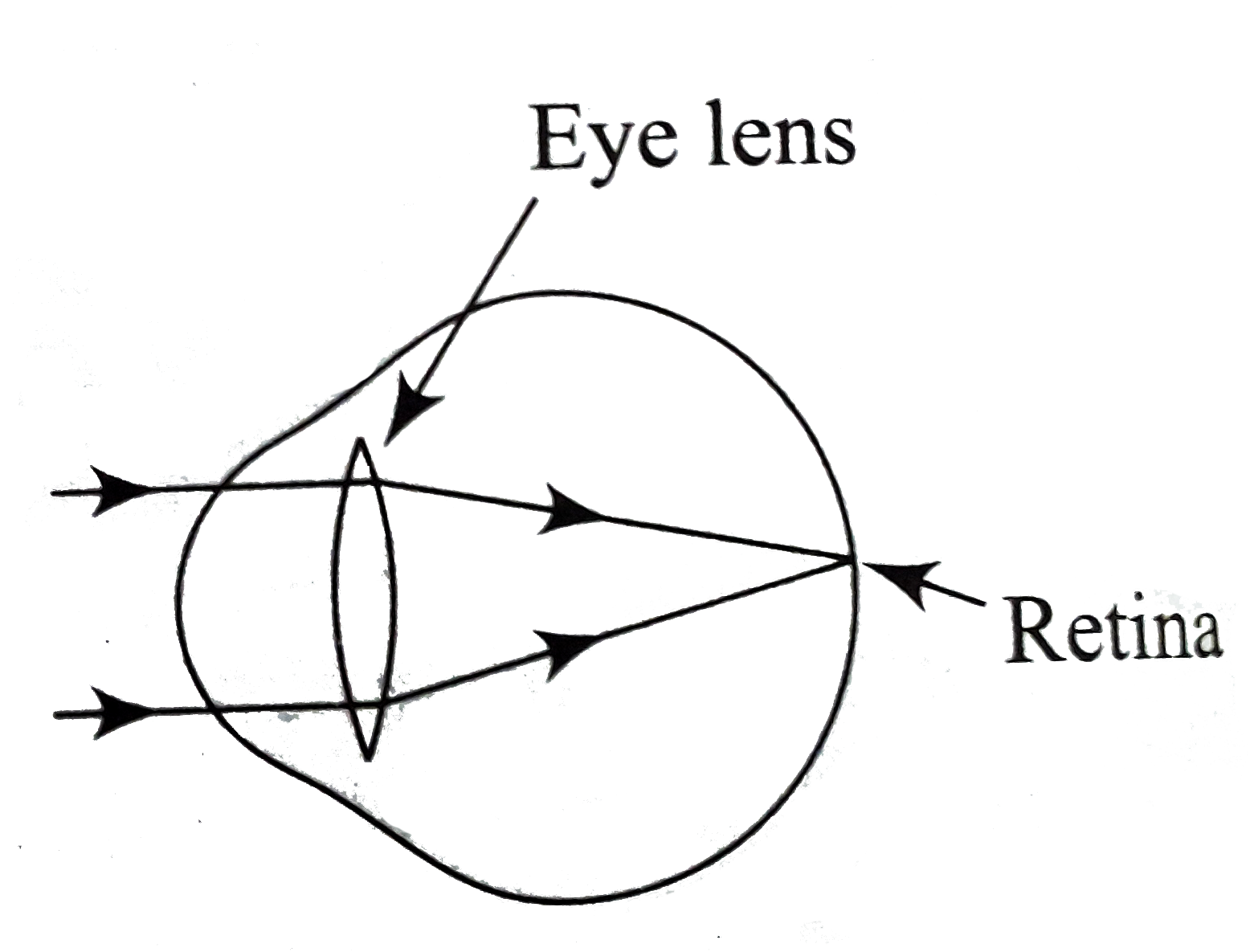
Q. Maximum focal length of a eye lens of a normal person is
View SolutionTwo particles having masses m and 4m are separated by distance l. The distance of the centre of mass from m is x1andx2 is the distance of point at which gravitational field intensity is zero. Find the value of x1x2

View SolutionFind the maximum distance of any normal of the ellipse x2a2+y2b2=1 from its centre,
View Solution
