A string of length 0.4 m and mass 10−2 kg is tightly clamped at its ends. The tension in the string is 1. 6 N. identical wave pulses are produced at one end at equal intervals of time Δt. The value of Δt which allows construction interference between successive pulses is
The correct Answer is:1
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the problem
We have a string of length 0.4 m, mass 10−2 kg, and tension 1.6 N. We need to find the time interval Δt that allows for constructive interference between successive wave pulses produced at one end of the string.
Step 2: Calculate the mass per unit length (μ)
The mass per unit length μ of the string can be calculated using the formula:
μ=masslength=10−2 kg0.4 m=0.025 kg/m
Step 3: Calculate the wave speed (v)
The wave speed v on a string under tension can be calculated using the formula:
v=√Tμ
where T is the tension in the string. Substituting the values:
v=√1.6 N0.025 kg/m=√64=8 m/s
Step 4: Determine the total distance for constructive interference
For constructive interference to occur, the wave must travel to the end of the string and back. Thus, the total distance d traveled by the wave is:
d=2×length=2×0.4 m=0.8 m
Step 5: Calculate the time interval Δt
Using the relationship between speed, distance, and time:
v=dΔt⟹Δt=dv
Substituting the values we found:
Δt=0.8 m8 m/s=0.1 s
Final Answer
Thus, the value of Δt that allows for constructive interference between successive pulses is:
Δt=0.1 seconds
---
We have a string of length 0.4 m, mass 10−2 kg, and tension 1.6 N. We need to find the time interval Δt that allows for constructive interference between successive wave pulses produced at one end of the string.
The mass per unit length μ of the string can be calculated using the formula:
μ=masslength=10−2 kg0.4 m=0.025 kg/m
The wave speed v on a string under tension can be calculated using the formula:
v=√Tμ
where T is the tension in the string. Substituting the values:
v=√1.6 N0.025 kg/m=√64=8 m/s
For constructive interference to occur, the wave must travel to the end of the string and back. Thus, the total distance d traveled by the wave is:
d=2×length=2×0.4 m=0.8 m
Using the relationship between speed, distance, and time:
v=dΔt⟹Δt=dv
Substituting the values we found:
Δt=0.8 m8 m/s=0.1 s
Thus, the value of Δt that allows for constructive interference between successive pulses is:
Δt=0.1 seconds
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A string of length 0.4m and mass 10−2kg is tightly clamped at its ends. The tension in the string is 1.6N. Identical wave pulse are produced at one end at equal intervals of time, Δt. The minimum value of Δt which allows constructive interference of successive pulse is
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View Solution
Knowledge Check
A 1 kg stone at the end of 1 m long string is whirled in a vertical circle at constant speed of 4 m/sec. The tension in the string is 6 N when the stone is at (g=10m/sec2)
Atop of the cirlceBbottom of the circleChalf way downDnone of the above
A string of length 1 m and mass 5 g is fixed at both ends. The tension in the string is 8.0 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string is close to :
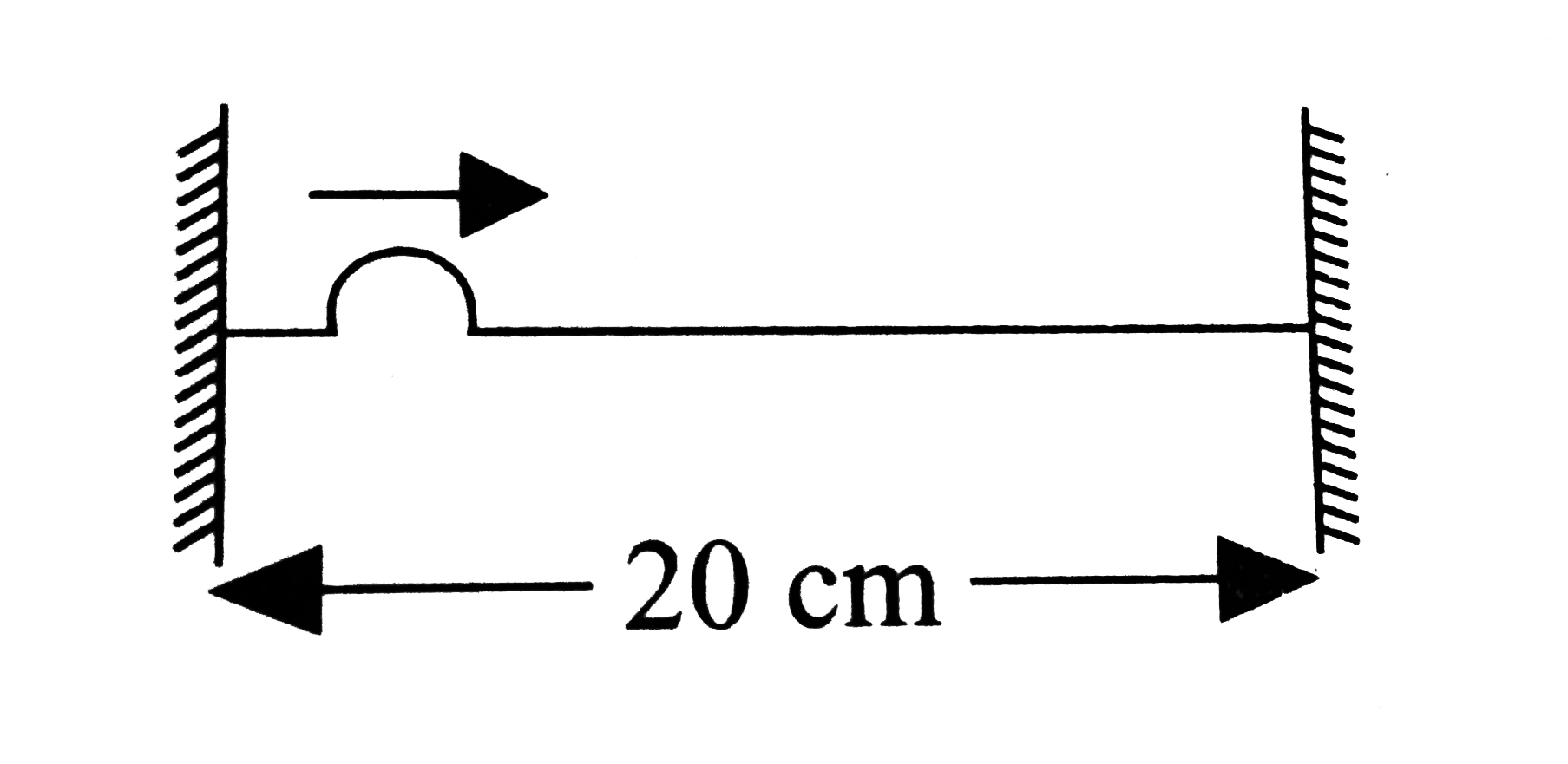
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N.A wave pulse is produced at t=0 nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? (∈×10−2s)
View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).

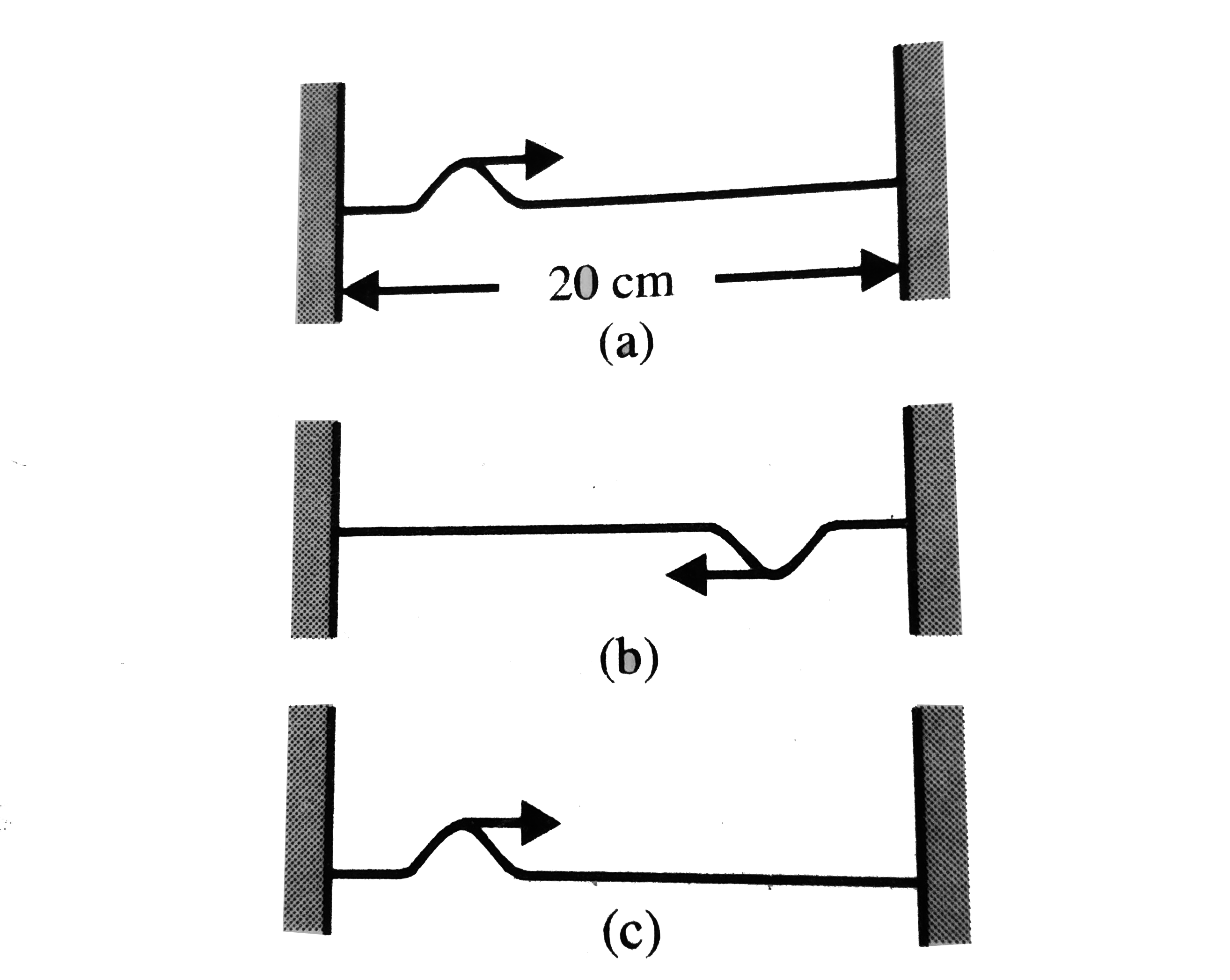
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N . A wave pulse is produced at t=0 near an ends as shown in Fig. 7.17 (b) , which travels towards the other end . When will the string have the shape shown in the Fig . ( c).
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA uniform rope of length 12 m and mass 4 kg is hung vertically from a rigid support transverse wave pulse is produced at lower end. The speed of the wave pulse al x = 2.5 m from lower and will be kg=10 m/s)
View Solution
