Question

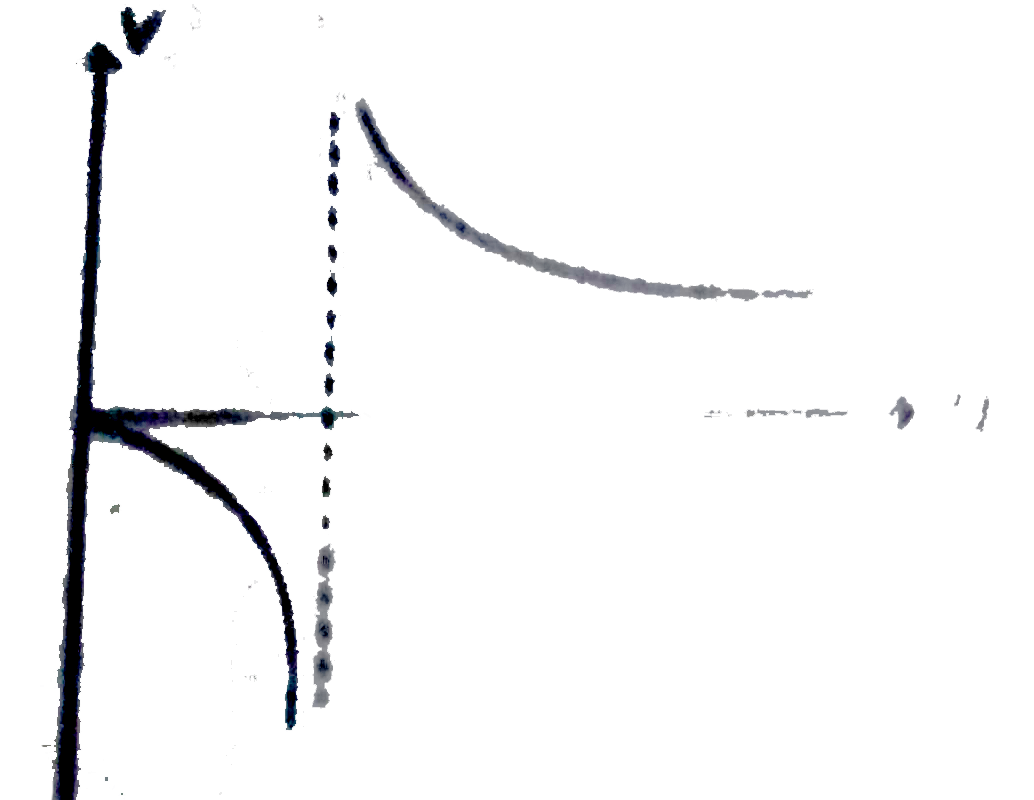
As the position of an object (u) reflected from a concave mirror is varied, the position of the image (v) also varies. By latting the u changes from 0 to $+\infty$ the graph between v versus u will be

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem of finding the relationship between the object distance (u) and the image distance (v) for a concave mirror, we will use the mirror formula and analyze the behavior of the graph as u varies from 0 to +∞.

1. Understand the Mirror Formula:
The mirror formula for a concave mirror is given by:
\( \frac{1}{f} = \frac{1}{v} + \frac{1}{u} \)
Rearranging this gives:
\( \frac{1}{v} = \frac{1}{f} - \frac{1}{u} \)
or equivalently,
\( v = \frac{uf}{u - f} \)

2. Analyze the Behavior as u Approaches 0:
- When \( u = 0 \):
\( v = \frac{0 \cdot f}{0 - f} = 0 \)
- Thus, when the object is at the pole of the mirror, the image is also at the pole.

3. Analyze the Behavior as u Approaches +∞:
- When \( u \) approaches \( +\infty \):
\( v = \frac{u \cdot f}{u - f} \approx f \quad \text{(since } u \text{ is much larger than } f\text{)} \)
- Therefore, as the object moves far away, the image distance approaches the focal length \( f \).

4. Identify Key Points:
- At \( u = 0 \), \( v = 0 \).
- As \( u \to +\infty \), \( v \to f \).

5. Graphing the Relationship:
- The graph starts at the origin (0,0) and approaches the line \( v = f \) as \( u \) increases.
- The curve will be hyperbolic in nature, reflecting that as \( u \) increases, \( v \) approaches a constant value (the focal length).

6. Conclusion:
- The graph of \( v \) versus \( u \) will start from the origin and will asymptotically approach the line \( v = f \) as \( u \) increases.