Same current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
The correct Answer is:A
To find the magnetic field at the point (0, 0, -a) due to three infinitely long wires carrying the same current i along the positive x-, y-, and z-directions, we can follow these steps:
Step 1: Identify the Magnetic Field Contributions
The magnetic field at a point due to a long straight wire carrying current can be calculated using the right-hand rule and the formula:
B=μ0i2πr
where r is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
Step 2: Analyze Each Wire
1. Wire along the x-direction: The wire is at the origin and extends along the x-axis. The point (0, 0, -a) is at a distance r=a from this wire. Using the right-hand rule, the magnetic field Bx at point (0, 0, -a) will be directed in the positive y-direction (j-cap).
Bx=μ0i2πa^j
2. Wire along the y-direction: Similarly, the wire along the y-axis is also at the origin. The point (0, 0, -a) is at a distance r=a from this wire. Using the right-hand rule, the magnetic field By at point (0, 0, -a) will be directed in the negative x-direction (-i-cap).
By=−μ0i2πa^i
3. Wire along the z-direction: The magnetic field at the point (0, 0, -a) due to the wire along the z-direction is zero because the point lies directly on the wire itself.
Bz=0
Step 3: Calculate the Net Magnetic Field
The net magnetic field Bnet at the point (0, 0, -a) is the vector sum of the contributions from the three wires:
Bnet=Bx+By+Bz
Substituting the values we found:
Bnet=μ0i2πa^j−μ0i2πa^i+0
Thus,
Bnet=μ0i2πa^j−μ0i2πa^i
Final Answer
The magnetic field at the point (0, 0, -a) is:
Bnet=μ0i2πa^j−μ0i2πa^i
The magnetic field at a point due to a long straight wire carrying current can be calculated using the right-hand rule and the formula:
B=μ0i2πr
where r is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
1. Wire along the x-direction: The wire is at the origin and extends along the x-axis. The point (0, 0, -a) is at a distance r=a from this wire. Using the right-hand rule, the magnetic field Bx at point (0, 0, -a) will be directed in the positive y-direction (j-cap).
Bx=μ0i2πa^j
By=−μ0i2πa^i
Bz=0
The net magnetic field Bnet at the point (0, 0, -a) is the vector sum of the contributions from the three wires:
Bnet=Bx+By+Bz
Substituting the values we found:
Bnet=μ0i2πa^j−μ0i2πa^i+0
Thus,
Bnet=μ0i2πa^j−μ0i2πa^i
The magnetic field at the point (0, 0, -a) is:
Bnet=μ0i2πa^j−μ0i2πa^i
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:More than One Option is Correct
Explore 25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Comprehension type Questions
Explore 16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Integer type Questions
Explore 10 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
Similar Questions
Equal currents are flowing in three infinitely long wires along positive x,y and z -directions. The magnetic field at a point (0,0−a) would be (i=current in each wire)
View SolutionA current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionAn electric current I flows through an infinitely long conductor as shown in Figure 2(a) below. Write an expression and direction for the magnetic field at point P.

View SolutionFind the electric field vector at P (a,a,a) due to three infinitely long lines of charges along the x-, y- and z-axis, respectively. The charge density i.e. charge per unit length of each wire is (λ),
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point P is
 .
.
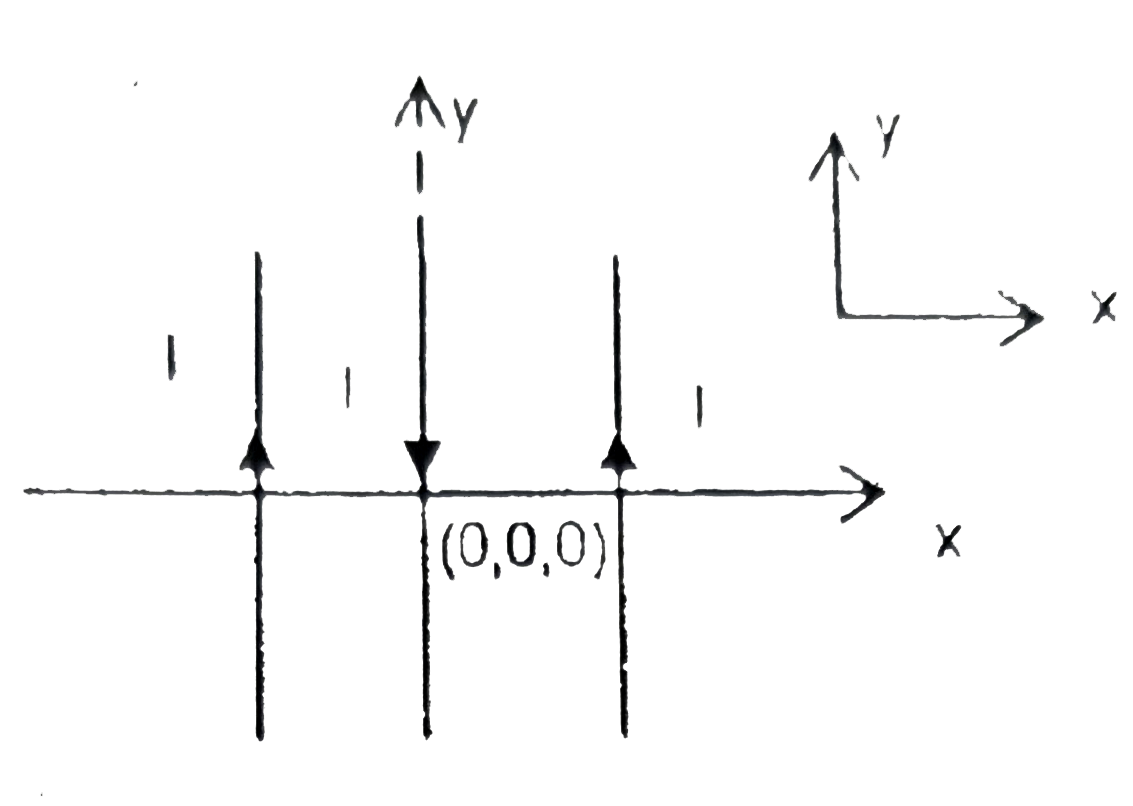
View SolutionThe location of three long wires carrying same current I are x=−a, x=0 and x=+ a respectively as shown in figure. The magnetic field at point (0, 0, a) is
View SolutionA current I ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is .
View SolutionTwo parallel, long wires carry current i1 and i2 withi1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 30μT. If the direction of i1 is reversed , the field becomes 90μT. The ratio i1/i2 is
View Solution
