A car is moving rectilinearly on a horizontal path with acceleration a0.A person sitting inside the car observes that an insect S is crawling up the screen with an acceleration a.If θ is the inclination of the wind screen with the horizontal, then the acceleration of the insect.
parallel to screen is a+a0cosθ
along the horizontal is a0−acosθ
perpendicular to screen is a0sinθ
perpendicular to screen is a0tanθ
The correct Answer is:B, C
To solve the problem, we need to analyze the motion of the insect as observed from the car. We will break down the accelerations into components based on the inclination of the windscreen.
1. Identify the Given Information:
- The car is moving with an acceleration a0.
- The insect is crawling up the screen with an acceleration a.
- The angle of inclination of the windscreen with the horizontal is θ.
2. Draw a Diagram:
- Visualize the car moving horizontally and the windscreen inclined at an angle θ.
- Mark the direction of the car's acceleration a0 and the insect's acceleration a.
3. Resolve the Accelerations:
- The acceleration of the car a0 can be resolved into two components:
- Horizontal Component: a0cosθ
- Vertical Component: a0sinθ
- The acceleration of the insect a can also be resolved into components:
- Horizontal Component: acosθ
- Vertical Component: asinθ
4. Set Up the Equations:
- Since the observer inside the car sees the insect moving, we can set up the following equations based on the components:
- Horizontal Direction: The net acceleration in the horizontal direction as observed from the car is:
ahorizontal=a0−acosθ
- Vertical Direction: The net acceleration in the vertical direction is:
avertical=a−a0sinθ
5. Determine the Resultant Acceleration:
- The resultant acceleration of the insect as observed from the car can be calculated using the Pythagorean theorem:
ainsect=√(a0−acosθ)2+(a−a0sinθ)2
6. Conclusion:
- The acceleration of the insect as observed by the person in the car is given by the resultant of the horizontal and vertical components derived above.
- The car is moving with an acceleration a0.
- The insect is crawling up the screen with an acceleration a.
- The angle of inclination of the windscreen with the horizontal is θ.
- Visualize the car moving horizontally and the windscreen inclined at an angle θ.
- Mark the direction of the car's acceleration a0 and the insect's acceleration a.
- The acceleration of the car a0 can be resolved into two components:
- Horizontal Component: a0cosθ
- Vertical Component: a0sinθ
- The acceleration of the insect a can also be resolved into components:
- Horizontal Component: acosθ
- Vertical Component: asinθ
- Since the observer inside the car sees the insect moving, we can set up the following equations based on the components:
- Horizontal Direction: The net acceleration in the horizontal direction as observed from the car is:
ahorizontal=a0−acosθ
- Vertical Direction: The net acceleration in the vertical direction is:
avertical=a−a0sinθ
- The resultant acceleration of the insect as observed from the car can be calculated using the Pythagorean theorem:
ainsect=√(a0−acosθ)2+(a−a0sinθ)2
- The acceleration of the insect as observed by the person in the car is given by the resultant of the horizontal and vertical components derived above.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A bob is hanging over a pulley inside a car through a string. The second end of the string is in the hands of a person standing in the car. The car is moving with constant acceleration a directed horizontally as shown in fig. The other end of the string is pulled with constant acceleration a vertically. The tension in the string is equal to

View SolutionA car is moving on a horizontal road with constant acceleration 'a' . A bob of mass 'm' is suspended from the ceiling of car. The mean position about which the bob will oscillate is given by ('θ' is angle with vertical)
View Solution
Knowledge Check
A train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60(∘) to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
A3 m s−2B5 m s−2C8 m s−2D6 m s−2
A large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle θ with horizontal from box frame. For the given u, the value of θ for which horizontal range inside he box will be maximum is

View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
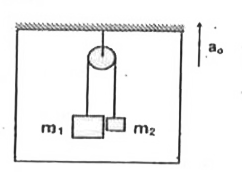
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
View SolutionA train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60∘ to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionA bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays t rest with respect to the car when the string is making an angle θ with the vertical.The linear momentum of the bob as seen from the road is increasing with momentum? If not, where is the external force which changes the linear momentum?
View SolutionA block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9m,μ=0.5 and g=10ms−2
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA car is moving on a plane inclined at 30∘ to the horizontal with an acceleration of 10m/s2 parallel to the plane upward. A bob is suspended by a string from the roof. The angle in degrees which the string makes with the vertical is: (Assume that the bob does not move relative to car) [g=10m/s2]
View Solution
