Rate of dissipation of Joule's heat in resistance per unit volume is (symbols have usual meaning)
None of these
The correct Answer is:C
To find the rate of dissipation of Joule's heat in resistance per unit volume, we can follow these steps:
Step 1: Understand Joule's Law
Joule's law states that the power (P) dissipated as heat in a resistor is given by the formula:
P=V⋅I
where V is the voltage across the resistor and I is the current flowing through it.
Hint: Remember that power is the rate at which energy is dissipated.
Step 2: Relate Voltage and Current to Electric Field and Current Density
We can express voltage (V) in terms of electric field (E) and length (L) of the conductor:
V=E⋅L
Similarly, current (I) can be expressed in terms of current density (J) and cross-sectional area (A):
I=J⋅A
Hint: Think about how electric field and current density relate to the physical dimensions of the conductor.
Step 3: Substitute the Expressions into the Power Formula
Substituting the expressions for voltage and current into the power formula gives:
P=(E⋅L)⋅(J⋅A)
Hint: Keep track of the units and dimensions as you substitute.
Step 4: Simplify the Expression
Now, we can simplify this expression:
P=E⋅J⋅(L⋅A)
Since L⋅A is the volume (V) of the conductor, we can rewrite the equation as:
P=E⋅J⋅V
Hint: Remember that volume is the product of length and area.
Step 5: Find the Rate of Dissipation of Joule's Heat per Unit Volume
To find the rate of dissipation of Joule's heat per unit volume, we divide the power by the volume:
Rate of dissipation per unit volume=PV=E⋅J⋅VV=E⋅J
Hint: Dividing by volume helps us find the rate per unit volume.
Final Answer
Thus, the rate of dissipation of Joule's heat in resistance per unit volume is:
E⋅J
Joule's law states that the power (P) dissipated as heat in a resistor is given by the formula:
P=V⋅I
where V is the voltage across the resistor and I is the current flowing through it.
We can express voltage (V) in terms of electric field (E) and length (L) of the conductor:
V=E⋅L
Similarly, current (I) can be expressed in terms of current density (J) and cross-sectional area (A):
I=J⋅A
Substituting the expressions for voltage and current into the power formula gives:
P=(E⋅L)⋅(J⋅A)
Now, we can simplify this expression:
P=E⋅J⋅(L⋅A)
Since L⋅A is the volume (V) of the conductor, we can rewrite the equation as:
P=E⋅J⋅V
To find the rate of dissipation of Joule's heat per unit volume, we divide the power by the volume:
Rate of dissipation per unit volume=PV=E⋅J⋅VV=E⋅J
Thus, the rate of dissipation of Joule's heat in resistance per unit volume is:
E⋅J
Topper's Solved these Questions
Similar Questions
KE per unit volume is:
View SolutionName
Mass per unit volume
View SolutionBohr magnetonis given by (symbols have their usual meanings)
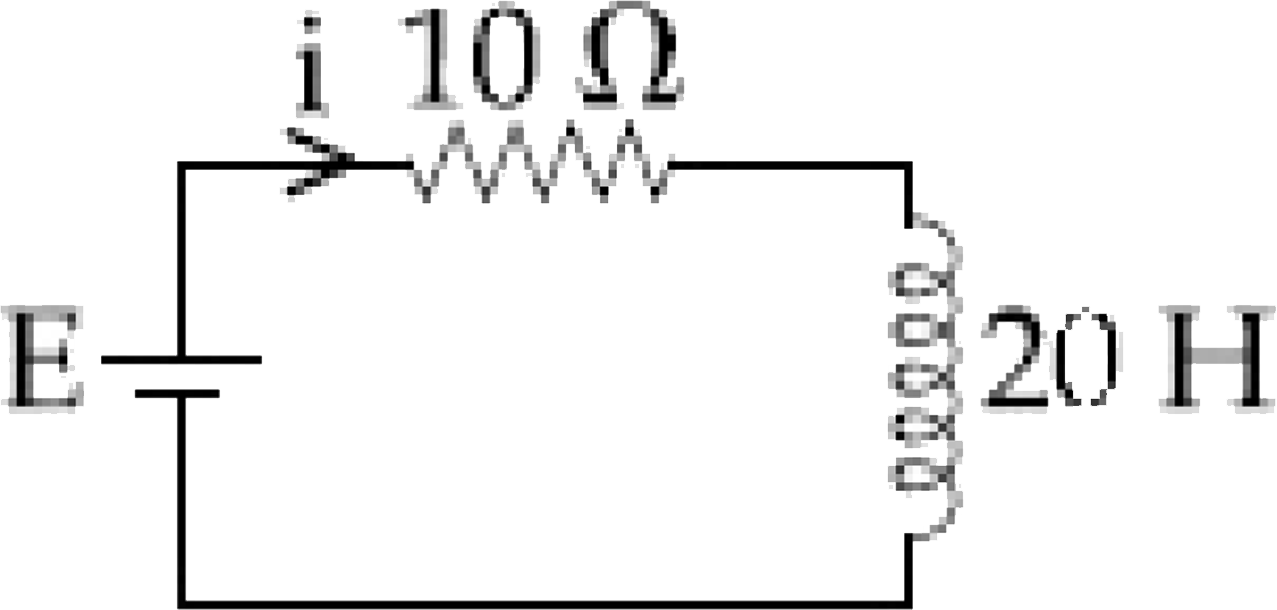
View SolutionA 20 Henry inductor coil is connected to a 10ohm resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
View Solutionthe correct form of Strokes law is (symbols have their usual meanings)
View SolutionEnergy per unit volume represents
View SolutionDisplacement current can be expressed as (symbols have their usual meanings)
View SolutionAverage energy loss due to inductance (L) of circuit is (symbols have their usual meaning)
View SolutionWhich of the following is correct expression for the stopping distance of a vechicle? (symbols have their usual meaning)
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View Solution
