A 20 Henry inductor coil is connected to a 10ohm resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
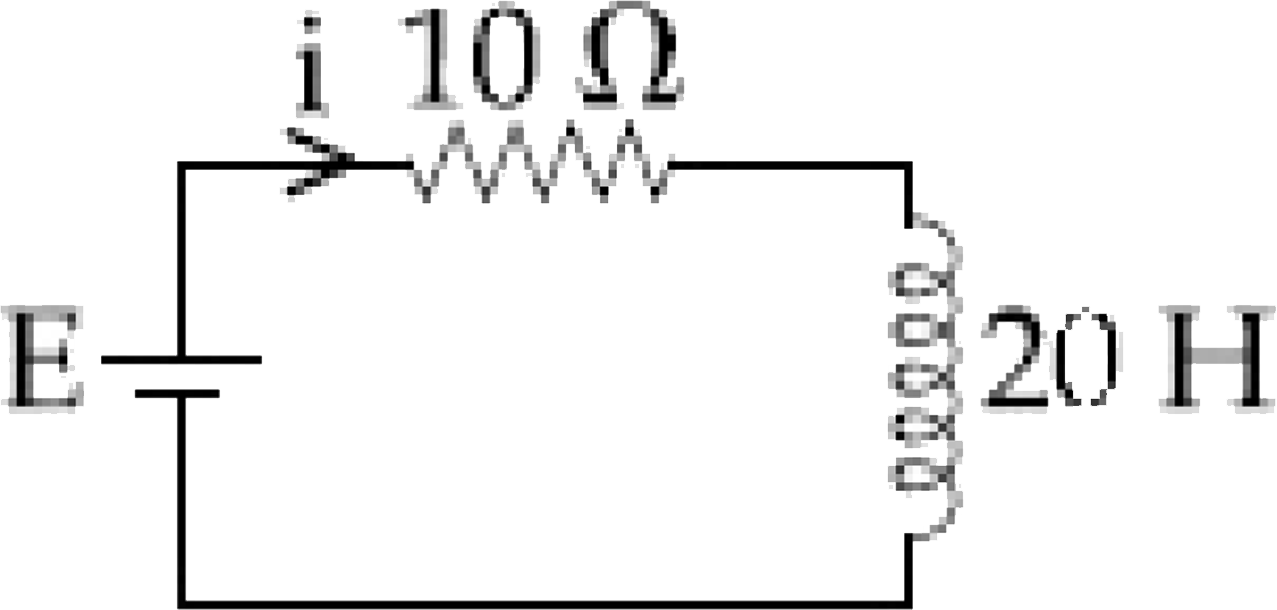
21ln2
12ln2
2ln2
ln2
The correct Answer is:B
Step by step video & image solution for A 20 Henry inductor coil is connected to a 10ohm resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a series lags the applied emf. The rate at which energy is dissipated in the resistor, can be increased by
View SolutionAn inductor coil is connected to an source through a 60Ω resistance in series. The source voltage, voltage across the coil and voltage across the resistance are found to be 33V, 27V and 12V respectively. The resistance of the coil is
A. 30Ω
B. 45Ω
C. 105Ω
D. 75Ω
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
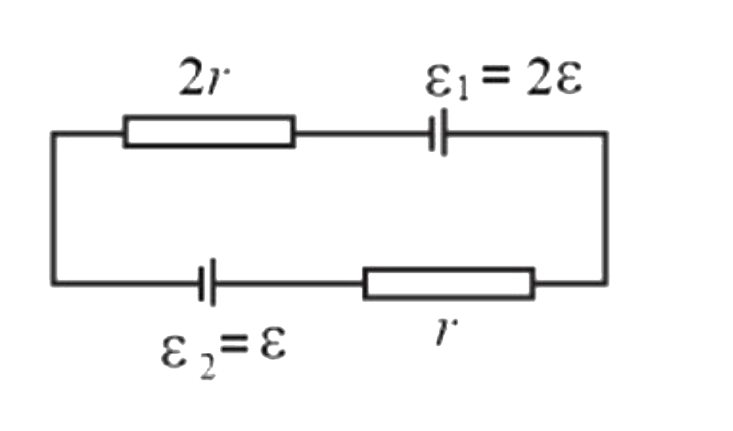
View SolutionIn the circuit shown if the internal resistance of each cell is r, then the rate at which the chemical energy of ε1 is being consumed is
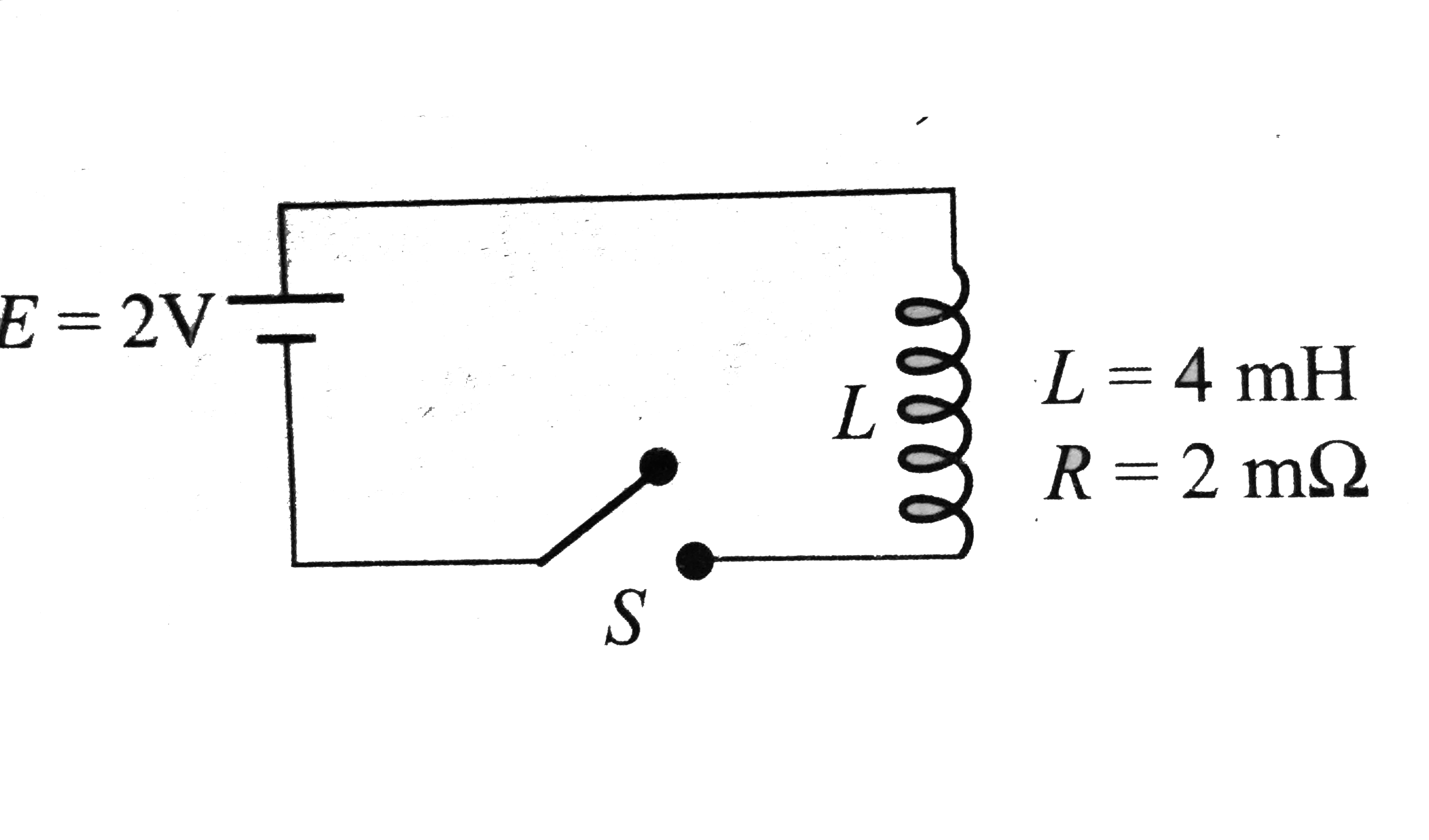
View SolutionThe cell in the circuit shows in Fig is ideal. The coil has an inductance of 4mH and a resistance of 2mΩ. The switch is closed at t=0. The amount of energy stored in the inductor at t=2s is (take e=3)
View SolutionThe circuit shown in fig. Is in steady state.

i. Find the energy stored in the capacitors shown in fig.
ii. Find the rate at which battery supplies energy.
View Solution
