A container X has volume double that of container Y and both are connected by a thin tube. Both contains same ideal gas. The temperature os X is 200K and that of Y is 400K. If mass of gas in X is m then in Y it will be.
m/8
m/6
m/4
m/2
The correct Answer is:C
To solve the problem, we will use the ideal gas law and the relationship between pressure, volume, and temperature for the two containers.
1. Identify the Given Information:
- Volume of container X (Vx) = 2 * Volume of container Y (Vy)
- Temperature of container X (Tx) = 200 K
- Temperature of container Y (Ty) = 400 K
- Mass of gas in container X (Mx) = m
- We need to find the mass of gas in container Y (My).
2. Use the Ideal Gas Law:
The pressure in both containers is the same since they are connected by a thin tube. The ideal gas law can be expressed as:
P=nRTV
Where:
- P = Pressure
- n = Number of moles
- R = Universal gas constant
- T = Temperature
- V = Volume
3. Set Up the Pressure Equations:
For container X:
Px=nxRTxVx
For container Y:
Py=nyRTyVy
Since Px=Py, we can equate these two equations:
nxRTxVx=nyRTyVy
4. Cancel R from Both Sides:
nxTxVx=nyTyVy
5. Substitute Known Values:
Substitute Vx=2Vy:
nxTx2Vy=nyTyVy
Now, we can cancel Vy from both sides:
nxTx2=nyTy
6. Express Number of Moles in Terms of Mass:
The number of moles n can be expressed as:
nx=MxMmandny=MyMm
where Mm is the molar mass (constant for both gases since they are the same).
7. Substituting Moles into the Equation:
Substitute nx and ny into the equation:
MxMm⋅Tx/2=MyMm⋅Ty
Cancel Mm:
MxTx2=MyTy
8. Rearranging to Find Mass in Container Y:
My=MxTx2Ty
9. Substituting the Known Values:
Substitute Mx=m, Tx=200K, and Ty=400K:
My=m⋅2002⋅400
Simplifying this gives:
My=m⋅200800=m4
Final Answer:
The mass of gas in container Y is My=m4.
- Volume of container X (Vx) = 2 * Volume of container Y (Vy)
- Temperature of container X (Tx) = 200 K
- Temperature of container Y (Ty) = 400 K
- Mass of gas in container X (Mx) = m
- We need to find the mass of gas in container Y (My).
The pressure in both containers is the same since they are connected by a thin tube. The ideal gas law can be expressed as:
P=nRTV
Where:
- P = Pressure
- n = Number of moles
- R = Universal gas constant
- T = Temperature
- V = Volume
For container X:
Px=nxRTxVx
For container Y:
Py=nyRTyVy
Since Px=Py, we can equate these two equations:
nxRTxVx=nyRTyVy
nxTxVx=nyTyVy
Substitute Vx=2Vy:
nxTx2Vy=nyTyVy
Now, we can cancel Vy from both sides:
nxTx2=nyTy
The number of moles n can be expressed as:
nx=MxMmandny=MyMm
where Mm is the molar mass (constant for both gases since they are the same).
Substitute nx and ny into the equation:
MxMm⋅Tx/2=MyMm⋅Ty
Cancel Mm:
MxTx2=MyTy
My=MxTx2Ty
Substitute Mx=m, Tx=200K, and Ty=400K:
My=m⋅2002⋅400
Simplifying this gives:
My=m⋅200800=m4
The mass of gas in container Y is My=m4.
Topper's Solved these Questions
Similar Questions
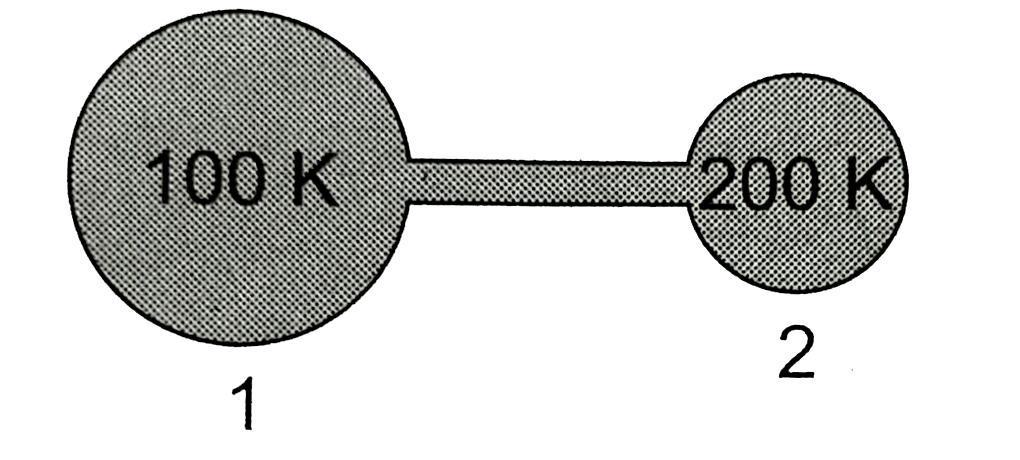
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature 100K and 200K respectively. If the mass of the gas in 1 be m then what is the mass of the gas in flask 2
View SolutionIn two containers X and Y same gas is filled. If the pressure, volume and absolute temperature of gas in X are three times as compared to that in Y and if the mass of X is mg, the mass of Y is
View SolutionFind the average momentum of molecules of hydrogen gas in a container at temperature 300K.
View SolutionFind the average momentum of molecules of hydrogen gas in a container at temperature 300K.
View SolutionIf both the temperature and the volume of an ideal gas are doubled, the pressure
View SolutionSome gas at 300K is enclosed in a container. Now the container is placed on a fast moving train. While the train is in motion, the temperature of the gas
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionVessel A contains an ideal gas at a pressure 5×105 Pa and is connected with a heat source which maintains its temperature at 300K. Another vessel B which has four time greater inner volume contains the same gas at a pressure 105 Pa and is connected to a heat source which maintains its temperature at 400K. What will be the pressure of entire system if two vessels are connected by a narrow tube tap:-
View SolutionA monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature t0 and pressure P0 . Find the pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View Solution
