Two bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
m1m2
√m2m1
√m1m2
m21m22
The correct Answer is:C
To solve the problem, we need to analyze the relationship between kinetic energy and momentum for two bodies with masses m1 and m2 that have equal kinetic energies.
1. Understanding Kinetic Energy:
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass and v is the velocity of the object.
2. Setting Up the Equation for Equal Kinetic Energies:
Since both bodies have equal kinetic energies, we can write:
KE1=KE2
This gives us:
12m1v21=12m2v22
Simplifying this, we get:
m1v21=m2v22
3. Expressing Momentum:
The momentum p of an object is given by:
p=mv
Therefore, for the two bodies, we have:
p1=m1v1andp2=m2v2
4. Relating Momentum to Kinetic Energy:
From the kinetic energy equation, we can express v1 and v2 in terms of kinetic energy KE:
v1=√2KEm1andv2=√2KEm2
5. Substituting for Momentum:
Now substituting v1 and v2 into the momentum equations:
p1=m1√2KEm1=√2m1KE
p2=m2√2KEm2=√2m2KE
6. Finding the Ratio of Momenta:
Now, we can find the ratio of the momenta:
p1p2=√2m1KE√2m2KE=√m1√m2=√m1m2
7. Conclusion:
Therefore, the ratio of the momenta p1p2 is equal to:
p1p2=√m1m2
Final Answer:
p1p2=√m1m2
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass and v is the velocity of the object.
Since both bodies have equal kinetic energies, we can write:
KE1=KE2
This gives us:
12m1v21=12m2v22
Simplifying this, we get:
m1v21=m2v22
The momentum p of an object is given by:
p=mv
Therefore, for the two bodies, we have:
p1=m1v1andp2=m2v2
From the kinetic energy equation, we can express v1 and v2 in terms of kinetic energy KE:
v1=√2KEm1andv2=√2KEm2
Now substituting v1 and v2 into the momentum equations:
p1=m1√2KEm1=√2m1KE
p2=m2√2KEm2=√2m2KE
Now, we can find the ratio of the momenta:
p1p2=√2m1KE√2m2KE=√m1√m2=√m1m2
Therefore, the ratio of the momenta p1p2 is equal to:
p1p2=√m1m2
p1p2=√m1m2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Two bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View Solution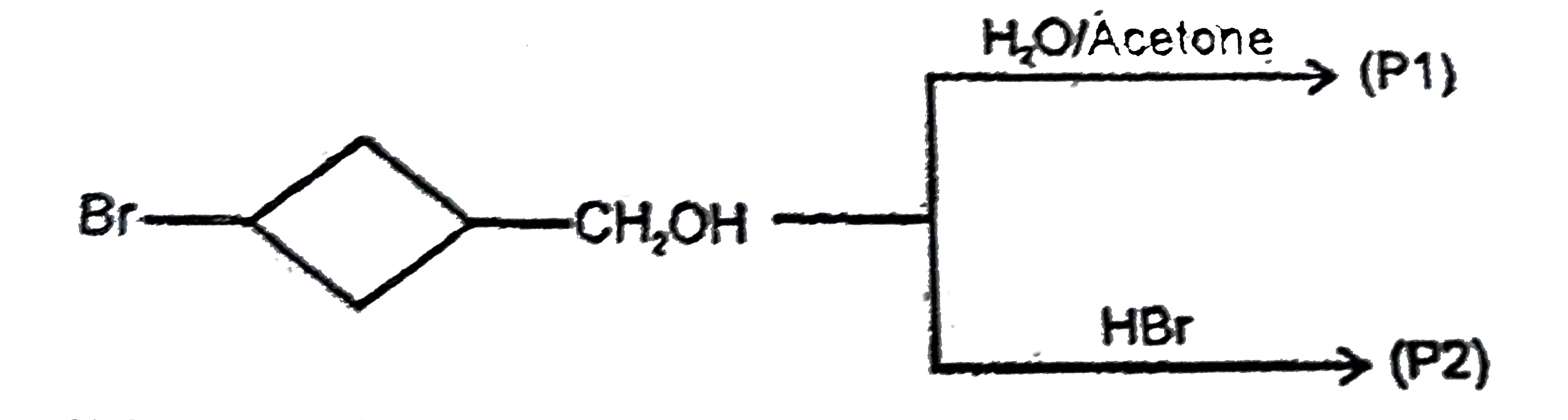
P1 and P2 are respectively :
View SolutionTwo bodies of mass 1kgand2kg have equal momentum. The ratio of their kinetic energies is:
View SolutionTwo masses 1g and 9g are moving with equal kinetic energies. The ratio of the magnitudes of their respective linear momenta is
View SolutionTwo bodies of masses m1 and m2 have equal KE. Their momenta is in the ratio
View SolutionIf Pn=cosnθ+sinnθ, then P2−P1 is equal to :
View SolutionTwo bodies of masses m1andm2 have same kinetic energy. The ratio of their momentum is
View SolutionTwo bodies of masses 4 kg and 5 kg are moving with equal momentum. Then the ratio of their respective kinetic energies is
View Solution
