Which of the following is the altitude-time graph for a projectile thrown horizontally from the top of the tower

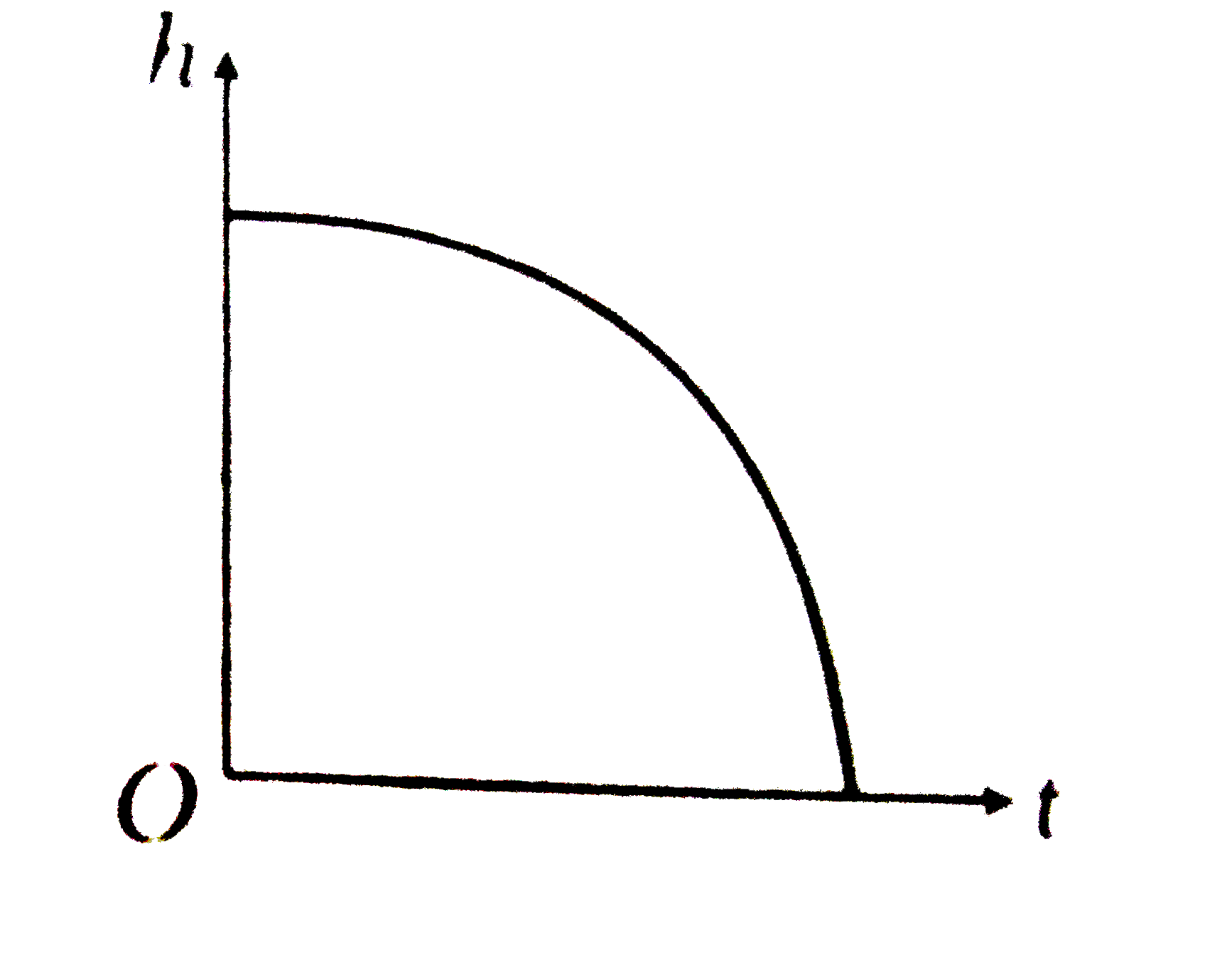
The correct Answer is:D
To determine the altitude-time graph for a projectile thrown horizontally from the top of a tower, we can follow these steps:
1. Understanding the Scenario:
- We have a tower of height H.
- A projectile is thrown horizontally from the top of the tower with an initial horizontal velocity u0.
- The initial vertical velocity of the projectile is 0 (since it is thrown horizontally).
2. Vertical Motion Analysis:
- The only force acting on the projectile in the vertical direction is gravity, which causes a downward acceleration g.
- The vertical displacement s of the projectile after time t can be described by the equation:
s=12gt2
- Since the projectile starts from height H, the height h(t) at any time t can be expressed as:
h(t)=H−12gt2
3. Graph Characteristics:
- At t=0, the height h(0)=H.
- As time increases, the height decreases due to the downward motion caused by gravity.
- The projectile will eventually reach the ground when h(t)=0. Setting the height equation to zero gives:
0=H−12gt2⟹t2=2Hg⟹t=√2Hg
- The graph of h(t) versus t will be a downward-opening parabola, starting from H and reaching 0 at t=√2Hg.
4. Identifying the Correct Graph:
- The correct altitude-time graph should start at height H and curve downwards, eventually reaching 0 at a specific time.
- Among the options provided, we need to identify the one that matches this description.
5. Conclusion:
- The correct altitude-time graph for a projectile thrown horizontally from the top of a tower is the one that starts at height H and follows a parabolic path down to 0.
Final Answer:
The correct option is the one that represents a downward-opening parabola starting from height H and reaching 0 at a certain time.
---
- We have a tower of height H.
- A projectile is thrown horizontally from the top of the tower with an initial horizontal velocity u0.
- The initial vertical velocity of the projectile is 0 (since it is thrown horizontally).
- The only force acting on the projectile in the vertical direction is gravity, which causes a downward acceleration g.
- The vertical displacement s of the projectile after time t can be described by the equation:
s=12gt2
- Since the projectile starts from height H, the height h(t) at any time t can be expressed as:
h(t)=H−12gt2
- At t=0, the height h(0)=H.
- As time increases, the height decreases due to the downward motion caused by gravity.
- The projectile will eventually reach the ground when h(t)=0. Setting the height equation to zero gives:
0=H−12gt2⟹t2=2Hg⟹t=√2Hg
- The graph of h(t) versus t will be a downward-opening parabola, starting from H and reaching 0 at t=√2Hg.
- The correct altitude-time graph should start at height H and curve downwards, eventually reaching 0 at a specific time.
- Among the options provided, we need to identify the one that matches this description.
- The correct altitude-time graph for a projectile thrown horizontally from the top of a tower is the one that starts at height H and follows a parabolic path down to 0.
The correct option is the one that represents a downward-opening parabola starting from height H and reaching 0 at a certain time.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance
12 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
Knowledge Check
A body of mass m thrown horizontally with velocity v, from the top of tower of height h touches the level ground at a distance of 250m from the foot of the tower. A body of mass 2m thrown horizontally with velocity v/2, from the top of tower of height 4h will touch the level ground at a distance x from the foot of tower. The value of x is
A250 mB500 mC125 mD250√2 m
Which of the following shows the correct expression of height d time to catch a ball dropped from the top of a tower ? (symbols have their usual meaning)
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA ball thrown horizontally with velocity v from the top of a tower of height h reaches the ground in t seconds. If another ball of double the mass is thrown horizontally with velocity 3v from the top of another tower of height 4h it reaches the ground in (seconds). In the above problem if the first ball reaches the ground at a horizontal distance d, the second ball reaches the ground at a horizontal distance
View SolutionWhich of the following x-t graphs represents the distance-time variation of a body released from the top of a buiding?
View SolutionA projectile is thrown from level ground at some angle
View SolutionA body of mass m thrown horizontally with velocity v, from the top of tower of height h touches the level ground at a distance of 250m from the foot of the tower. A body of mass 2m thrown horizontally with velocity v/2, from the top of tower of height 4h will touch the level ground at a distance x from the foot of tower. The value of x is
View Solution
