Three masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
To find the force of attraction on a unit mass placed at the fourth corner of a square formed by three masses (each of mass M) at the other three corners, we can follow these steps:
Step 1: Identify the positions of the masses
Let's denote the corners of the square as follows:
- Mass at corner A (0, 0): M
- Mass at corner B (a, 0): M
- Mass at corner C (0, a): M
- Unit mass at corner D (a, a): 1
Step 2: Calculate the gravitational force exerted by each mass on the unit mass at corner D
1. Force due to mass at corner A (F1):
- Distance from A to D = a√2 (diagonal of the square)
- Gravitational force F1=G⋅M⋅1(a√2)2=G⋅M2a2
2. Force due to mass at corner B (F2):
- Distance from B to D = a
- Gravitational force F2=G⋅M⋅1a2=G⋅Ma2
3. Force due to mass at corner C (F3):
- Distance from C to D = a
- Gravitational force F3=G⋅M⋅1a2=G⋅Ma2
Step 3: Determine the direction of the forces
- The forces F2 and F3 act horizontally and vertically, respectively, towards the unit mass at D.
- The force F1 acts diagonally towards D.
Step 4: Calculate the resultant force
1. Resultant of F2 and F3:
- Since F2 and F3 are perpendicular, we can use the Pythagorean theorem to find the resultant FR:
FR=√F22+F23=√(G⋅Ma2)2+(G⋅Ma2)2=√2(G⋅Ma2)2=G⋅M√2a2
2. Combine with F1:
- The force F1 acts at an angle of 45 degrees to the axes. The magnitude of F1 is G⋅M2a2.
- The total force FT on the unit mass at D is:
FT=FR+F1
- Since FR is diagonal and F1 is also diagonal, we can add them directly:
FT=G⋅M√2a2+G⋅M2a2
Step 5: Simplify the expression
- Combine the terms:
FT=G⋅Ma2(√2+12)
Final Answer
The total gravitational force of attraction on the unit mass at the fourth corner is:
FT=G⋅Ma2(√2+12)
Let's denote the corners of the square as follows:
- Mass at corner A (0, 0): M
- Mass at corner B (a, 0): M
- Mass at corner C (0, a): M
- Unit mass at corner D (a, a): 1
1. Force due to mass at corner A (F1):
- Distance from A to D = a√2 (diagonal of the square)
- Gravitational force F1=G⋅M⋅1(a√2)2=G⋅M2a2
- Distance from B to D = a
- Gravitational force F2=G⋅M⋅1a2=G⋅Ma2
- Distance from C to D = a
- Gravitational force F3=G⋅M⋅1a2=G⋅Ma2
- The forces F2 and F3 act horizontally and vertically, respectively, towards the unit mass at D.
- The force F1 acts diagonally towards D.
1. Resultant of F2 and F3:
- Since F2 and F3 are perpendicular, we can use the Pythagorean theorem to find the resultant FR:
FR=√F22+F23=√(G⋅Ma2)2+(G⋅Ma2)2=√2(G⋅Ma2)2=G⋅M√2a2
- The force F1 acts at an angle of 45 degrees to the axes. The magnitude of F1 is G⋅M2a2.
- The total force FT on the unit mass at D is:
FT=FR+F1
- Since FR is diagonal and F1 is also diagonal, we can add them directly:
FT=G⋅M√2a2+G⋅M2a2
- Combine the terms:
FT=G⋅Ma2(√2+12)
The total gravitational force of attraction on the unit mass at the fourth corner is:
FT=G⋅Ma2(√2+12)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples
16 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
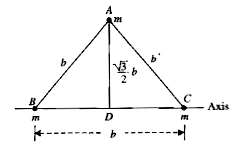 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionIf four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionThree equal masses m are placed at the three corners of an equilateral triangle of side a. find the force exerted by this system on another particle of mass m placed at (a) the mid point of a side (b) at the center of the triangle.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionThree equal masses m are placed at the three corners of an equilateral triangle of side a. The force exerted by this system on another particle of mass m placed at the mid-point of a side.
View SolutionThe moment of inertia of a system of four rods, each of length l and mass m, about the axis shown is:

View Solution
