The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

FP=0
FQ=GM1mb2
FR=G(M1+M2)c2
All are correct
The correct Answer is:D
At P, F = 0
At Q, F=GM1mb2
At R, F=G(M1+M2)mc2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises31videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.620videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
 View Solution
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
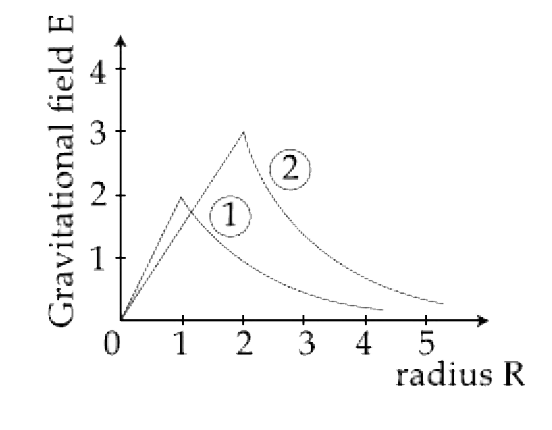 View Solution
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View SolutionFigure shows two concentric conducting shells of radii r1 and r2 carrying uniformly distributed charges q1 and q2, respectively. Find an expression for the potential of each shell.
 .View Solution
.View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.
 View Solution
View SolutionTwo concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field at a distance r ?
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionThe figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
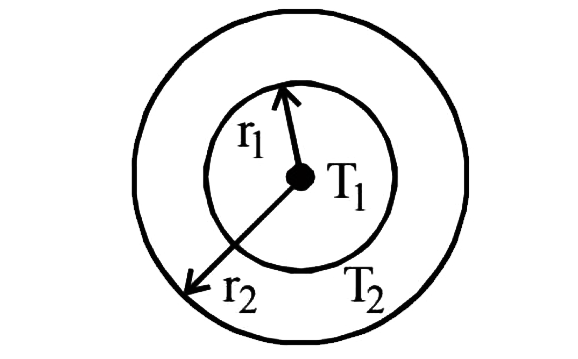 View Solution
View Solution


