Energy of a satellite in circular orbit is $E_{0}$ . The energy required to move the satellite to a circular orbit of 3 times the radius of the initial orbit is

A

$\frac{2}{3} E_{0}$

B

$2 E_{0}$

C

$\frac{E_{0}}{3}$

D

$\frac{3}{2} E_{0}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to determine the energy required to move a satellite from its initial circular orbit to a new circular orbit that is three times the radius of the initial orbit.
1. Understanding the Energy of a Satellite in Orbit:
The total mechanical energy $E$ of a satellite in a circular orbit is given by the formula:
$E = - \frac{G M m}{2 r}$
where $G$ is the gravitational constant, $M$ is the mass of the planet, $m$ is the mass of the satellite, and $r$ is the radius of the orbit.
2. Initial Energy $E_{0}$ :
Let the initial radius of the orbit be $r$ . Therefore, the energy of the satellite in the initial orbit is:
$E_{0} = - \frac{G M m}{2 r}$
3. Final Energy in the New Orbit:
The new orbit has a radius of $3 r$ . The energy of the satellite in this new orbit is:
$E_{final} = - \frac{G M m}{2 (3 r)} = - \frac{G M m}{6 r}$
4. Calculating the Change in Energy:
The work done (or energy required) to move the satellite to the new orbit is the change in energy, which can be calculated as:
$Δ E = E_{final} - E_{0}$
Substituting the values we calculated:
$Δ E = (- \frac{G M m}{6 r}) - (- \frac{G M m}{2 r})$
$Δ E = - \frac{G M m}{6 r} + \frac{G M m}{2 r}$
5. Finding a Common Denominator:
To combine these fractions, we need a common denominator. The common denominator between 6 and 2 is 6:
$Δ E = - \frac{G M m}{6 r} + \frac{3 G M m}{6 r}$
$Δ E = \frac{2 G M m}{6 r} = \frac{G M m}{3 r}$
6. Expressing in Terms of $E_{0}$ :
We know that $E_{0} = - \frac{G M m}{2 r}$ . To express $Δ E$ in terms of $E_{0}$ :
$Δ E = \frac{G M m}{3 r} = \frac{2}{3} (- \frac{G M m}{2 r}) = \frac{2}{3} E_{0}$
Final Answer:
The energy required to move the satellite to a circular orbit of three times the radius of the initial orbit is:
$Δ E = \frac{2}{3} E_{0}$

Updated on:18/9/2024

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

The period of a satellite in a circular orbit of radius R is T. What is the period of another satellite in a circular orbit of radius 4 R ?
A4 T
BT/8
CT/4
D8 T
Match the Column I with Column II
For a satellite in circular orbit

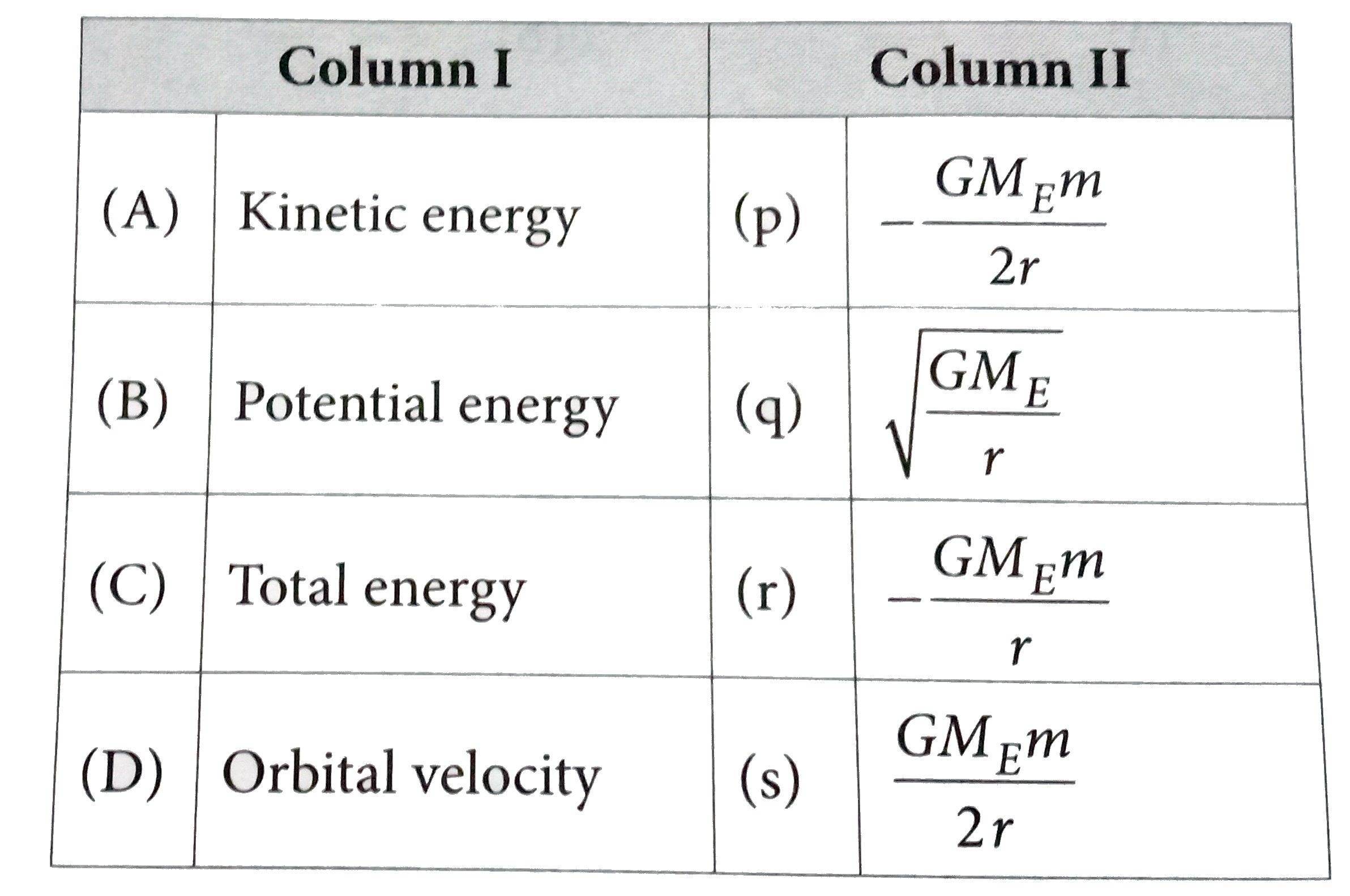
(where $M_{E}$ is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )
AA-r, B-s,C-q,D-p
BA-q,B-p,C-r,D-s
CA-p,B-q,C-s,D-r
DA-s,B-r,C-p,D-q
A satellite of mass $m$ is in a circular orbit of radius $2 R_{E}$ about the earth. The energy required to transfer it to a circular orbit of radius $4 R_{E}$ is (where $M_{E}$ and $R_{E}$ is the mass and radius of the earth respectively)
A $\frac{G M_{E} m}{2 R_{E}}$
B $\frac{G M_{E} m}{4 R_{E}}$
C $\frac{G M_{E} m}{8 R_{E}}$
D $\frac{G M_{E} m}{16 R_{E}}$

DC PANDEY ENGLISH-GRAVITATION-(A) Chapter Exercises

Home
Ask Doubt
Profile