In elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
Column-IColumn-II(A)Speed of planet(p)Remains same(B)Distance of planet from centre of sun(q)Decreases(C)Potential energy(r)Increase(D)Angular momentum about centre of sun(s)Cannot say
The correct Answer is:(A→r,B→q,C→q,D→p)
To solve the question regarding the behavior of a planet in an elliptical orbit as it moves from apogee to perigee, we will analyze each aspect mentioned in the columns.
1. Speed of the Planet (A):
- As the planet moves from apogee (farthest point from the Sun) to perigee (closest point to the Sun), its speed increases due to the conservation of angular momentum. The gravitational force acting on the planet increases as it gets closer to the Sun, causing it to accelerate.
- Conclusion: The speed of the planet increases.
- Match: (A) Speed of planet → (r) Increases.
2. Distance of the Planet from the Centre of the Sun (B):
- The distance from the Sun decreases as the planet moves from apogee to perigee. At apogee, the distance is at its maximum, and at perigee, it is at its minimum.
- Conclusion: The distance of the planet from the centre of the Sun decreases.
- Match: (B) Distance of planet from centre of Sun → (q) Decreases.
3. Potential Energy (C):
- The gravitational potential energy (U) of the planet is given by the formula U=−GMmr, where r is the distance from the Sun. As the planet gets closer to the Sun (decreasing r), the potential energy becomes more negative, indicating an increase in potential energy in terms of absolute value.
- Conclusion: The potential energy decreases (becomes more negative).
- Match: (C) Potential energy → (r) Decreases.
4. Angular Momentum about the Centre of the Sun (D):
- Angular momentum (L) is conserved in an orbiting system, meaning it remains constant as the planet moves along its elliptical path. The angular momentum can be expressed as L=mvr, and since the product of speed and radius remains constant, L does not change.
- Conclusion: The angular momentum remains the same.
- Match: (D) Angular momentum about centre of Sun → (p) Remains same.
Final Matches:
- (A) Speed of planet → (r) Increases
- (B) Distance of planet from centre of Sun → (q) Decreases
- (C) Potential energy → (s) Cannot say (it decreases)
- (D) Angular momentum about centre of Sun → (p) Remains same
- As the planet moves from apogee (farthest point from the Sun) to perigee (closest point to the Sun), its speed increases due to the conservation of angular momentum. The gravitational force acting on the planet increases as it gets closer to the Sun, causing it to accelerate.
- Conclusion: The speed of the planet increases.
- Match: (A) Speed of planet → (r) Increases.
- The distance from the Sun decreases as the planet moves from apogee to perigee. At apogee, the distance is at its maximum, and at perigee, it is at its minimum.
- Conclusion: The distance of the planet from the centre of the Sun decreases.
- Match: (B) Distance of planet from centre of Sun → (q) Decreases.
- The gravitational potential energy (U) of the planet is given by the formula U=−GMmr, where r is the distance from the Sun. As the planet gets closer to the Sun (decreasing r), the potential energy becomes more negative, indicating an increase in potential energy in terms of absolute value.
- Conclusion: The potential energy decreases (becomes more negative).
- Match: (C) Potential energy → (r) Decreases.
- Angular momentum (L) is conserved in an orbiting system, meaning it remains constant as the planet moves along its elliptical path. The angular momentum can be expressed as L=mvr, and since the product of speed and radius remains constant, L does not change.
- Conclusion: The angular momentum remains the same.
- Match: (D) Angular momentum about centre of Sun → (p) Remains same.
- (A) Speed of planet → (r) Increases
- (B) Distance of planet from centre of Sun → (q) Decreases
- (C) Potential energy → (s) Cannot say (it decreases)
- (D) Angular momentum about centre of Sun → (p) Remains same
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises68videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot sayView SolutionMatch the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2rView SolutionMatch the following
Column-IColumn-II(A)Kepler's first law(p)T2∝r3(B)Kepler's second law(q)Areal velocity is constant(C)Kepler's third law(r)Orbit of planet is ellipticalView SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
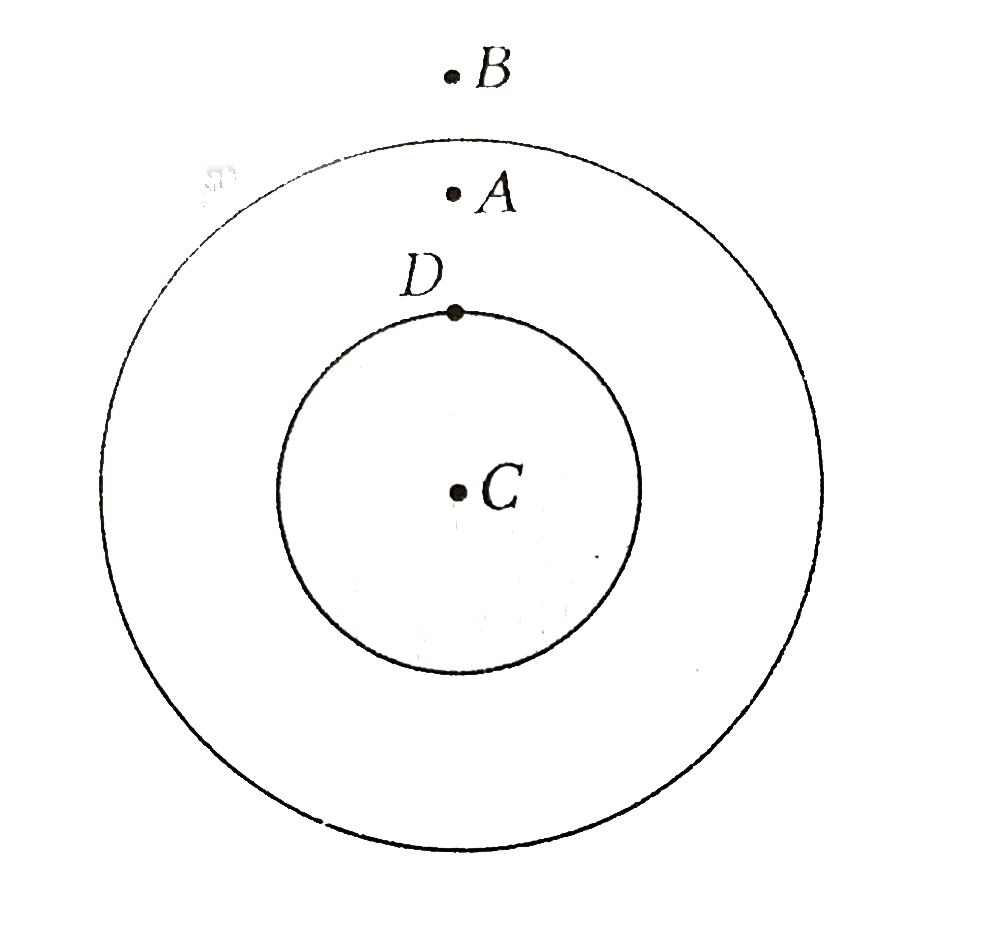
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)NoneView SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinityView SolutionMatch the Column-I with Column-II :
Column-IColumn-II(a)Mole fraction(p)mol kg−1(b)Molality(q)Depends on temperature(c)Molarity(r)Unitless(d)Normality(s)Independent of temperatureView SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four timesView SolutionMatch the following
Column-IColumn-II(A)Enthalpy(p)Extensive property(B)Entropy(q)H - TS(C)Free energy(r)E + PV(D)Pressure(s)Intensive propertyView SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)Constant positive acceleration(p)Speed may increase(B)Constant negative acceleration(q)Speed may decrease(C)Constant displacement(r)Speed is zero(D)Constant slope of a-t graph(s)Speed must increase(t)Speed must decrease∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA solid sphere is rotating about an axis shown in figure. An insect follows the dotted path on the circumference of sphere as shown in the figure.
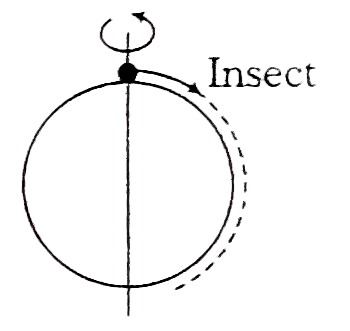
Column-IColumn-II(A)Moment of inertia(p)Will remain constant(B)Angular velocity(q)Will first increase, then decrease(C)Angular momentum(r)Will first decrease then increase(D)Rotational kinetic energy(s)Will continuously decrease(t)Will continuously increaseView Solution

