Assertion : The centre of semicircular ring of mass m and radius R is the origin O. The potential at origin is −GmR

Reason : The gravitational field strength is towards Y-axis.
If both Assertin and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:B
Step by step video & image solution for Assertion : The centre of semicircular ring of mass m and radius R is the origin O. The potential at origin is -(Gm)/(R) Reason : The gravitational field strength is towards Y-axis. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
For a uniform ring of mass M and radius R at its centre
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionThe M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View SolutionGravitational potential at a distance 'r' from a point mass 'm' is
V=−GMr
Find gravitational field strength at that point.
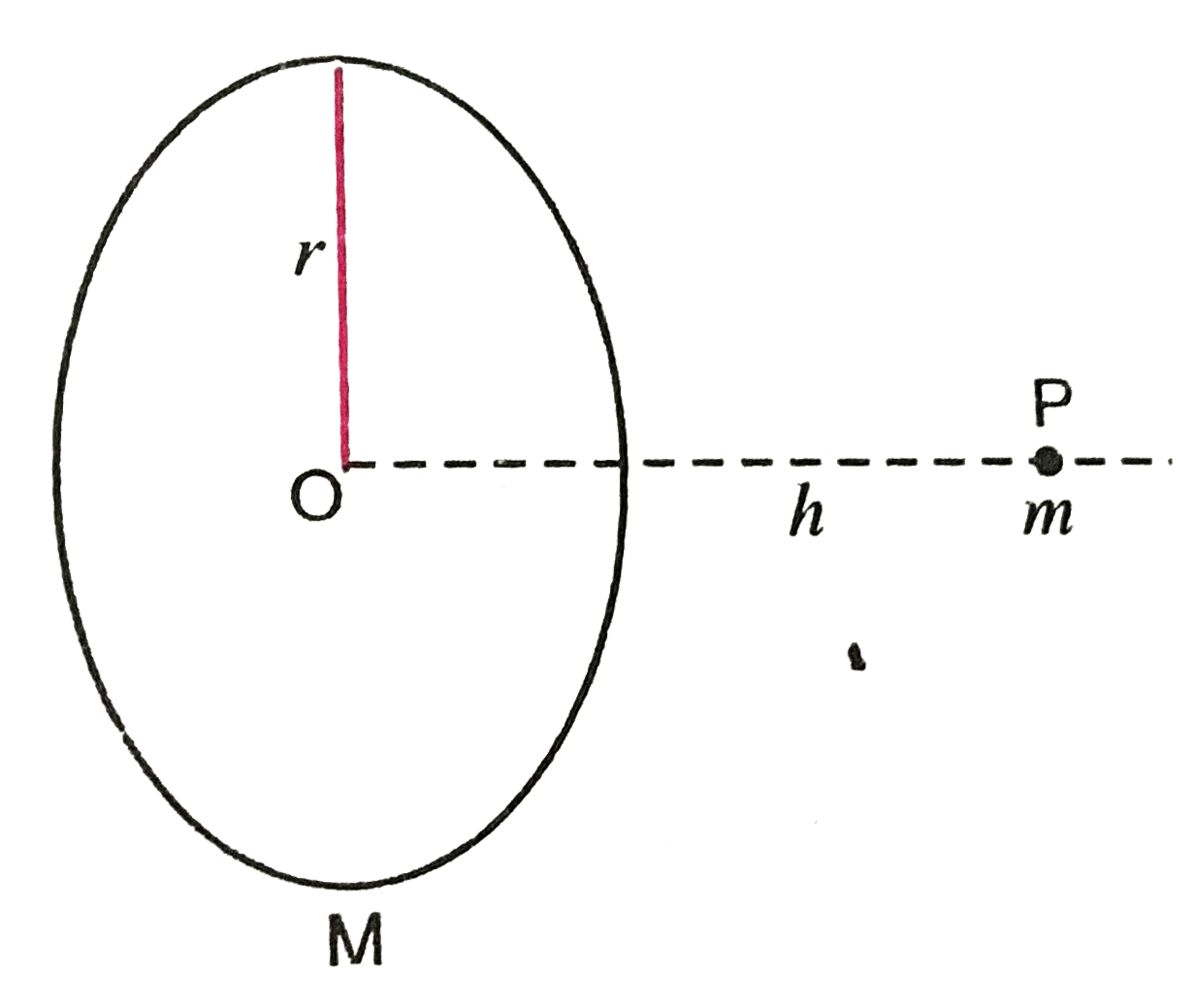
View SolutionA mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig.
If the mass is removed futher away such that OP becomes 2h, by what factor the force of gravitational will decrease, if h=r ?
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
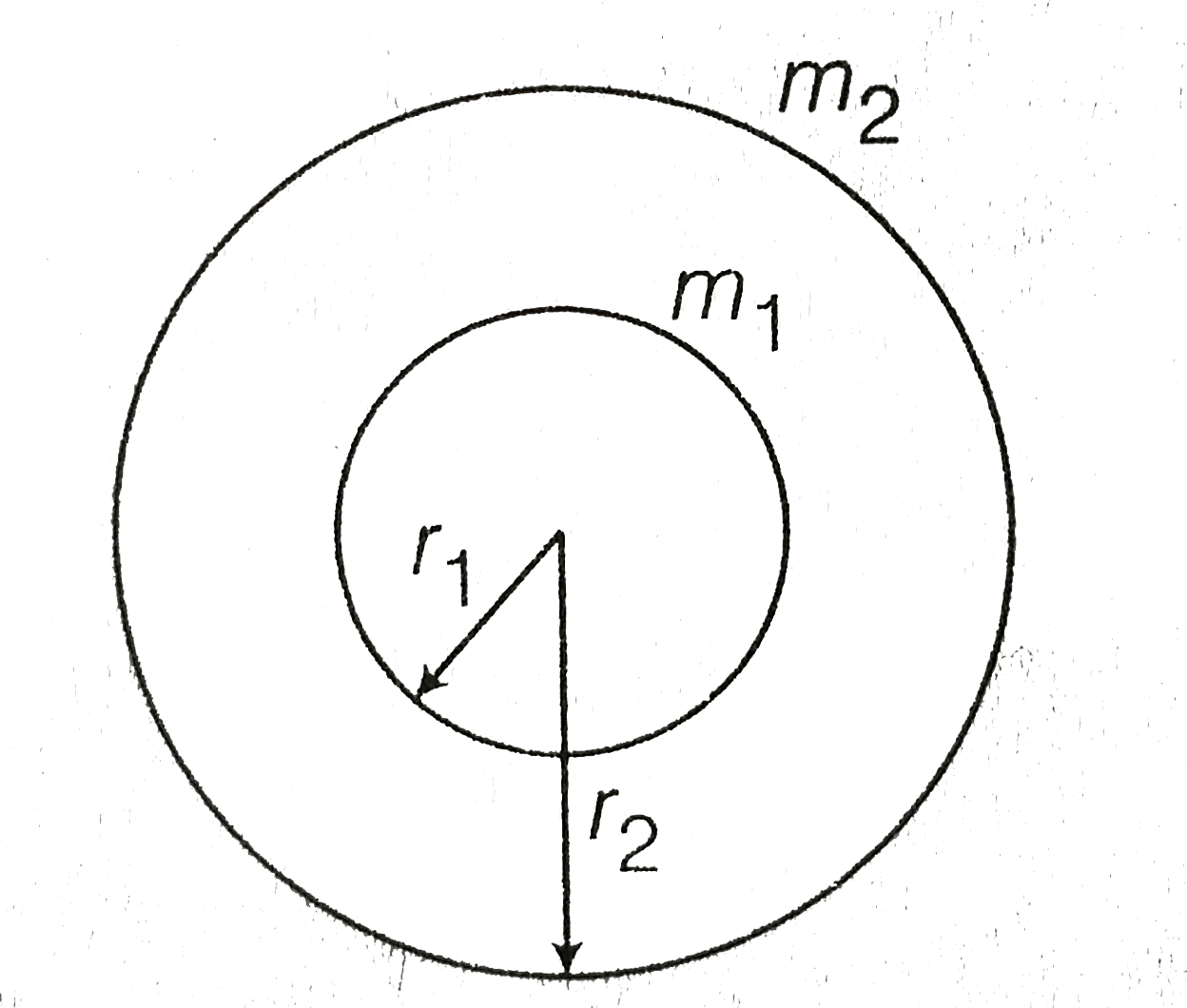
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionAssertion : In moving from centre of a solid sphere to its surface, gravitational potential increases.
Reason : Gravitational field strength increase.
View Solution