A and B are two points separately by a distance 5cm. Two charges 10μCand20μC are placed at A and B. The resultant electric intensity at a point P outside the charges at a distance 5cm from 10μC is
54×106N/C away from 10μC
56×106N/C towards 10μC
9×106N/C away from 10μC
zero
The correct Answer is:A
To solve the problem, we need to find the resultant electric field intensity at point P, which is located 5 cm from the charge of 10 µC (microcoulombs) at point A. The charge at point B is 20 µC and is located 5 cm away from point A.
1. Identify the Charges and Their Positions:
- Charge at point A (Q1) = 10 µC = 10×10−6 C
- Charge at point B (Q2) = 20 µC = 20×10−6 C
- Distance between A and B = 5 cm = 0.05 m
- Distance from point P to charge A = 5 cm = 0.05 m
- Distance from point P to charge B = Distance from A to B + Distance from A to P = 0.05+0.05=0.10 m
2. Calculate the Electric Field due to Charge A (E1):
The electric field (E) due to a point charge is given by the formula:
E=14πϵ0⋅Qr2
Where:
- ϵ0 (permittivity of free space) = 8.85×10−12C2/N m2
- Q = charge
- r = distance from the charge
For charge A:
E1=14πϵ0⋅10×10−6(0.05)2
E1=9×109(0.0025)⋅10×10−6
E1=9×109⋅4×103=36×106N/C
3. Calculate the Electric Field due to Charge B (E2):
For charge B:
E2=14πϵ0⋅20×10−6(0.10)2
E2=9×109(0.01)⋅20×10−6
E2=9×109⋅2×106=18×106N/C
4. Determine the Direction of the Electric Fields:
- Both electric fields E1 and E2 are directed towards the positive charges (since they are positive), which means they are directed towards point B.
5. Calculate the Resultant Electric Field (E):
Since both fields are in the same direction, we can add them:
E=E1+E2=36×106+18×106=54×106N/C
6. Final Result:
The resultant electric intensity at point P is 54×106N/C directed away from the charge at A.
- Charge at point A (Q1) = 10 µC = 10×10−6 C
- Charge at point B (Q2) = 20 µC = 20×10−6 C
- Distance between A and B = 5 cm = 0.05 m
- Distance from point P to charge A = 5 cm = 0.05 m
- Distance from point P to charge B = Distance from A to B + Distance from A to P = 0.05+0.05=0.10 m
The electric field (E) due to a point charge is given by the formula:
E=14πϵ0⋅Qr2
Where:
- ϵ0 (permittivity of free space) = 8.85×10−12C2/N m2
- Q = charge
- r = distance from the charge
E1=14πϵ0⋅10×10−6(0.05)2
E1=9×109(0.0025)⋅10×10−6
E1=9×109⋅4×103=36×106N/C
For charge B:
E2=14πϵ0⋅20×10−6(0.10)2
E2=9×109(0.01)⋅20×10−6
E2=9×109⋅2×106=18×106N/C
- Both electric fields E1 and E2 are directed towards the positive charges (since they are positive), which means they are directed towards point B.
Since both fields are in the same direction, we can add them:
E=E1+E2=36×106+18×106=54×106N/C
The resultant electric intensity at point P is 54×106N/C directed away from the charge at A.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I80videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
Similar Questions
Two charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
View SolutionTwo equal and opposite charges of magnitude 0.2μC are 15 cm apart, the magnitude and direction of the resultant electric intensity at a point midway between the charges is
View SolutionTwo point charges 2μC and −2μC are placed at point A and B as shown in figure. Find out electric field intensity at points C and D. [All the distances are measured in meter].
 View Solution
View SolutionTwo point charges of 20μC and 80μC are 10 cm apart where will the electric field strength be zero on the line joining the charges from 20μC charge
View SolutionTwo charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View Solutionfind the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
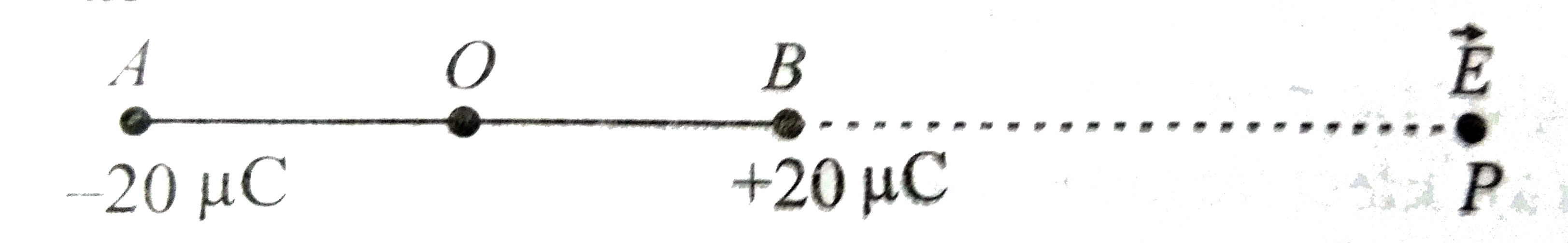 View Solution
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric. field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View Solution

