There is an air filled 1pF parallel plate capacitor. When the plate separation is doubled and the space is filled with wax, the capacitance increases to 2pF. The dielectric constant of wax is
2
4
6
8
The correct Answer is:B
To solve the problem, we need to understand the relationship between capacitance, plate separation, and the dielectric constant. Let's break it down step by step.
Step 1: Understand the formula for capacitance
The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵ0d
where:
- C is the capacitance,
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
Step 2: Initial conditions
Initially, we have an air-filled capacitor with a capacitance of 1 pF (picoFarad). Therefore, we can write:
C1=Aϵ0d=1 pF
Step 3: Change in conditions
When the plate separation is doubled, the new separation d′ becomes 2d. The space between the plates is then filled with wax, which has a dielectric constant k. The new capacitance C2 can be expressed as:
C2=Akϵ0d′
Substituting d′=2d:
C2=Akϵ02d
Step 4: Relate the new capacitance to the old capacitance
Since we know that the new capacitance C2 is 2 pF, we can set up the equation:
Akϵ02d=2 pF
Step 5: Substitute the initial capacitance
From the initial condition, we have:
Aϵ0d=1 pF
Now, we can express Aϵ0 in terms of d:
Aϵ0=1 pF⋅d
Step 6: Substitute into the new capacitance equation
Substituting Aϵ0 into the equation for C2:
C2=1 pF⋅d⋅k2d=k2 pF
Setting this equal to the new capacitance:
k2=2 pF
Step 7: Solve for the dielectric constant k
Multiplying both sides by 2 gives:
k=4
Conclusion
The dielectric constant of the wax is k=4.
---
The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵ0d
where:
- C is the capacitance,
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
Initially, we have an air-filled capacitor with a capacitance of 1 pF (picoFarad). Therefore, we can write:
C1=Aϵ0d=1 pF
When the plate separation is doubled, the new separation d′ becomes 2d. The space between the plates is then filled with wax, which has a dielectric constant k. The new capacitance C2 can be expressed as:
C2=Akϵ0d′
Substituting d′=2d:
C2=Akϵ02d
Since we know that the new capacitance C2 is 2 pF, we can set up the equation:
Akϵ02d=2 pF
From the initial condition, we have:
Aϵ0d=1 pF
Now, we can express Aϵ0 in terms of d:
Aϵ0=1 pF⋅d
Substituting Aϵ0 into the equation for C2:
C2=1 pF⋅d⋅k2d=k2 pF
Setting this equal to the new capacitance:
k2=2 pF
Multiplying both sides by 2 gives:
k=4
The dielectric constant of the wax is k=4.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An air filled parallel capacitor has capacity of 2pF. The separation of the plates is doubled and the interspaces between the plates is filled with wax. If the capacity is increased to 6pF, the dielectric constant of was is
View SolutionWhen a parallel plate capacitor is filled with wax after separation between plates is doubled, its capacitance becomes twice. What is the dielectric constant of wax?
View Solution
Knowledge Check
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
The figure shows a parallel-plate capacitor having square plates of edge a and plate-separation di The gap between the plates is filled with a directric of dielectric constant k which varies as K=K0+αx parallel to an edge as where K and α are constants and x is the distance from the left end. Calaculate the capacitance.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as where K and a are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a isngle dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
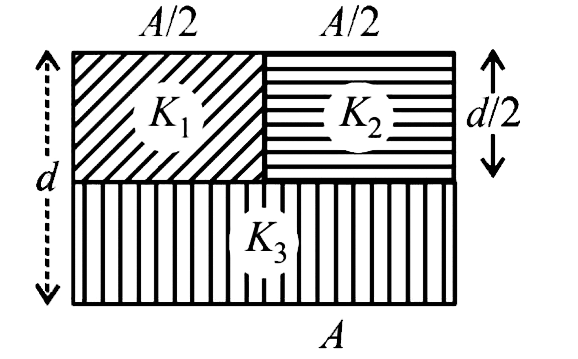
View Solution
