Two concentric spherical conducting shells of radii r and R carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
zero
To solve the problem of finding the final charge on the inner shell after connecting two concentric spherical conducting shells with charges q and Q, we can follow these steps:
1. Understanding the System: We have two concentric spherical conducting shells. The inner shell has a radius r and carries a charge q. The outer shell has a radius R and carries a charge Q. When connected by a conducting wire, charges can redistribute between the two shells.
Hint: Visualize the arrangement of the shells and their charges.
2. Connecting the Shells: When the two shells are connected by a conducting wire, they will reach the same electric potential. This is because conductors in electrostatic equilibrium must be at the same potential.
Hint: Remember that charges will redistribute until the potential is equal.
3. Electric Field Inside the Conductors: Inside a conductor, the electric field is zero. This means that any excess charge will reside on the outer surface of the conductors. Therefore, the charge on the inner shell will not affect the charge distribution on the outer shell.
Hint: Recall that the electric field inside a conductor in electrostatic equilibrium is zero.
4. Charge Redistribution: The total charge in the system before connecting the shells is q+Q. After connecting, the total charge will redistribute between the inner and outer shells. However, the inner shell must have zero net charge because any charge on it would create an electric field inside the conductor, which contradicts the condition of electrostatic equilibrium.
Hint: Consider the implications of having a net charge on the inner shell.
5. Final Charge on the Inner Shell: Since the inner shell must have zero net charge after the connection, we conclude that the final charge on the inner shell is 0.
Hint: Think about how charges behave in conductors and the requirement for electrostatic equilibrium.
Final Answer:
The final charge on the inner shell is 0.
The final charge on the inner shell is 0.
Similar Questions
Two concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
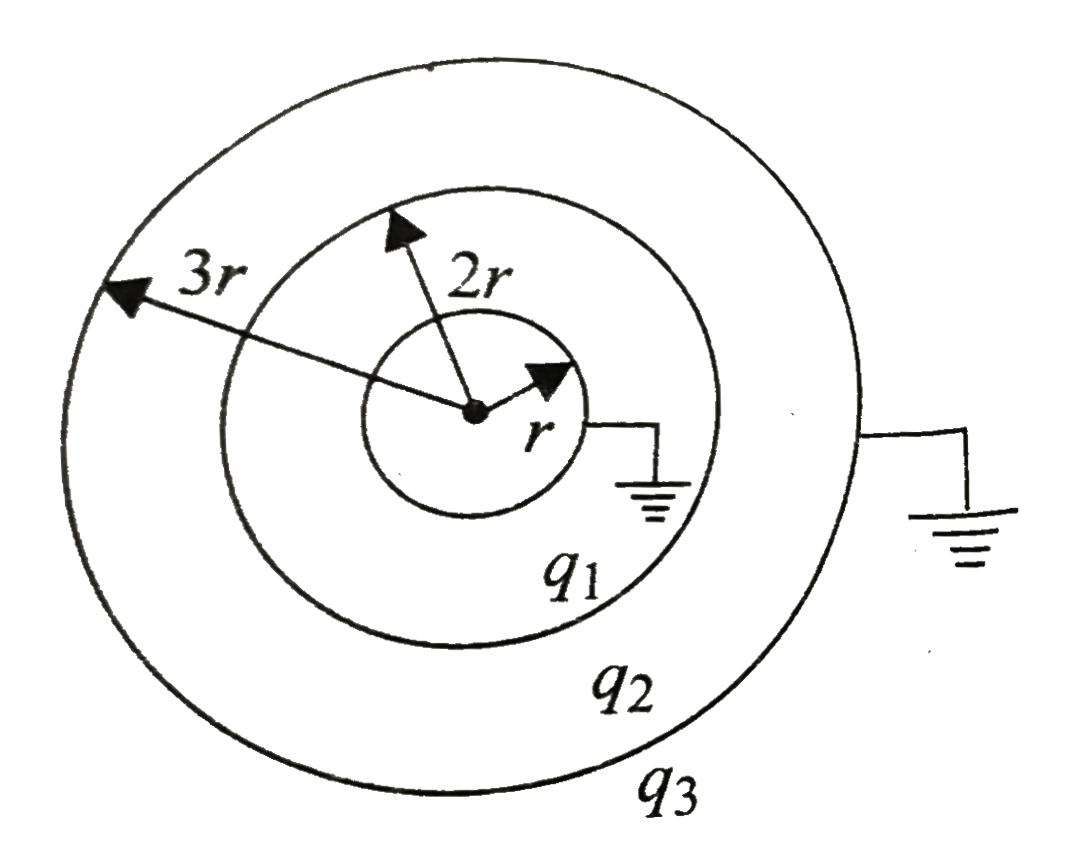
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
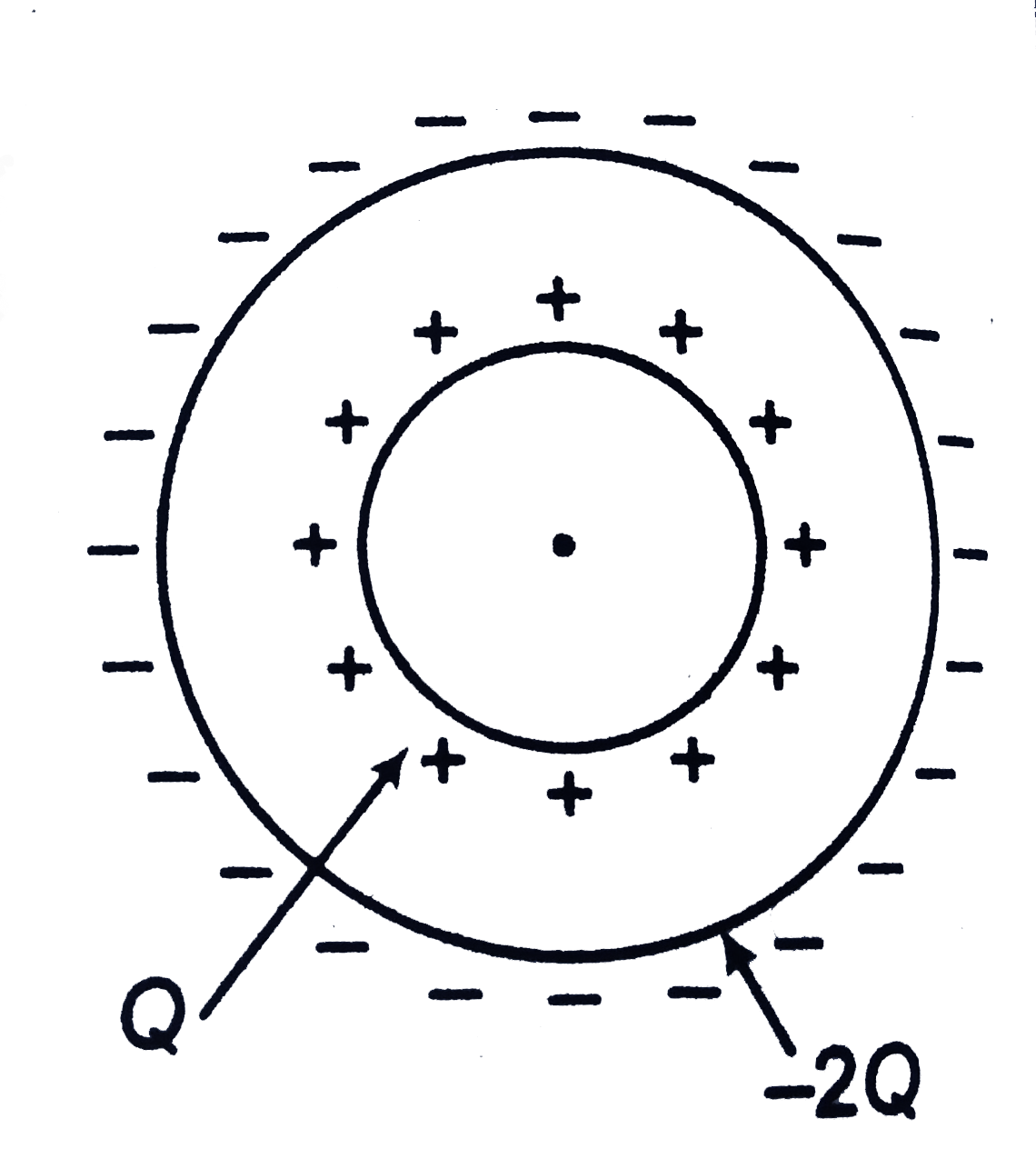
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
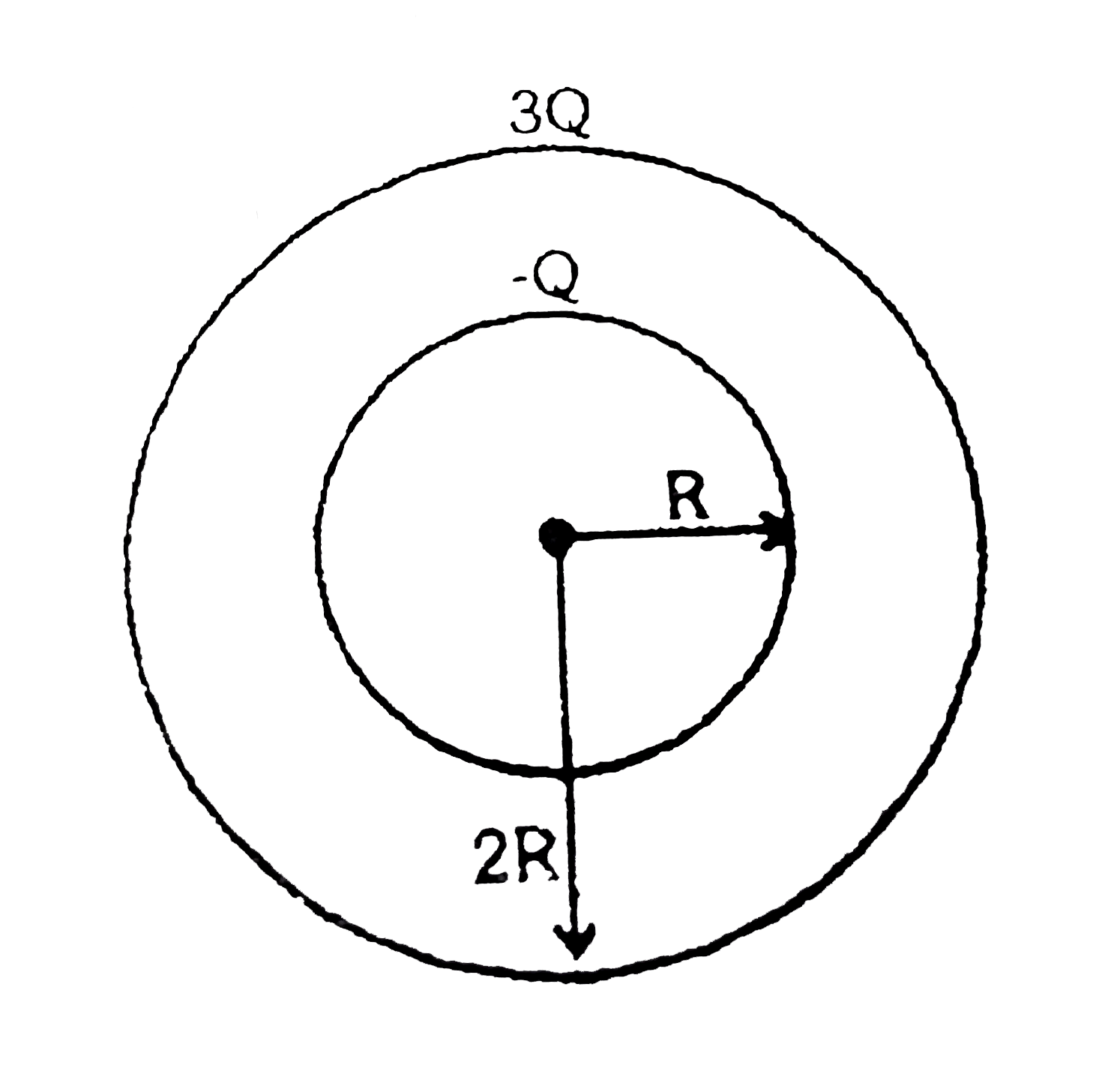
View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View Solution
