Drift velocity vd varies with the intensity of electric field as per their relation
vd∝E
vd∝1E
vd=constant
vd∝E2
The correct Answer is:A
To solve the question regarding the relationship between drift velocity vd and the intensity of the electric field E, we can follow these steps:
1. Understanding Drift Velocity:
Drift velocity vd is the average velocity that charged particles, such as electrons, attain due to an electric field.
2. Formula for Drift Velocity:
The drift velocity can be expressed using the formula:
vd=eVmLτ
where:
- e is the charge of the electron,
- V is the potential difference,
- m is the mass of the electron,
- L is the length of the conductor,
- τ is the relaxation time.
3. Relating Potential Difference to Electric Field:
The potential difference V can be expressed in terms of the electric field E and the length L of the conductor:
V=E⋅L
4. Substituting into Drift Velocity Formula:
Substituting V into the drift velocity formula gives:
vd=e(E⋅L)mLτ
5. Simplifying the Expression:
In the equation, the length L cancels out:
vd=eEmτ
6. Identifying the Relationship:
From the simplified equation, we can see that:
vd∝E
This indicates that the drift velocity vd is directly proportional to the electric field intensity E when e, m, and τ are constants.
7. Conclusion:
Therefore, the relationship between drift velocity and electric field intensity is:
vd is directly proportional to E
Final Answer:
The correct option is Option 1: vd is proportional to the electric field intensity E.
Drift velocity vd is the average velocity that charged particles, such as electrons, attain due to an electric field.
The drift velocity can be expressed using the formula:
vd=eVmLτ
where:
- e is the charge of the electron,
- V is the potential difference,
- m is the mass of the electron,
- L is the length of the conductor,
- τ is the relaxation time.
The potential difference V can be expressed in terms of the electric field E and the length L of the conductor:
V=E⋅L
Substituting V into the drift velocity formula gives:
vd=e(E⋅L)mLτ
In the equation, the length L cancels out:
vd=eEmτ
From the simplified equation, we can see that:
vd∝E
This indicates that the drift velocity vd is directly proportional to the electric field intensity E when e, m, and τ are constants.
Therefore, the relationship between drift velocity and electric field intensity is:
vd is directly proportional to E
The correct option is Option 1: vd is proportional to the electric field intensity E.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Suppose the drift velocity vd in a material varied with the applied electric field E as vd∝√E. Then V – I graph for a wire made of such a material is best given by :
View SolutionThe SI unit of electric field intensity is
View SolutionA charged oil drop falls with terminal velocity v0 in the absence of electric field. An electric field E keeps it stationary. The drop acquires charge 3q, it starts moving upwards with velocity v0. The initial charge on the drop is
View SolutionAn electron is projected with velocity v0 in a unifrom electric field E perpendicular to the field Again it is projectced with velocity v0 perpendicular to a unifrom magnetic field B. if r1 is initial radius of curvature just after entering in the electric field and r2 is initial radius of curvature just after entering in magnetic field then the ratio r1/r2 is equal to .
View SolutionDerive an expression for intensity of electric field are a point in broadside position or on an equatorial line of an electric dipole.
View SolutionIf E is the electric field intensity of an electrostatic field, then the electrostatic energy density is proportional to
View SolutionAn electron projectes with velocity →v=v0ˆi in the electric field →E=E0ˆj. There the path followed by the electron E0.
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
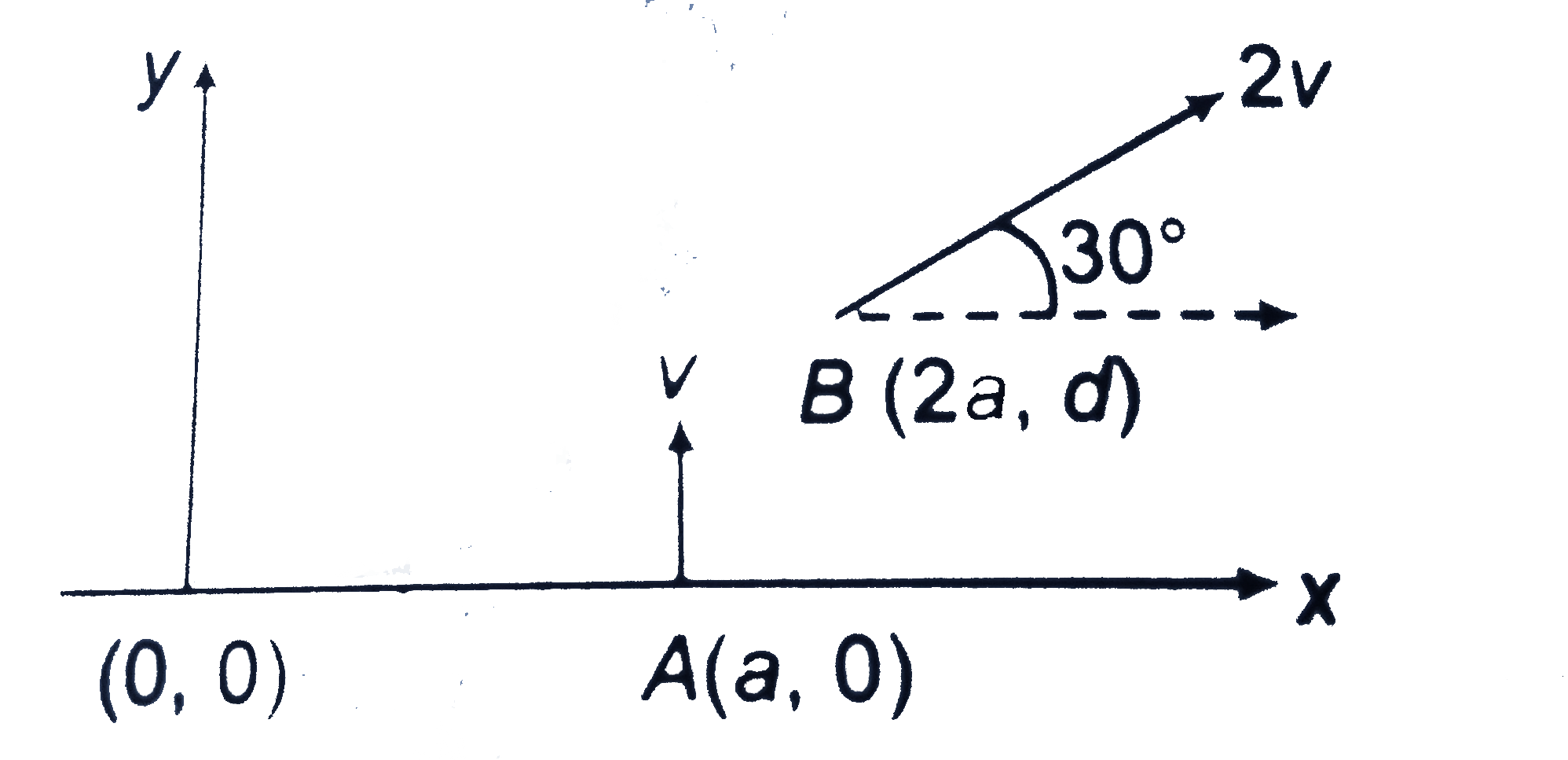
View SolutionDefine drift velocity of free electron . If relaxation time is r then write a vector relation b etween drift velocity and electric field.
View SolutionIn a region where intensity of electric field is 5NC−140 lines of electric force are crossing per square metre. The number of lines crossing per square metre where intensity of electric field is 10NC−1 will be
View Solution