Two concentric circular coils of ten turns each are situated in the same plane. Their radii are 20 and 40cm and they carry respectively 0.2 and 0.3 ampere current in opposite direction. The magnetic field in Wb/m3 at the centre is
(35/4)μ0
(μ0/80)
(7/80)μ0
(54)μ0
The correct Answer is:B
To find the magnetic field at the center of two concentric circular coils carrying currents in opposite directions, we can use the formula for the magnetic field due to a circular coil at its center:
B=μ0nI2R
where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- n is the number of turns,
- I is the current,
- R is the radius of the coil.
Step 1: Identify the parameters for both coils
- For coil 1:
- Number of turns n1=10
- Radius R1=20cm=0.2m
- Current I1=0.2A
- For coil 2:
- Number of turns n2=10
- Radius R2=40cm=0.4m
- Current I2=0.3A
Step 2: Calculate the magnetic field due to each coil
Using the formula for the magnetic field:
1. Magnetic field due to coil 1:
B1=μ0n1I12R1=4π×10−7×10×0.22×0.2
Simplifying this:
B1=4π×10−7×10×0.20.4=4π×10−7×10×0.51=2π×10−6T
2. Magnetic field due to coil 2:
B2=μ0n2I22R2=4π×10−7×10×0.32×0.4
Simplifying this:
B2=4π×10−7×10×0.30.8=4π×10−7×10×0.3751=1.5π×10−6T
Step 3: Determine the net magnetic field at the center
Since the currents are in opposite directions, the net magnetic field B at the center will be the difference between B1 and B2:
B=B1−B2=2π×10−6−1.5π×10−6=0.5π×10−6T
Step 4: Convert to Wb/m³
Since 1T=1Wb/m2, we can express the magnetic field in Wb/m³ as:
B=0.5π×10−6Wb/m2
Final Answer
B≈1.57×10−6Wb/m2
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- n is the number of turns,
- I is the current,
- R is the radius of the coil.
- For coil 1:
- Number of turns n1=10
- Radius R1=20cm=0.2m
- Current I1=0.2A
- Number of turns n2=10
- Radius R2=40cm=0.4m
- Current I2=0.3A
Using the formula for the magnetic field:
B1=μ0n1I12R1=4π×10−7×10×0.22×0.2
Simplifying this:
B1=4π×10−7×10×0.20.4=4π×10−7×10×0.51=2π×10−6T
B2=μ0n2I22R2=4π×10−7×10×0.32×0.4
Simplifying this:
B2=4π×10−7×10×0.30.8=4π×10−7×10×0.3751=1.5π×10−6T
Since the currents are in opposite directions, the net magnetic field B at the center will be the difference between B1 and B2:
B=B1−B2=2π×10−6−1.5π×10−6=0.5π×10−6T
Since 1T=1Wb/m2, we can express the magnetic field in Wb/m³ as:
B=0.5π×10−6Wb/m2
B≈1.57×10−6Wb/m2
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
Two concentric coils of 10 turns each are placed in the same plane. Their radii are 20 cm and 40 cm and carry 0.2 A and 0.3 A current respectively in opposite directions. The magnetic induction (in tesla) at the centre is
View SolutionTwo concentric coplaner circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite directions (one clockwise and the other anticlockwise .) The magnetic induction at the centre of the loops is half that due to i1 alone at the centre . If r2=2r , the value of i2/i1 is
View Solution
Knowledge Check
The electric current in a circular coil of two turns produced a magnetic induction of 0.2 T at its centre. The coil is unwound and then rewound into a circular coil of four turns. If same current flows in the coil, the magnetic induction at the centre of the coil now is
A0.2TB0.4TC0.6TD0.8TA circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
Two concentric coils each of radius equal to 2πcm are placed at right angles to each other 3ampereand4ampere are the currents flowing in each coil respectively. The magnetic induction in weber/m2 at the centre of the coils will be
(μ0=4π×10−7Wb/A.m)
View SolutionTwo concentric coils each of radius equal to 2πcm are placed at right angles to each other 3ampereand4ampere are the currents flowing in each coil respectively. The magnetic induction in weber/m2 at the centre of the coils will be
(μ0=4π×10−7Wb/A.m)
View SolutionTwo coplanar concentric circular coils of radii r and 2r, have the same number of turns n. The smaller coil carries a clockwise current i, while the larger coil carries an anticlockwise current 2i. The magnetic field induction at the centre is
View SolutionAn otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
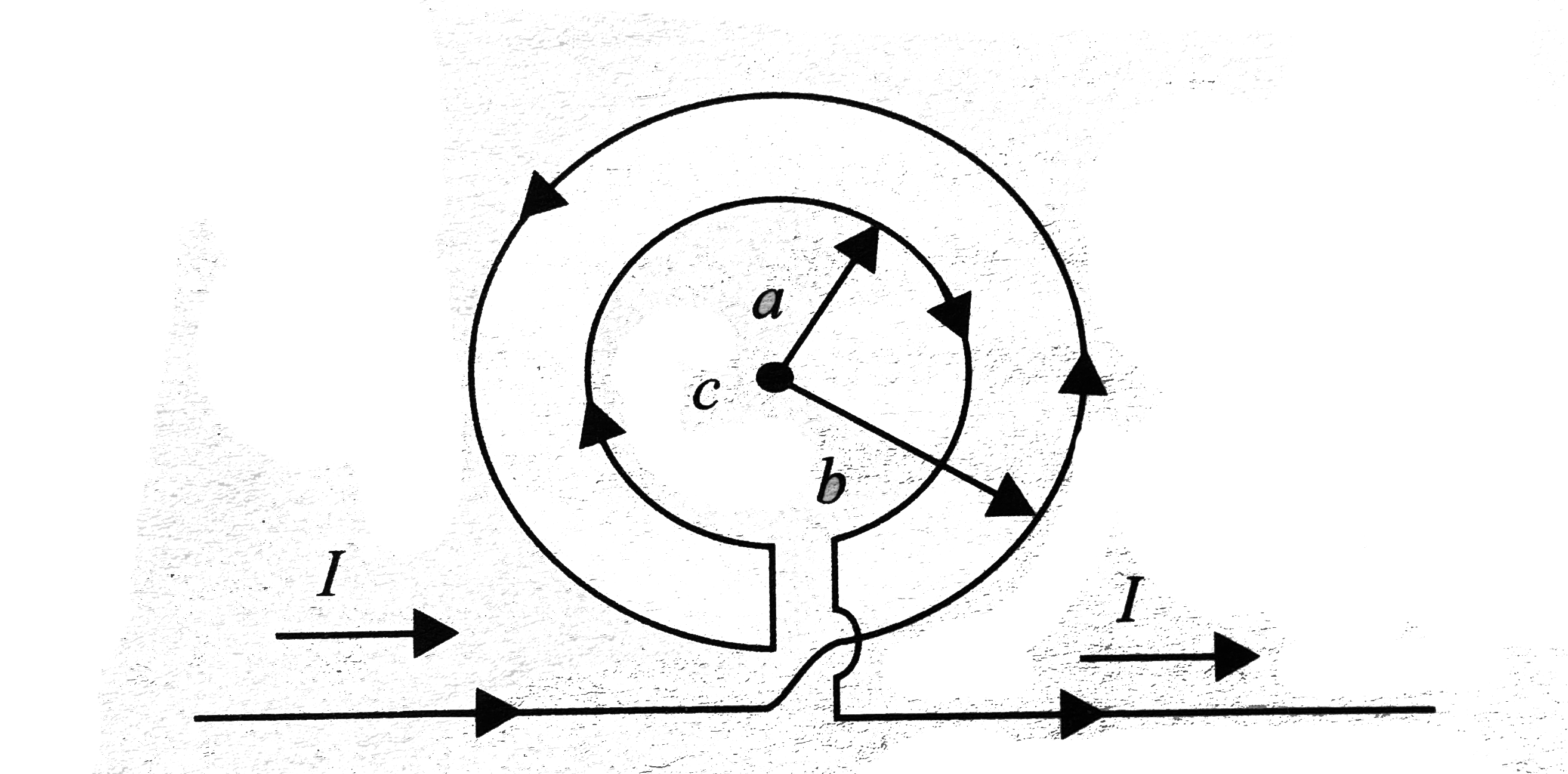
View SolutionTwo Concentric circular coils X and Y of radii 16cm and 10cm lie in the same vertical plane containing N−S direction X has 20 turns and carries 16A.Y has 25 turns & carries 18A.X has current in anticlockwise direction and Y has current in clockwise direction for the observer, looking at the coils facing the west. The magnitude of net magnetic field at their common center is?
View SolutionTwo circular coils of wire each having a radius of 4cm and 10turns have a common axis and are 3cm apart If a current of 1A passes through each coil in the opposite direction find the magnetic induction
(i) At the center of either coil
(ii) At a point on the axis, midway between them .
View Solution
