A current of ampere is flowing in a wire of length . A force of acts on it when it is placed in a uniform magnetic field of tesla. The angle between the magnetic field and the direction of the current is
The correct Answer is:A
To find the angle between the magnetic field and the direction of the current in a wire, we can use the formula for the force acting on a current-carrying wire in a magnetic field:
F=I⋅L⋅B⋅sin(θ)
Where:
- F is the force acting on the wire (in Newtons),
- I is the current flowing through the wire (in Amperes),
- L is the length of the wire (in meters),
- B is the magnetic field strength (in Teslas),
- θ is the angle between the magnetic field and the direction of the current.
Step 1: Identify the given values
From the problem, we have:
- F=15N
- I=10A
- L=1.5m
- B=2T
Step 2: Rearrange the formula to solve for sin(θ)
We can rearrange the formula to isolate sin(θ):
sin(θ)=FI⋅L⋅B
Step 3: Substitute the known values into the equation
Now, substitute the known values into the equation:
sin(θ)=1510⋅1.5⋅2
Step 4: Calculate the denominator
Calculate I⋅L⋅B:
I⋅L⋅B=10⋅1.5⋅2=30
Step 5: Calculate sin(θ)
Now substitute this back into the equation for sin(θ):
sin(θ)=1530=12
Step 6: Find θ
To find θ, we take the inverse sine:
θ=sin−1(12)
From trigonometric values, we know:
θ=30∘
Conclusion
Thus, the angle between the magnetic field and the direction of the current is 30∘.
- F is the force acting on the wire (in Newtons),
- I is the current flowing through the wire (in Amperes),
- L is the length of the wire (in meters),
- B is the magnetic field strength (in Teslas),
- θ is the angle between the magnetic field and the direction of the current.
From the problem, we have:
- F=15N
- I=10A
- L=1.5m
- B=2T
We can rearrange the formula to isolate sin(θ):
Now, substitute the known values into the equation:
Calculate I⋅L⋅B:
Now substitute this back into the equation for sin(θ):
To find θ, we take the inverse sine:
Thus, the angle between the magnetic field and the direction of the current is 30∘.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
Knowledge Check
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
The force exerted on a current-carrying wire placed in magnetic field is zero when the angle between the wire and the direction of magnetic field is :
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
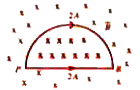
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionIf a wire of length l meter placed in uniform magnetic field 1.5 Tesla at angle 30∘ with magnetic field. The current in a wire 10 amp. Then force on a wire will be
View Solution
