A charged particle P leaves the origin with speed v=v0 at some inclination with the x-axis. There is a uniform magnetic field B along the x-axis. P strikes a fixed target T on the x-axis for a minimum value of B=B0. P will also strike T if
B=2B0,v=2v0
B=2B0,v=v0
Both are correct
Both are wrong
The correct Answer is:A
To solve the problem, we need to analyze the motion of the charged particle P in a magnetic field. The particle leaves the origin with a speed v=v0 at an angle θ with the x-axis, and it is subjected to a uniform magnetic field B along the x-axis. We want to determine the conditions under which the particle strikes a fixed target T on the x-axis.
1. Understanding the Motion of the Charged Particle:
The charged particle P experiences a magnetic force due to the magnetic field B. The magnetic force F on a charged particle is given by:
F=q(v×B)
where q is the charge of the particle, v is its velocity, and B is the magnetic field.
2. Determining the Components of Velocity:
The velocity v can be resolved into two components:
- vx=v0cosθ (along the x-axis)
- vy=v0sinθ (along the y-axis)
3. Calculating the Magnetic Force:
Since the magnetic field B is along the x-axis, the magnetic force will act in the y-direction:
Fy=q(vyB)=q(v0sinθB)
4. Finding the Radius of the Circular Motion:
The particle will undergo circular motion in the y-z plane due to the magnetic force. The radius r of the circular motion can be expressed as:
r=mvyqB=m(v0sinθ)qB
5. Determining the Pitch of the Helix:
The pitch P of the helical path is the distance traveled along the x-axis in one complete revolution. The pitch is given by:
P=2πmqBvx=2πmqB(v0cosθ)
6. Setting the Condition for Striking the Target:
For the particle P to strike the target T on the x-axis, the pitch must be such that the particle returns to the x-axis after traveling a distance d. The minimum value of B for which this occurs is B=B0. Therefore, we can express the condition as:
P=k⋅B0
where k is a constant.
7. Finding Additional Conditions:
The particle will also strike the target if the magnetic field is increased. If we set B=2B0, we can find the new pitch:
P′=2πmq(2B0)(v0cosθ)=P2
This implies that the particle will still strike the target if B is doubled.
Conclusion:
The charged particle P will strike the target T if:
1. The magnetic field B=B0.
2. The magnetic field B=2B0.
The charged particle P experiences a magnetic force due to the magnetic field B. The magnetic force F on a charged particle is given by:
F=q(v×B)
where q is the charge of the particle, v is its velocity, and B is the magnetic field.
The velocity v can be resolved into two components:
- vx=v0cosθ (along the x-axis)
- vy=v0sinθ (along the y-axis)
Since the magnetic field B is along the x-axis, the magnetic force will act in the y-direction:
Fy=q(vyB)=q(v0sinθB)
The particle will undergo circular motion in the y-z plane due to the magnetic force. The radius r of the circular motion can be expressed as:
r=mvyqB=m(v0sinθ)qB
The pitch P of the helical path is the distance traveled along the x-axis in one complete revolution. The pitch is given by:
P=2πmqBvx=2πmqB(v0cosθ)
For the particle P to strike the target T on the x-axis, the pitch must be such that the particle returns to the x-axis after traveling a distance d. The minimum value of B for which this occurs is B=B0. Therefore, we can express the condition as:
P=k⋅B0
where k is a constant.
The particle will also strike the target if the magnetic field is increased. If we set B=2B0, we can find the new pitch:
P′=2πmq(2B0)(v0cosθ)=P2
This implies that the particle will still strike the target if B is doubled.
The charged particle P will strike the target T if:
1. The magnetic field B=B0.
2. The magnetic field B=2B0.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA charged particle moving along +ve x-direction with a velocity v enters a region where there is a uniform magnetic field B0(−ˆk),omx=0→x=d. The particle gets deflected at an angle θ from its initial path. The specific charge of the particle is

View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
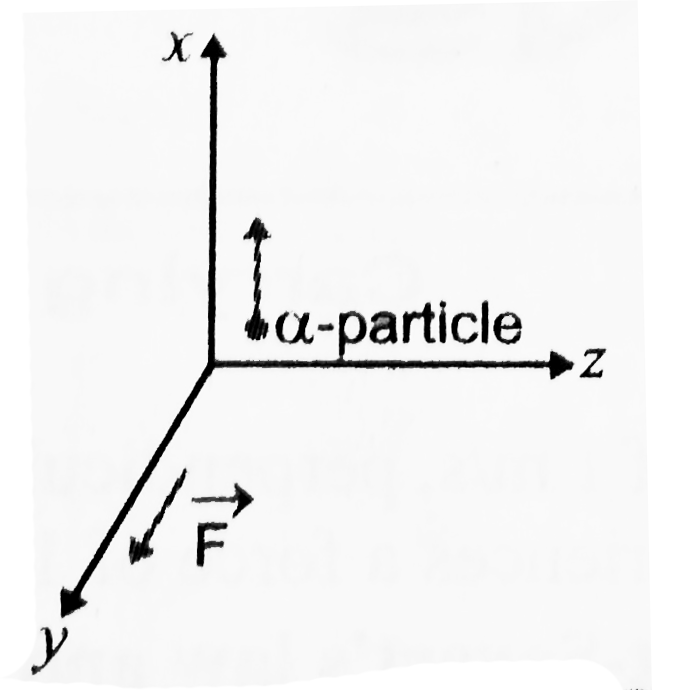
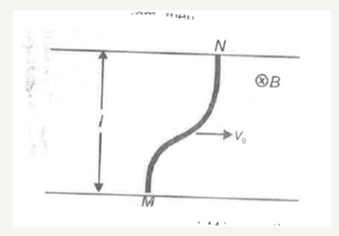
View SolutionA conducting wire MN moves with velocity V_0 along +X-axis in a uniform magnetic field (¯¯¯B=−B0ˆk)as shown in the diagram then
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View Solution
