An electron moves in a circular orbit with a uniform speed v.It produces a magnetic field B at the centre of the circle. The radius of the circle is proportional to
Bv
vB
√vB
√Bv
The correct Answer is:C
To solve the problem of determining the proportionality of the radius of the circular orbit of an electron moving with uniform speed v and producing a magnetic field B at the center of the circle, we can follow these steps:
1. Understanding the Current Produced by the Electron:
- An electron moving in a circular path can be thought of as creating a current. The current I due to a single electron can be expressed as:
I=QT
where Q is the charge of the electron and T is the time period of one complete revolution.
2. Charge of the Electron:
- The charge of an electron is denoted as e. Therefore, we can write:
Q=e
3. Time Period of Circular Motion:
- The time period T for the electron moving in a circle of radius R with speed v is given by:
T=2πRv
4. Substituting for Current:
- Now substituting Q and T into the equation for current:
I=e2πRv=ev2πR
5. Magnetic Field at the Center of the Circular Path:
- The magnetic field B at the center of the circular path due to the current I is given by the formula:
B=μ0I2R
- Substituting the expression for I:
B=μ0(ev2πR)2R=μ0ev4πR
6. Rearranging for Radius R:
- Rearranging the equation to express R in terms of B:
R=μ0ev4πB
7. Identifying Proportionality:
- From the equation R=μ0ev4πB, we can see that the radius R is proportional to the ratio of v to B:
R∝vB
Final Answer:
Thus, the radius R of the circular orbit is proportional to:
R∝vB
- An electron moving in a circular path can be thought of as creating a current. The current I due to a single electron can be expressed as:
I=QT
where Q is the charge of the electron and T is the time period of one complete revolution.
- The charge of an electron is denoted as e. Therefore, we can write:
Q=e
- The time period T for the electron moving in a circle of radius R with speed v is given by:
T=2πRv
- Now substituting Q and T into the equation for current:
I=e2πRv=ev2πR
- The magnetic field B at the center of the circular path due to the current I is given by the formula:
B=μ0I2R
- Substituting the expression for I:
B=μ0(ev2πR)2R=μ0ev4πR
- Rearranging the equation to express R in terms of B:
R=μ0ev4πB
- From the equation R=μ0ev4πB, we can see that the radius R is proportional to the ratio of v to B:
R∝vB
Thus, the radius R of the circular orbit is proportional to:
R∝vB
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
When a particle moves in a circle with a uniform speed
View SolutionAn electron moving in a circular orbit of radius R with frequency f. The magnetic field at the centre of the orbit is
View SolutionThe magnetic field at the centre of dotted circle in the arrangement shown is
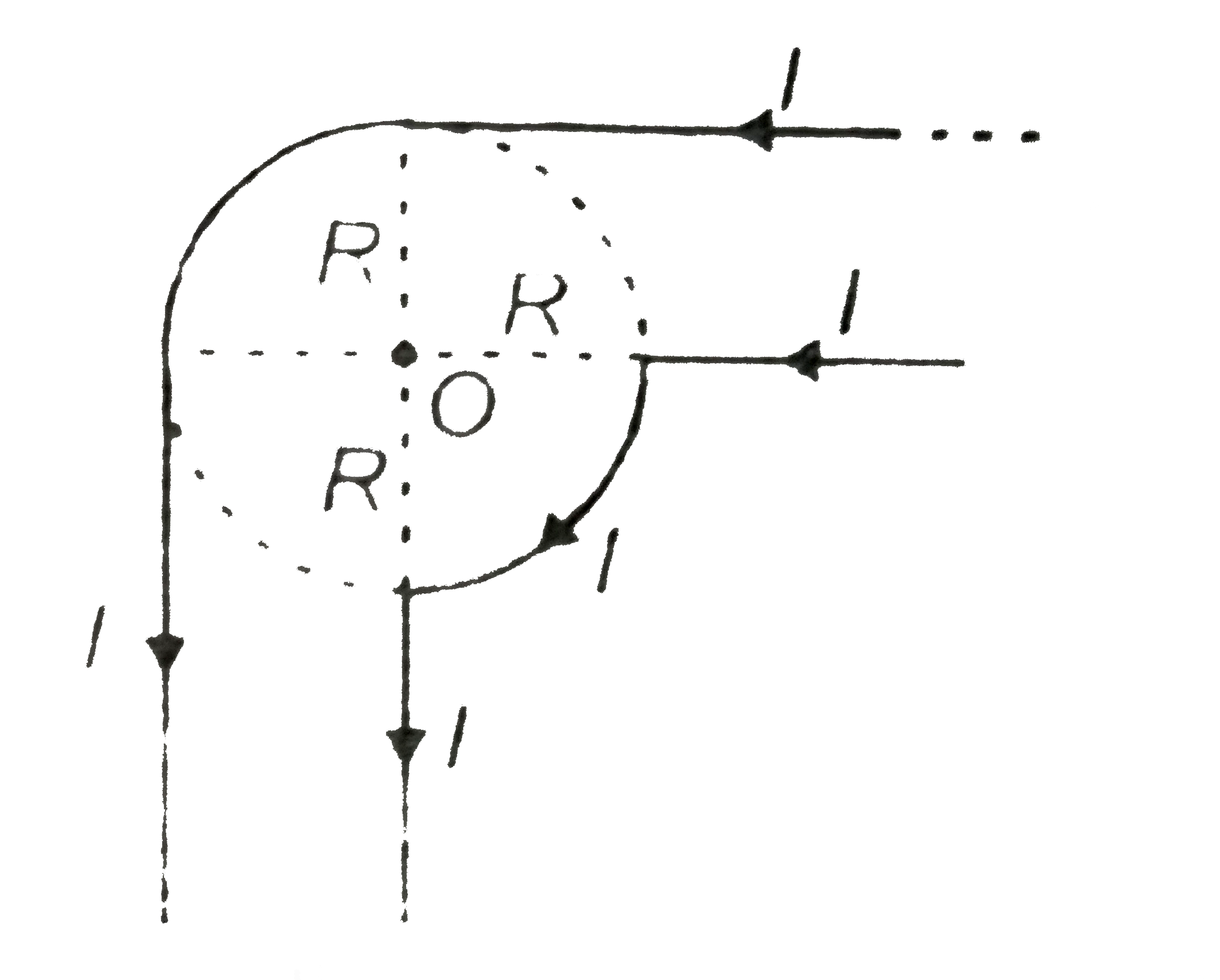
View SolutionAn electron moves in circular orbit of radius r with constant speed v.The force acting in it is
View SolutionAn electron moving in a circular orbit of radius makes n rotations per second. The magnetic field produced at the centre has magnitude :
View SolutionAn electron moving in a circular orbit of radius r makes n rotation per second. The magnetic field produced at the centre has magnitude
View SolutionAn electron is moving on a circular path of radius r with speed v in a transverse magnetic field B. e/m for it will be
View SolutionA proton of mass m and charge q enters a region of uniform magnetic field of a magnitude B with a velocity v directed perpendicular to the magnetic field. It moves in a circular path and leaves the magnetic field after completing a quarter of a circle. The time spent by the proton inside the magnetic field is proportional to:
View SolutionA particle is moving in a circle with uniform speed its motion is
View SolutionAn electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View Solution
